3.5: Double Angle Identities

Learning Objectives

• Use the double angle identities to solve other identities.
• Use the double angle identities to solve equations.

Two special cases of the sum of angles identities arise often enough that we choose to state these identities separately.

IDENTITIES

The double angle identities

\[\sin (2\alpha )=2\sin (\alpha )\cos (\alpha )\]

\[\begin{array}{ccc} {\cos (2\alpha )} & {=} & {\cos ^{2} (\alpha )-\sin ^{2} (\alpha )} \\ {} & {=} & {1-2\sin ^{2} (\alpha )} \\ {} & {=} & {2\cos ^{2} (\alpha )-1} \end{array}\]

These identities follow from the sum of angles identities.

Proof of the sine double angle identity

\[\sin (2\alpha )\nonumber\]
\[=\sin (\alpha +\alpha )\nonumber\]Apply the sum of angles identity
\[=\sin (\alpha )\cos (\alpha )+\cos (\alpha )\sin (\alpha )\nonumber\]Simplify
\[=2\sin (\alpha )\cos (\alpha )\nonumber\]Establishing the identity

Exercise \(\PageIndex{1}\)

Show \(\cos (2\alpha )=\cos ^{2} (\alpha )-\sin ^{2} (\alpha )\) by using the sum of angles identity for cosine.

Answer

\[\begin{array}{l} {\cos \left(2\alpha \right)=\cos (\alpha +\alpha )} \\ {\cos (\alpha )\cos (\alpha )-\sin (\alpha )\sin (\alpha )} \\ {\cos ^{2} (\alpha )-\sin ^{2} (\alpha )} \end{array}\nonumber\]

For the cosine double angle identity, there are three forms of the identity stated because the basic form, \(\cos (2\alpha )=\cos ^{2} (\alpha )-\sin ^{2} (\alpha )\), can be rewritten using the Pythagorean Identity. Rearranging the Pythagorean Identity results in the equality \(\cos ^{2} (\alpha )=1-\sin ^{2} (\alpha )\), and by substituting this into the basic double angle identity, we obtain the second form of the double angle identity.

\[\cos (2\alpha )=\cos ^{2} (\alpha )-\sin ^{2} (\alpha )\nonumber\]Substituting using the Pythagorean identity
\[\cos (2\alpha )=1-\sin ^{2} (\alpha )-\sin ^{2} (\alpha )\nonumber\]Simplifying
\[\cos (2\alpha )=1-2\sin ^{2} (\alpha )\nonumber\]

Example \(\PageIndex{1}\)

If \(\sin (\theta )=\dfrac{3}{5}\) and \(\theta\) is in the second quadrant, find exact values for \(\sin (2\theta )\) and \(\cos (2\theta )\).

Solution

To evaluate \(\cos (2\theta )\), since we know the value for \(\sin (\theta )\) we can use the version of the double angle that only involves sine.

\[\cos (2\theta )=1-2\sin ^{2} (\theta )=1-2\left(\dfrac{3}{5} \right)^{2} =1-\dfrac{18}{25} =\dfrac{7}{25}\nonumber\]

Since the double angle for sine involves both sine and cosine, we’ll need to first find \(\cos (\theta )\), which we can do using the Pythagorean Identity.

\[\sin ^{2} (\theta )+\cos ^{2} (\theta )=1\nonumber\]
\[\left(\dfrac{3}{5} \right)^{2} +\cos ^{2} (\theta )=1\nonumber\]
\[\cos ^{2} (\theta )=1-\dfrac{9}{25}\nonumber\]
\[\cos (\theta )=\pm \sqrt{\dfrac{16}{25} } =\pm \dfrac{4}{5}\nonumber\]

Since \(\theta\) is in the second quadrant, we know that cos( \(\theta\)) \(\mathrm{<}\) 0, so

\[\cos (\theta )=-\dfrac{4}{5}\nonumber\]

Now we can evaluate the sine double angle

\[\sin (2\theta )=2\sin (\theta )\cos (\theta )=2\left(\dfrac{3}{5} \right)\left(-\dfrac{4}{5} \right)=-\dfrac{24}{25}\nonumber\]

Example \(\PageIndex{2}\)

Simplify the expressions

a) \(2\cos ^{2} \left(12{}^\circ \right)-1\)

b) \(8\sin \left(3x\right)\cos \left(3x\right)\)

Solution

a) Notice that the expression is in the same form as one version of the double angle identity for cosine: \(\cos (2\theta )=2\cos ^{2} (\theta )-1\). Using this,

\[2\cos ^{2} \left(12{}^\circ \right)-1=\cos \left(2\cdot 12{}^\circ \right)=\cos \left(24{}^\circ \right)\nonumber\]

b) This expression looks similar to the result of the double angle identity for sine.

\[8\sin \left(3x\right)\cos \left(3x\right)\nonumber\]Factoring a 4 out of the original expression
\[4\cdot 2\sin \left(3x\right)\cos \left(3x\right)\nonumber\]Applying the double angle identity
\[4\sin (6x)\nonumber\]

We can use the double angle identities to simplify expressions and prove identities.

Example \(\PageIndex{3}\)

Simplify \(\dfrac{\cos (2t)}{\cos (t)-\sin (t)}\).

Solution

With three choices for how to rewrite the double angle, we need to consider which will be the most useful. To simplify this expression, it would be great if the denominator would cancel with something in the numerator, which would require a factor of \(\cos (t)-\sin (t)\) in the numerator, which is most likely to occur if we rewrite the numerator with a mix of sine and cosine.

\[\dfrac{\cos (2t)}{\cos (t)-\sin (t)}\nonumber\]Apply the double angle identity
\[=\dfrac{\cos ^{2} (t)-\sin ^{2} (t)}{\cos (t)-\sin (t)}\nonumber\]Factor the numerator
\[=\dfrac{\left(\cos (t)-\sin (t)\right)\left(\cos (t)+\sin (t)\right)}{\cos (t)-\sin (t)}\nonumber\]Cancelling the common factor
\[=\cos (t)+\sin (t)\nonumber\]Resulting in the most simplified form

Example \(\PageIndex{4}\)

Prove \(\sec (2\alpha )=\dfrac{\sec ^{2} (\alpha )}{2-\sec ^{2} (\alpha )}\).

Solution

Since the right side seems a bit more complicated than the left side, we begin there.

\[\dfrac{\sec ^{2} (\alpha )}{2-\sec ^{2} (\alpha )}\nonumber\]Rewrite the secants in terms of cosine
\[=\dfrac{\dfrac{1}{\cos ^{2} (\alpha )} }{2-\dfrac{1}{\cos ^{2} (\alpha )} }\nonumber\]

At this point, we could rewrite the bottom with common denominators, subtract the terms, invert and multiply, then simplify. Alternatively, we can multiple both the top and bottom by \(\cos ^{2} (\alpha )\), the common denominator:

\[=\dfrac{\dfrac{1}{\cos ^{2} (\alpha )} \cdot \cos ^{2} (\alpha )}{\left(2-\dfrac{1}{\cos ^{2} (\alpha )} \right)\cdot \cos ^{2} (\alpha )}\nonumber\]Distribute on the bottom
\[=\dfrac{\dfrac{\cos ^{2} (\alpha )}{\cos ^{2} (\alpha )} }{2\cos ^{2} (\alpha )-\dfrac{\cos ^{2} (\alpha )}{\cos ^{2} (\alpha )} \cdot }\nonumber\]Simplify
\[=\dfrac{1}{2\cos ^{2} (\alpha )-1}\nonumber\]Rewrite the denominator as a double angle
\[=\dfrac{1}{\cos (2\alpha )}\nonumber\]Rewrite as a secant
\[=\sec (2\alpha )\nonumber\]Establishing the identity

Exercise \(\PageIndex{2}\)

Use an identity to find the exact value of \(\cos ^{2} \left(75{}^\circ \right)-\sin ^{2} \left(75{}^\circ \right)\).

Answer

\[\cos ^{2} \left(75{}^\circ \right)-\sin ^{2} \left(75{}^\circ \right)=\cos (2\cdot 75{}^\circ )\nonumber\] \[ = \cos (150{}^\circ )=\dfrac{-\sqrt{3} }{2}\nonumber\]

As with other identities, we can also use the double angle identities for solving equations.

Example \(\PageIndex{5}\)

Solve \(\cos (2t)=\cos (t)\) for all solutions with \(0\le t<2\pi\).

Solution

In general when solving trig equations, it makes things more complicated when we have a mix of sines and cosines and when we have a mix of functions with different periods. In this case, we can use a double angle identity to rewrite the cos(2t). When choosing which form of the double angle identity to use, we notice that we have a cosine on the right side of the equation. We try to limit our equation to one trig function, which we can do by choosing the version of the double angle formula for cosine that only involves cosine.

\[\cos (2t)=\cos (t)\nonumber\]Apply the double angle identity
\[2\cos ^{2} (t)-1=\cos (t)\nonumber\]This is quadratic in cosine, so make one side 0
\[2\cos ^{2} (t)-\cos (t)-1=0\nonumber\]Factor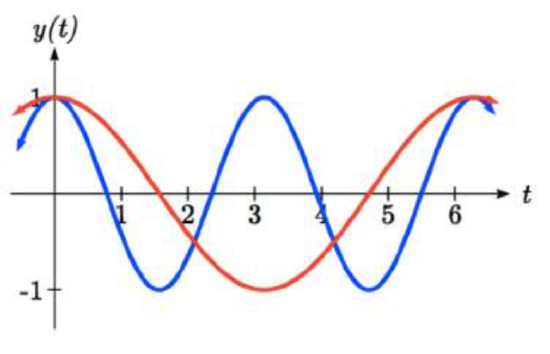
\[\left(2\cos (t)+1\right)\left(\cos (t)-1\right)=0\nonumber\]Break this apart to solve each part separately

\[2\cos (t)+1=0\text{ or }\cos (t)-1=0\nonumber\]
\[\cos (t)=-\dfrac{1}{2}\text{ or }\cos (t)=1\nonumber\]
\[t=\dfrac{2\pi }{3}\text{ or }t=\dfrac{4\pi }{3}\text{ or }t=0\nonumber\]

Looking at a graph of cos(2t) and cos(t) shown together, we can verify that these three solutions on [0, 2 \(\pi\)) seem reasonable.

Important Topics of This Section

• Double angle identity
• Using identities
• Simplify equations
• Prove identities
• Solve equations