4.4: Applications

Learning Objectives

• Apply inverse trigonometric functions to real-life situations.

Throughout its early development, trigonometry was often used as a means of indirect measurement, e.g. determining large distances or lengths by using measurements of angles and small, known distances. Today, trigonometry is widely used in physics, astronomy, engineering, navigation, surveying, and various fields of mathematics and other disciplines. In this section we will see some of the ways in which trigonometry can be applied. Your calculator should be in degree mode for these examples.

Example 4.4.1

A person stands $150$ ft away from a flagpole and measures an angle of elevation of $32^\circ$ from his horizontal line of sight to the top of the flagpole. Assume that the person's eyes are a vertical distance of 6 ft from the ground. What is the height of the flagpole?

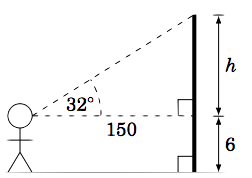
Solution:

The picture on the right describes the situation. We see that the height of the flagpole is $h + 6$ ft, where

$$\frac{h}{150} ~=~ \tan\;32^\circ \quad\Rightarrow\quad h ~=~ 150\;\tan\;32^\circ ~=~ 150\;(0.6249) ~=~ 94 ~.$$

How did we know that $\tan\;32^\circ = 0.6249\,$? By using a calculator. And since none of the numbers we were given had decimal places, we rounded off the answer for $h$ to the nearest integer. Thus, the height of the flagpole is $\,h + 6 = 94 + 6 = \boxed{100 ~\text{ft}}$.

Example 4.4.2

A person standing $400$ ft from the base of a mountain measures the angle of elevation from the ground to the top of the mountain to be $25^\circ$. The person then walks $500$ ft straight back and measures the angle of elevation to now be $20^\circ$. How tall is the mountain?

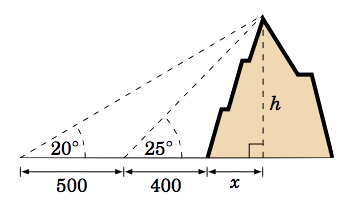
Solution:

We will assume that the ground is flat and not inclined relative to the base of the mountain. Let $h$ be the height of the mountain, and let $x$ be the distance from the base of the mountain to the point directly beneath the top of the mountain, as in the picture on the right. Then we see that

$$\begin{align} \frac{h}{x + 400} ~=~ \tan\;25^\circ \quad &\Rightarrow \quad h ~=~ (x + 400)\;\tan\;25^\circ ~,~\text{and}\\ \frac{h}{x + 400 + 500} ~=~ \tan\;20^\circ \quad &\Rightarrow \quad h ~=~ (x + 900)\;\tan\;20^\circ ~,~\text{so} \end{align}$$

$(x + 400)\;\tan\;25^\circ ~=~ (x + 900)\;\tan\;20^\circ$, since they both equal $h$. Use that equation to solve for $x$:

$$x\;\tan\;25^\circ ~-~ x\;\tan\;20^\circ ~=~ 900\;\tan\;20^\circ ~-~ 400\;\tan\;25^\circ \quad\Rightarrow\quad x ~=~ \frac{900\;\tan\;20^\circ ~-~ 400\;\tan\;25^\circ}{\tan\;25^\circ ~-~ \tan\;20^\circ} ~=~ 1378~ \text{ft}$$

Finally, substitute $x$ into the first formula for $h$ to get the height of the mountain:

$$h ~=~ (1378 + 400)\;\tan\;25^\circ ~=~ 1778\;(0.4663) ~=~ \boxed{829~ \text{ft}}$$

Example 4.4.3

A blimp $4280$ ft above the ground measures an angle of depression of $24^\circ$ from its horizontal line of sight to the base of a house on the ground. Assuming the ground is flat, how far away along the ground is the house from the blimp?

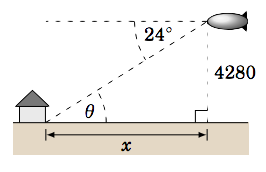
Solution:

Let $x$ be the distance along the ground from the blimp to the house, as in the picture to the right. Since the ground and the blimp's horizontal line of sight are parallel, we know from elementary geometry that the angle of elevation $\theta$ from the base of the house to the blimp is equal to the angle of depression from the blimp to the base of the house, i.e. $\theta = 24^\circ$. Hence,

$$\frac{4280}{x} ~=~ \tan\;24^\circ \quad\Rightarrow\quad x ~=~ \frac{4280}{\tan\;24^\circ} ~=~ \boxed{9613 ~\text{ft}}~.$$

Example 4.4.4

An observer at the top of a mountain $3$ miles above sea level measures an angle of depression of $2.23^\circ$ to the ocean horizon. Use this to estimate the radius of the earth.

Figure 4.4.1

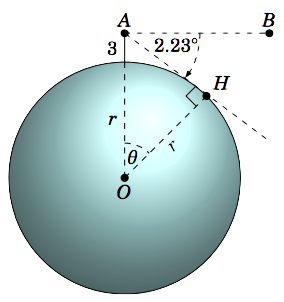
Solution:

We will assume that the earth is a sphere. Let $r$ be the radius of the earth. Let the point $A$ represent the top of the mountain, and let $H$ be the ocean horizon in the line of sight from $A$, as in Figure 1.3.1. Let $O$ be the center of the earth, and let $B$ be a point on the horizontal line of sight from $A$ (i.e. on the line perpendicular to $\overline{OA}$). Let $\theta$ be the angle $\angle\,AOH$.

Since $A$ is $3$ miles above sea level, we have $OA = r + 3$. Also, $OH = r$. Now sincev$\overline{AB} \perp \overline{OA}$, we have $\angle\,OAB = 90^\circ$, so we see that $\angle\,OAH = 90^\circ - 2.23^\circ = 87.77^\circ$. We see that the line through $A$ and $H$ is a tangent line to the surface of the earth (considering the surface as the circle of radius $r$ through $H$ as in the picture). So by Exercise 14 in Section 1.1, $\overline{AH} \perp \overline{OH}$ and hence $\angle\,OHA = 90^\circ$. Since the angles in the triangle $\triangle\,OAH$ add up to $180^\circ$, we have $\theta = 180^\circ - 90^\circ - 87.77^\circ = 2.23^\circ$. Thus,

$$\cos\;\theta ~=~ \frac{OH}{OA} ~=~ \frac{r}{r+3} \quad\Rightarrow\quad \frac{r}{r+3} ~=~ \cos\;2.23^\circ ~,$$

so solving for $r$ we get

$$\begin{align} r ~=~ (r ~+~ 3)\;\cos\;2.23^\circ \quad &\Rightarrow \quad r ~-~ r\;\cos\;2.23^\circ ~=~ 3\;\cos\;2.23^\circ\\[4pt] &\Rightarrow \quad r ~=~ \frac{3\;\cos\;2.23^\circ}{1 ~-~ \cos\;2.23^\circ}\\ &\Rightarrow \quad \boxed{r ~=~ 3958.3 ~\text{miles}} ~. \end{align}$$

Note: This answer is very close to the earth's actual (mean) radius of $3956.6$ miles.

Example 4.4.5

As another application of trigonometry to astronomy, we will find the distance from the earth to the sun. Let $O$ be the center of the earth, let $A$ be a point on the equator, and let $B$ represent an object (e.g. a star) in space, as in the picture on the right. If the earth is positioned in such a way that the angle $\angle\,OAB = 90^\circ$, then we say that the angle $\alpha = \angle\,OBA$ is the equatorial parallax of the object. The equatorial parallax of the sun has been observed to be approximately $\alpha =0.00244^\circ$. Use this to estimate the distance from the center of the earth to the sun.

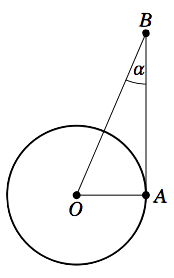
Solution:

Let $B$ be the position of the sun. We want to find the length of $\overline{OB}$. We will use the actual radius of the earth, mentioned at the end of Example 1.14, to get $OA = 3956.6$ miles. Since $\angle\,OAB = 90^\circ$, we have

$$\frac{OA}{OB} ~=~ \sin\;\alpha \quad\Rightarrow\quad OB ~=~ \frac{OA}{\sin\;\alpha} ~=~ \frac{3956.6}{\sin\;0.00244^\circ} ~=~ 92908394 ~,$$

so the distance from the center of the earth to the sun is approximately $\fbox{\(93\) million miles}~.$

Note: The earth's orbit around the sun is an ellipse, so the actual distance to the sun varies.

In the above example we used a very small angle ($0.00244^\circ$). A degree can be divided into smaller units: a minute is one-sixtieth of a degree, and a second is one-sixtieth of a minute. The symbol for a minute is $'$ and the symbol for a second is $''$. For example, $4.5^\circ = 4^\circ\;30'$. And $4.505^\circ = 4^\circ\;30'\;18''$:

$$4^\circ\;30'\;18'' ~=~ 4 ~+~ \frac{30}{60} ~+~ \frac{18}{3600} ~\text{degrees} ~=~ 4.505^\circ$$

In Example 1.15 we used $\alpha = 0.00244^\circ \approx 8.8''$, which we mention only because some angle measurement devices do use minutes and seconds.

Example 4.4.6

An observer on earth measures an angle of $32'\;4''$ from one visible edge of the sun to the other (opposite) edge, as in the picture on the right. Use this to estimate the radius of the sun.

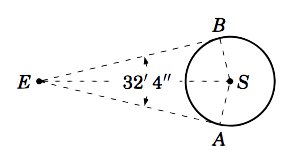
Solution:

Let the point $E$ be the earth and let $S$ be the center of the sun. The observer's lines of sight to the visible edges of the sun are tangent lines to the sun's surface at the points $A$ and $B$. Thus, $\angle\,EAS = \angle\,EBS = 90^\circ$. The radius of the sun equals $AS$. Clearly $AS = BS$. So since $EB = EA$ (why?), the triangles $\triangle\,EAS$ and $\triangle\,EBS$ are similar. Thus, $\angle\,AES = \angle\,BES = \frac{1}{2}\; \angle\,AEB = \frac{1}{2}\;(32'\;4'') = 16'\;2'' = (16/60) + (2/3600) = 0.26722^\circ$.

Now, $ES$ is the distance from the surface of the earth (where the observer stands) to the center of the sun. In Example 1.15 we found the distance from the center of the earth to the sun to be $92,908,394$ miles. Since we treated the sun in that example as a point, then we are justified in treating that distance as the distance between the centers of the earth and sun. So $ES = 92908394 - ~\text{radius of earth} = 92908394 - 3956.6 = 92904437.4$ miles. Hence,

$$\sin\;(\angle\,AES) ~=~ \frac{AS}{ES} \quad\Rightarrow\quad AS ~=~ ES \;\sin\;0.26722^\circ ~=~ (92904437.4)\;\sin\;0.26722^\circ ~=~ \boxed{433,293 ~\text{miles}} ~.$$

Note: This answer is close to the sun's actual (mean) radius of $432,200$ miles.

You may have noticed that the solutions to the examples we have shown required at least one right triangle. In applied problems it is not always obvious which right triangle to use, which is why these sorts of problems can be difficult. Often no right triangle will be immediately evident, so you will have to create one. There is no general strategy for this, but remember that a right triangle requires a right angle, so look for places where you can form perpendicular line segments. When the problem contains a circle, you can create right angles by using the perpendicularity of the tangent line to the circle at a point with the line that joins that point to the center of the circle.

For some problems, it may help to remember that when a right triangle has a hypotenuse of length $r$ and an acute angle $\theta$, as in the picture below, the adjacent side will have length $r\,\cos\;\theta$ and the opposite side will have length $r\,\sin\;\theta$. You can think of those lengths as the horizontal and vertical ``components'' of the hypotenuse.

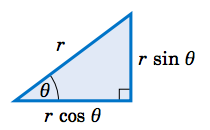
Notice in the above right triangle that we were given two pieces of information: one of the acute angles and the length of the hypotenuse. From this we determined the lengths of the other two sides, and the other acute angle is just the complement of the known acute angle. In general, a triangle has six parts: three sides and three angles. Solving a triangle means finding the unknown parts based on the known parts. In the case of a right triangle, one part is always known: one of the angles is $90^\circ$.

Example 4.4.7

Solve the right triangle in Figure 4.4.2 using the given information:

Figure 4.4.2

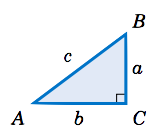
(a) $c = 10,\, A = 22^◦$
Solution: The unknown parts are $a$, $b$, and $B$. Solving yields:

$$\begin{align} a ~ &= ~ c\;\sin\;A ~ &= ~ 10\;\sin\;22^\circ ~ &= ~ 3.75\\ b ~ &= ~ c\;\cos\;A ~ &= ~ 10\;\cos\;22^\circ ~ &= ~ 9.27\\ B ~ &= ~ 90^\circ ~-~ A ~ &= ~ 90^\circ ~-~ 22^\circ ~ &= ~ 68^\circ \end{align}$$

(b) $b = 8,\, A = 40^◦$
Solution: The unknown parts are $a$, $c$, and $B$. Solving yields:

$$\begin{align} \frac{a}{b} ~ &= ~ \tan\;A \quad &\Rightarrow \quad a ~ &= ~ b\;\tan\;A ~ = ~ 8\;\tan\;40^\circ ~ = ~ 6.71\\[2mm] \frac{b}{c} ~ &= ~ \cos\;A \quad &\Rightarrow \quad c ~ &= ~ \frac{b}{\cos\;A} ~ = ~ \frac{8}{\cos\;40^\circ} ~ = ~ 10.44 \end{align}$$

(c) $a = 3,\, b = 4$
Solution: The unknown parts are $c$, $A$, and $B$. By the Pythagorean Theorem,

$$c ~=~ \sqrt{a^2 ~+~ b^2} ~=~ \sqrt{3^2 ~+~ 4^2} ~=~ \sqrt{25} ~=~ 5 ~.$$

Now, $\tan\;A = \frac{a}{b} = \frac{3}{4} = 0.75$. So how do we find $A$? There should be a key labeled $\fbox{\(\tan^{-1}\)}$ on your calculator, which works like this: give it a number $x$ and it will tell you the angle $\theta$ such that $\tan\;\theta = x$. In our case, we want the angle $A$ such that $\tan\;A = 0.75$:

$$\text{Enter: } 0.75 \quad \text{Press:}\fbox{\(\tan^{-1}\)} \quad \text{Answer: } 36.86989765$$

This tells us that $A = 36.87^\circ$, approximately. Thus $B = 90^\circ - A = 90^\circ - 36.87^\circ = 53.13^\circ$.

Note: The $\fbox{ \(\sin^{-1}\)}$ and $\fbox{ \(\cos^{-1}\)}$ keys work similarly for sine and cosine, respectively. These keys use the inverse trigonometric functions, which we will discuss in Chapter 5.

Contributors and Attributions

• Michael Corral (Schoolcraft College). The content of this page is distributed under the terms of the GNU Free Documentation License, Version 1.2.