3.4: Proving Lines and Angles Equal
- Last updated
- Jul 1, 2021
- Save as PDF
- Page ID
- 72145
( \newcommand{\kernel}{\mathrm{null}\,}\)
We can prove lines and angles equal if we can show they are corresponding parts of congruent triangles, We find it convenient to present these proofs in double-column form with statements in the left columnand the reason for each statement in the right.
Example
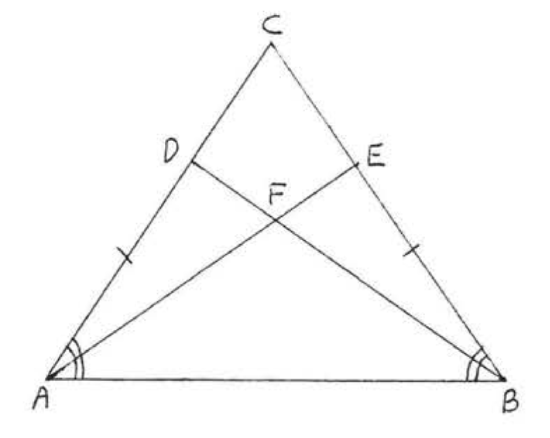
Given
Solution
| Statements | Reasons |
| 1. |
1. Given. |
| 2. |
2. Alternate interior angles of parallel lines |
| 3. |
3. Identity. |
| 4. |
4. |
| 5. |
5. Corresponding sides of congruent triangles are equal, |
Explanation: Each of the first three statements says that a side or angle of
Reasons Lines Are Equal
- Given. This means we are asked to assume the lines are equal at the beginning of the exercise, For example, the problem will state "given
- Identity. This means the identical line segment appears in both triangles, For example,
Reasons Angles Are Equal
- Given.
- Identity.
- Alternate interior angles of parallel lines are equal. To apply this reason we must be given that the lines are parallel.
- Corresponding angles of parallel lines equal.
- Vertical angles are equal.
These are not the only possible reasons but they are all that we will use at first.
We should also select the three pairs of equal sides or angles so that one of the reasons
Statement 5 is the one we wish to prove, The reason is that corresponding sides (or angles) of congruent triangles are equal. Wecan use this reason here because the triangles have already been proven congruent in statement 4,
One final comment, Notice how the solution of Example
Let us give another example:
Example
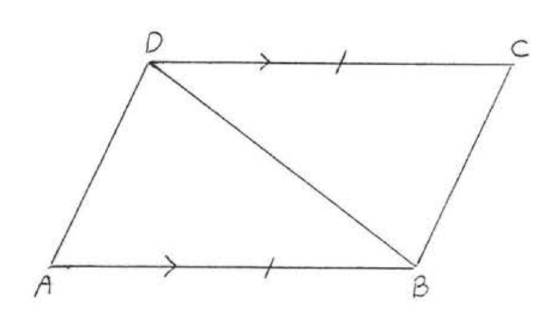
Given
Solution
| Statements | Reasons |
| 1. |
1. Given. |
| 2. |
2. Alternate interior angles of parallel lines ( |
| 3. |
3. Vertical angles are equal. |
| 4. |
4. |
| 5. |
5. Corresponding sides of congruent triangles are equal, |
Problems
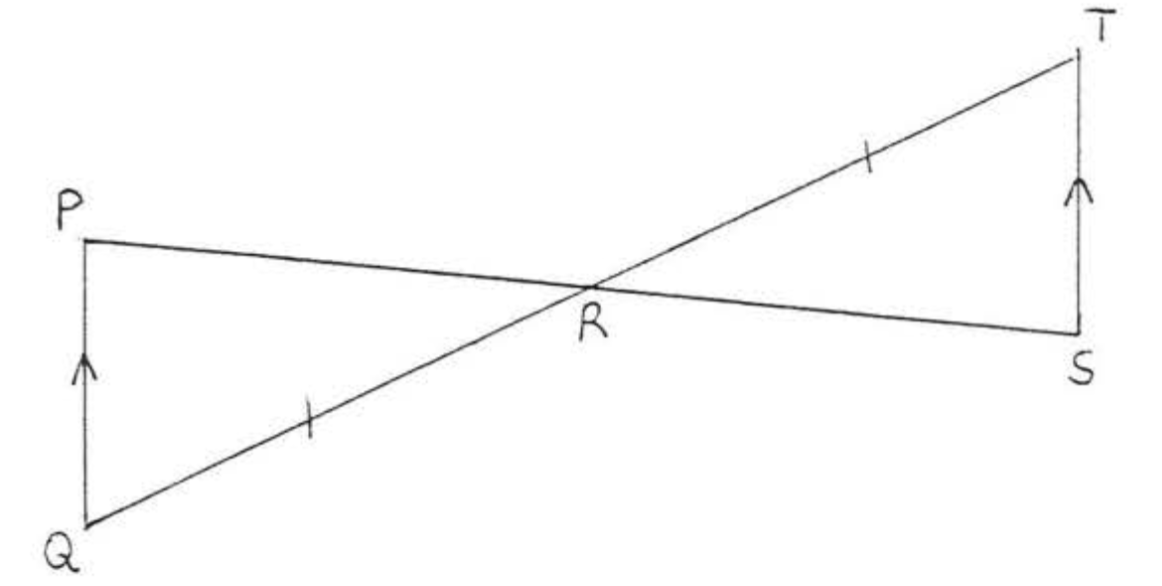
1. Given
2. Given
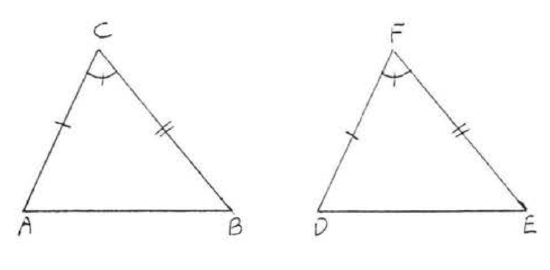
3. Given
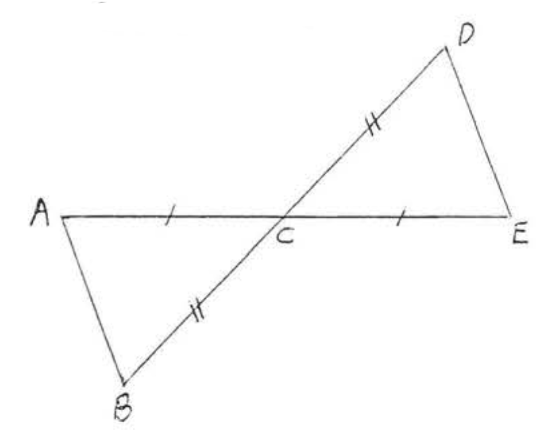
4. Given
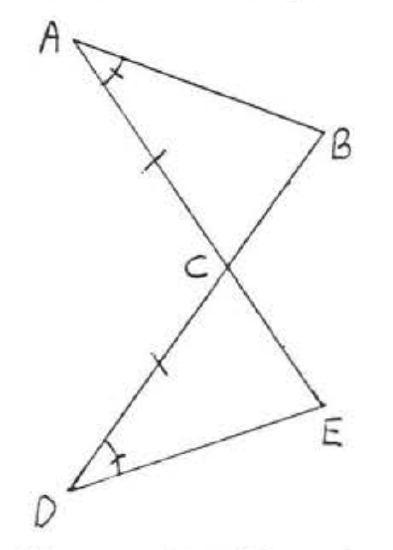
5. Given
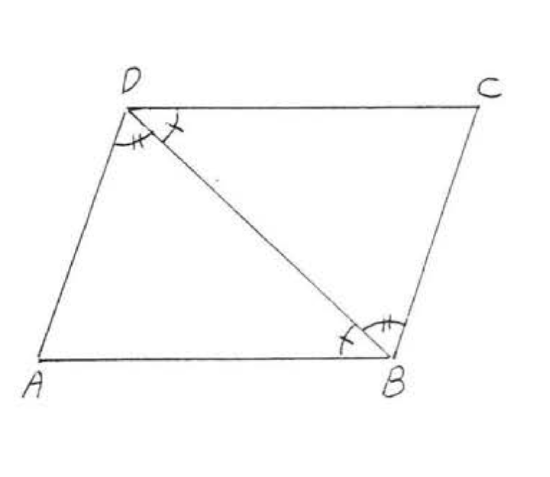
6. Given
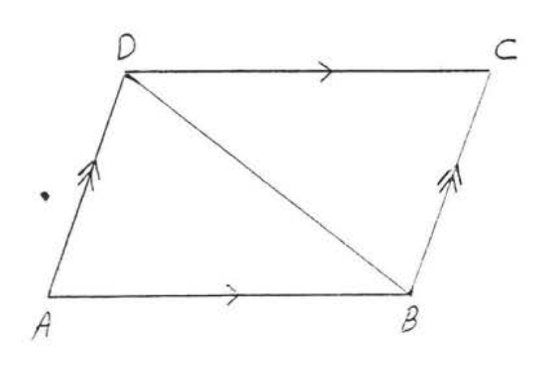
7. Given
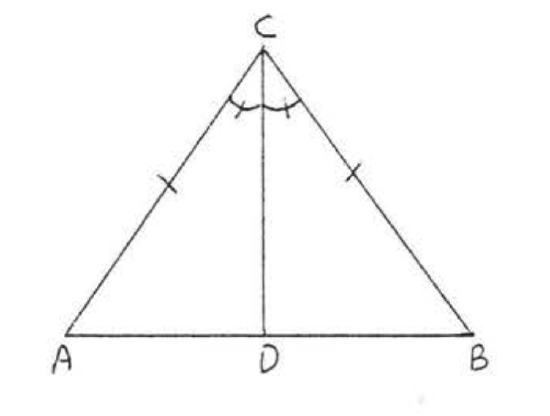
8. Given
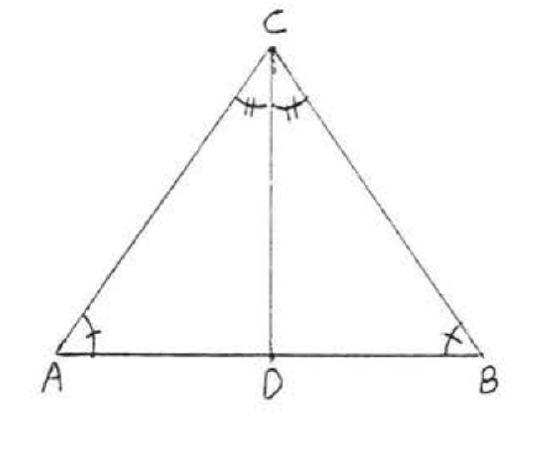
9. Given
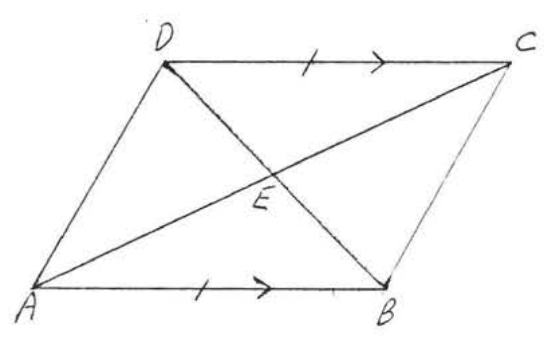
10. Given
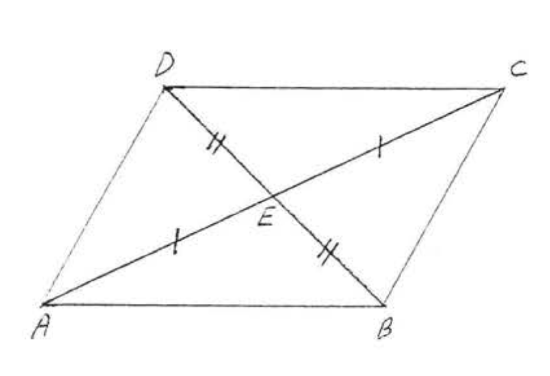
11. Given
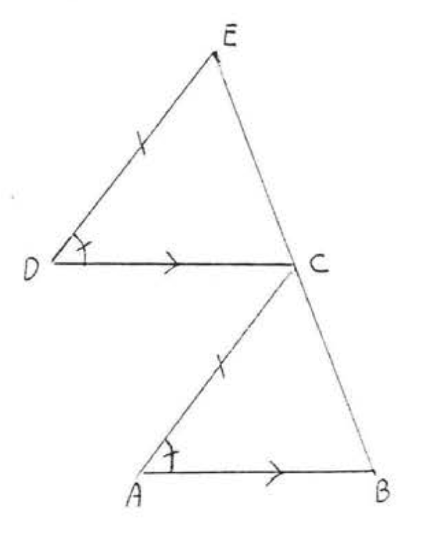
12. Given
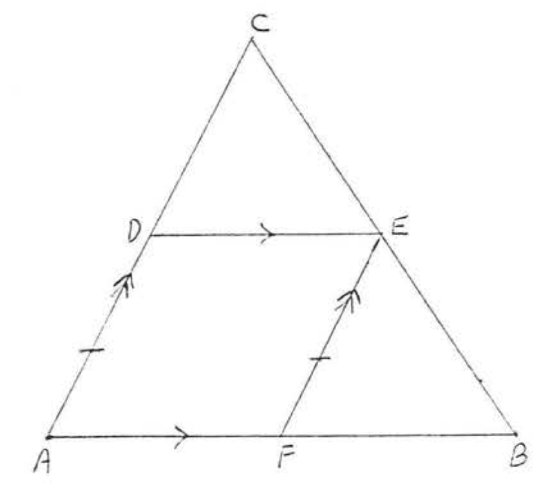
13. Given
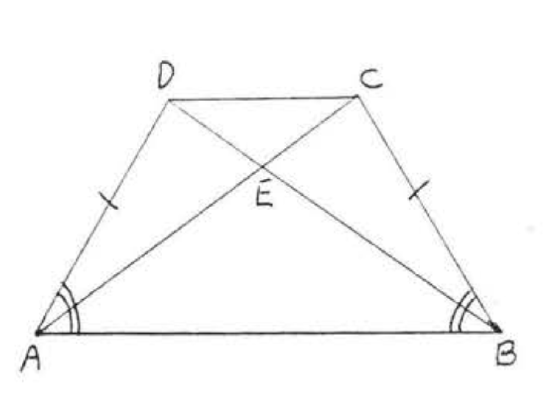
14. Given