4.3: Inverse Trigonometric Properties

Learning Objectives

• Relate the concept of inverse functions to trigonometric functions.
• Reduce the composite function to an algebraic expression involving no trigonometric functions.
• Use the inverse reciprocal properties.
• Compose each of the six basic trigonometric functions with \(\tan^{-1}(x)\).

Evaluating Compositions of the Form \(f^{-1}(g(x))\)

Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form \(f^{-1}(g(x))\). For special values of \(x\),we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is \(\theta\), making the other \(\dfrac{\pi}{2}−\theta\).Consider the sine and cosine of each angle of the right triangle in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Right triangle illustrating the cofunction relationships

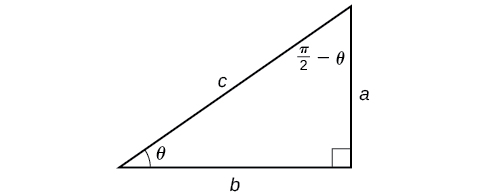
Because \(\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)\), we have \({\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta\) if \(0≤\theta≤\pi\). If \(\theta\) is not in this domain, then we need to find another angle that has the same cosine as \(\theta\) and does belong to the restricted domain; we then subtract this angle from \(\dfrac{\pi}{2}\).Similarly, \(\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)\), so \({\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta\) if \(−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}\). These are just the function-cofunction relationships presented in another way.

Given functions of the form \({\sin}^{−1}(\cos x)\) and \({\cos}^{−1}(\sin x)\), evaluate them.

1. If \(x\) is in \([ 0,\pi ]\), then \({\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x\).
2. If \(x\) is not in \([ 0,\pi ]\), then find another angle \(y\) in \([ 0,\pi ]\) such that \(\cos y=\cos x\).

   \[{\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y\]

3. If \(x\) is in \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), then \({\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x\).
4. If \(x\) is not in \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), then find another angle \(y\) in \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\) such that \(\sin y=\sin x\).

   \[{\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y\]

Example \(\PageIndex{1}\): Evaluating the Composition of an Inverse Sine with a Cosine

Evaluate \({\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)\)

1. by direct evaluation.
2. by the method described previously.

Solution

1. Here, we can directly evaluate the inside of the composition. \[\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}\] Now, we can evaluate the inverse function as we did earlier. \[{\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}\]
2. We have \(x=\dfrac{13\pi}{6}\), \(y=\dfrac{\pi}{6}\), and \[\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}\]

Exercise \(\PageIndex{1}\)

Evaluate \({\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )\).

Answer

\(\dfrac{3\pi}{4}\)

Evaluating Compositions of the Form \(f(g^{−1}(x))\)

To evaluate compositions of the form \(f(g^{−1}(x))\), where \(f\) and \(g\) are any two of the functions sine, cosine, or tangent and \(x\) is any input in the domain of \(g^{−1}\), we have exact formulas, such as \(\sin({\cos}^{−1}x)=\sqrt{1−x^2}\). When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, \({\sin}^2 x+{\cos}^2 x=1\), to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.

Example \(\PageIndex{2}\): Evaluating the Composition of a Sine with an Inverse Cosine

Find an exact value for \(\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)\).

Solution

Beginning with the inside, we can say there is some angle such that \(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\), which means \(\cos \theta=\dfrac{4}{5}\), and we are looking for \(\sin \theta\). We can use the Pythagorean identity to do this.

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}\]

Since \(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\) is in quadrant I, \(\sin \theta\) must be positive, so the solution is \(35\). See Figure \(\PageIndex{11}\).

Figure \(\PageIndex{11}\): Right triangle illustrating that if \(\cos \theta=\dfrac{4}{5}\), then \(\sin \theta=\dfrac{3}{5}\)

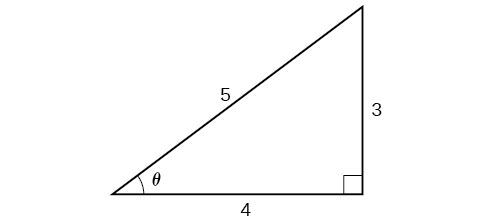
We know that the inverse cosine always gives an angle on the interval \([ 0,\pi ]\), so we know that the sine of that angle must be positive; therefore \(\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}\).

Exercise \(\PageIndex{2}\)

Evaluate \(\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )\).

Answer

\(\frac{12}{13}\)

Example \(\PageIndex{3}\): Evaluating the Composition of a Sine with an Inverse Tangent

Find an exact value for \(\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)\).

Solution

While we could use a similar technique as in Example \(\PageIndex{6}\), we will demonstrate a different technique here. From the inside, we know there is an angle such that \(\tan \theta=\dfrac{7}{4}\). We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure \(\PageIndex{12}\).

Figure \(\PageIndex{12}\): A right triangle with two sides known

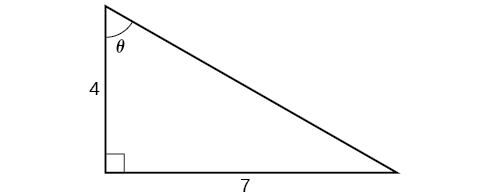
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.

\[\begin{align*}
4^2+7^2&= {hypotenuse}^2\\
hypotenuse&=\sqrt{65}\\
\text {Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.}\\
\sin \theta&= \dfrac{7}{\sqrt{65}}\\
\text {This gives us our desired composition.}\\
\sin \left ({\tan}^{-1} \left (\dfrac{7}{4} \right ) \right )&= \sin \theta\\
&= \dfrac{7}{\sqrt{65}}\\
&= \dfrac{7\sqrt{65}}{65}
\end{align*}\]

Exercise \(\PageIndex{3}\)

Evaluate \(\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)\).

Answer

\(\dfrac{4\sqrt{2}}{9}\)

Example \(\PageIndex{4}\): Finding the Cosine of the Inverse Sine of an Algebraic Expression

Find a simplified expression for \(\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)\) for \(−3≤x≤3\).

Solution

We know there is an angle \(\theta\) such that \(\sin \theta=\dfrac{x}{3}\).

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}\]

Because we know that the inverse sine must give an angle on the interval \([ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]\), we can deduce that the cosine of that angle must be positive.

\(cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}\)

Exercise \(\PageIndex{4}\)

Find a simplified expression for \(\sin({\tan}^{−1}(4x))\) for \(−\dfrac{1}{4}≤x≤\dfrac{1}{4}\).

Answer

\(\dfrac{4x}{\sqrt{16x^2+1}}\)

Key Concepts

• If the inside function is a trigonometric function, then the only possible combinations are \({\sin}^{−1}(\cos x)=\frac{\pi}{2}−x\) if \(0≤x≤\pi\) and \({\cos}^{−1}(\sin x)=\frac{\pi}{2}−x\) if \(−\frac{\pi}{2}≤x≤\frac{\pi}{2}\). See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function. See Example \(\PageIndex{3}\).
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides. See Example \(\PageIndex{4}\).

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.