14.5: Coding Theory, Group Codes

Transmission Problem

In this section, we will introduce the basic ideas involved in coding theory and consider solutions of a coding problem by means of group codes.

Imagine a situation in which information is being transmitted between two points. The information takes the form of high and low pulses (for example, radio waves or electric currents), which we will label 1 and 0, respectively. As these pulses are sent and received, they are grouped together in blocks of fixed length. The length determines how much information can be contained in one block. If the length is \(r\text{,}\) there are \(2^r\) different values that a block can have. If the information being sent takes the form of text, each block might be a character. In that case, the length of a block may be seven, so that \(2^7 = 128\) block values can represent letters (both upper and lower case), digits, punctuation, and so on. During the transmission of data, noise can alter the signal so that what is received differs from what is sent. Figure \(\PageIndex{1}\) illustrates the problem that can be encountered if information is transmitted between two points.

Figure \(\PageIndex{1}\): A noisy transmission

Noise is a fact of life for anyone who tries to transmit information. Fortunately, in most situations, we could expect a high percentage of the pulses that are sent to be received properly. However, when large numbers of pulses are transmitted, there are usually some errors due to noise. For the remainder of the discussion, we will make assumptions about the nature of the noise and the message that we want to send. Henceforth, we will refer to the pulses as bits.

We will assume that our information is being sent along a binary symmetric channel. By this, we mean that any single bit that is transmitted will be received improperly with a certain fixed probability, \(p\text{,}\) independent of the bit value. The magnitude of \(p\) is usually quite small. To illustrate the process, we will assume that \(p = 0.001\text{,}\) which, in the real world, would be considered somewhat large. Since \(1 - p = 0.999\text{,}\) we can expect \(99.9\%\) of all bits to be properly received.

Suppose that our message consists of 3,000 bits of information, to be sent in blocks of three bits each. Two factors will be considered in evaluating a method of transmission. The first is the probability that the message is received with no errors. The second is the number of bits that will be transmitted in order to send the message. This quantity is called the rate of transmission:

\begin{equation*} \textrm{ Rate}= \frac{\textrm{ Message length}}{\textrm{ Number of bits transmitted}} \end{equation*}

As you might expect, as we devise methods to improve the probability of success, the rate will decrease.

Suppose that we ignore the noise and transmit the message without any coding. The probability of success is \(0.999^{3000}= 0.0497124\text{.}\) Therefore we only successfully receive the message in a totally correct form less than \(5\%\) of the time. The rate of \(\frac{3000}{3000} = 1\) certainly doesn't offset this poor probability.

Our strategy for improving our chances of success will be to send an encoded message across the binary symmetric channel. The encoding will be done in such a way that small errors can be identified and corrected. This idea is illustrated in Figure \(\PageIndex{2}\).

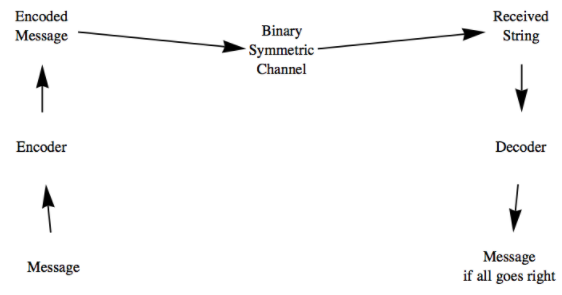Figure \(\PageIndex{2}\): The Coding Process

In our examples, the functions that will correspond to our encoding and decoding devices will all be homomorphisms between Cartesian products of \(\mathbb{Z}_2\text{.}\)

Error Detection

Suppose that each block of three bits \(a = \left(a_1, a_2 , a_3 \right)\) is encoded with the function \(e: \mathbb{Z}_2{}^3\to \mathbb{Z}_2{}^4\text{,}\) where

\begin{equation*} e(a) = \left(a _1, a _2 , a _3, a_1+_2a_2+_2a_3 \right) \end{equation*}

When the encoded block is received, the four bits will probably all be correct (they are correct approximately \(99.6\%\) of the time), but the added bit that is sent will make it possible to detect single errors in the block. Note that when \(e(a)\) is transmitted, the sum of its components is \(a_1+_2 a_2 +_2 a_3+_2 \left( a_1+_2 a_2+_2 a_3\right)= 0\text{,}\) since \(a_i+a_i=0\) in \(\mathbb{Z}_2\text{.}\)

If any single bit is garbled by noise, the sum of the received bits will be 1. The last bit of \(e(a)\) is called the parity bit. A parity error occurs if the sum of the received bits is 1. Since more than one error is unlikely when \(p\) is small, a high percentage of all errors can be detected.

At the receiving end, the decoding function acts on the four-bit block \(b = \left(b_1,b _2 ,b_3,b_4 \right)\) with the function \(d: \mathbb{Z}_2{}^4\to \mathbb{Z}_2^4\text{,}\) where

\begin{equation*} d(b) = \left(b_1,b _2 ,b_3,b_1+_2b _2 +_2b_3+_2b_4 \right) \end{equation*}

The fourth bit is called the parity-check bit. If no parity error occurs, the first three bits are recorded as part of the message. If a parity error occurs, we will assume that a retransmission of that block can be requested. This request can take the form of automatically having the parity-check bit of \(d(b)\) sent back to the source. If 1 is received, the previous block is retransmitted; if 0 is received, the next block is sent. This assumption of two-way communication is significant, but it is desirable to make this coding system useful. It is reasonable to expect that the probability of a transmission error in the opposite direction is also 0.001. Without going into the details, we will report that the probability of success is approximately 0.990 and the rate is approximately 3/5. The rate includes the transmission of the parity-check bit to the source.

Error Correction

Next, we will consider a coding process that can correct errors at the receiving end so that only one-way communication is needed. Before we begin, recall that every element of \(\mathbb{Z}_2{}^n\text{,}\) \(n \geq 1\text{,}\) is its own inverse; that is, \(-b = b\text{.}\) Therefore, \(a - b = a + b\text{.}\)

Noisy three-bit message blocks are difficult to transmit because they are so similar to one another. If \(a\) and \(b\) are in \(\mathbb{Z}_2{}^3\text{,}\) their difference, \(a +_2 b\text{,}\) can be thought of as a measure of how close they are. If \(a\) and \(b\) differ in only one bit position, one error can change one into the other. The encoding that we will introduce takes a block \(a = \left(a_1, a_2, a_3 \right)\) and produces a block of length 6 called the code word of \(a\text{.}\) The code words are selected so that they are farther from one another than the messages are. In fact, each code word will differ from each other code word by at least three bits. As a result, any single error will not push a code word close enough to another code word to cause confusion. Now for the details.

Let \(G=\left( \begin{array}{cccccc} 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ \end{array} \right)\text{.}\) We call \(G\) the generator matrix for the code, and let \(a = \left(a_1, a_2, a_3 \right)\) be our message.

Define \(e : \mathbb{Z}_2{}^3 \to \mathbb{Z}_2{}^6\) by

\begin{equation*} e(a) = a G = \left(a_1, a_2, a_3,a_4, a_5, a_6\right) \end{equation*}

where

\begin{equation*} \begin{array}{r@{}r@{}r@{}r@{}r@{}r@{}r@{}} a_4 &= & a_1 & {}+_2{} & a_2 & & \\ a_5 &= & a_1 & & &{}+_2{} & a_3 \\ a_6 &= & & & a_2 &{}+_2{} & a_3 \\ \end{array} \end{equation*}

Notice that \(e\) is a homomorphism. Also, if \(a\) and \(b\) are distinct elements of \(\mathbb{Z}_2{}^3\text{,}\) then \(c = a + b\) has at least one coordinate equal to 1. Now consider the difference between \(e(a)\) and \(e(b)\text{:}\)

\begin{equation*} \begin{split} e(a) + e(b) &= e(a + b) \\ & = e(c)\\ & = \left(d_1, d_2, d_3, d_4, d_5, d_6\right)\\ \end{split} \end{equation*}

Whether \(c\) has 1, 2, or 3 ones, \(e(c)\) must have at least three ones. This can be seen by considering the three cases separately. For example, if \(c\) has a single one, two of the parity bits are also 1. Therefore, \(e(a)\) and \(e(b)\) differ in at least three bits.

Now consider the problem of decoding the code words. Imagine that a code word, \(e(a)\text{,}\) is transmitted, and \(b= \left(b_1, b_2, b_3,b_4, b_5, b_6\right)\) is received. At the receiving end, we know the formula for \(e(a)\text{,}\) and if no error has occurred in transmission,

\begin{equation*} \begin{array}{c} b_1= a_1 \\ b_2=a_2 \\ b_3=a_3 \\ b_4=a_1+_2a_2 \\ b_5=a_1+_2a_3 \\ b_6=a_2+_2a_3 \\ \end{array} \Rightarrow \begin{array}{r@{}r@{}r@{}r@{}r@{}r@{}r@{}r@{}r@{}r@{}r@{}r@{}} b_1 & +_2 & b_2 & & &+_2& b_4& & & & &=0\\ b_1 & & & +_2 &b_3& & & +_2& b_5 & & &=0\\ & & b_2 & +_2 &b_3& & & & &+_2 &b_6&=0\\ \end{array} \end{equation*}

The three equations on the right are called parity-check equations. If any of them are not true, an error has occurred. This error checking can be described in matrix form.

Let

\begin{equation*} P=\left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \end{equation*}

\(P\) is called the parity-check matrix for this code. Now define \(p:\mathbb{Z}_2{}^6 \to \mathbb{Z}_2{}^3\) by \(p(b) = b P\text{.}\) We call \(p(b)\) the syndrome of the received block. For example, \(p(0,1,0,1,0,1)=(0,0,0)\) and \(p(1,1,1,1,0,0)=(1,0,0)\)

Note that \(p\) is also a homomorphism. If the syndrome of a block is \((0, 0, 0)\text{,}\) we can be almost certain that the message block is \(\left(b_1, b_2, b_3\right)\text{.}\)

Next we turn to the method of correcting errors. Despite the fact that there are only eight code words, one for each three-bit block value, the set of possible received blocks is \(\mathbb{Z}_2{}^6\text{,}\) with 64 elements. Suppose that \(b\) is not a code word, but that it differs from a code word by exactly one bit. In other words, it is the result of a single error in transmission. Suppose that \(w\) is the code word that \(b\) is closest to and that they differ in the first bit. Then \(b + w = (1, 0, 0, 0, 0, 0)\) and

\begin{equation*} \begin{split} p(b) & = p(b) + p(w)\quad \textrm{ since }p(w) = (0, 0, 0)\\ &=p(b+w)\quad\textrm{ since }p \textrm{ is a homomorphism}\\ & =p(1,0,0,0,0,0)\\ & =(1,1,0)\\ \end{split} \end{equation*}

Note that we haven't specified \(b\) or \(w\text{,}\) only that they differ in the first bit. Therefore, if \(b\) is received, there was probably an error in the first bit and \(p(b) = (1, 1, 0)\text{,}\) the transmitted code word was probably \(b + (1, 0, 0, 0, 0, 0)\) and the message block was \(\left(b_1+_2 1, b_2, b_3\right)\text{.}\) The same analysis can be done if \(b\) and \(w\) differ in any of the other five bits.

This process can be described in terms of cosets. Let \(W\) be the set of code words; that is, \(W = e\left(\mathbb{Z}_2{}^3 \right)\text{.}\) Since \(e\) is a homomorphism, \(W\) is a subgroup of \(\mathbb{Z}_2{}^6\text{.}\) Consider the factor group \(\left.\mathbb{Z}_2{}^6\right/W\text{:}\)

\begin{equation*} \lvert \mathbb{Z}_2{}^6/W \rvert =\frac{\lvert \mathbb{Z}_2{}^6 \rvert }{\lvert W \rvert}=\frac{64}{8}=8 \end{equation*}

Suppose that \(b_1\) and \(b_2\) are representatives of the same coset. Then \(b_1= b_2+w\) for some \(w\) in \(W\text{.}\) Therefore,

\begin{equation*} \begin{split} p\left(b _1\right) &= p\left(b_1\right) + p(w)\quad \textrm{ since } p(w) = (0, 0, 0)\\ &= p\left(b_1 + w\right)\\ &= p\left(b_2 \right)\\ \end{split} \end{equation*}

and so \(b_1\) and \(b_2\) have the same syndrome.

Finally, suppose that \(d_1\) and \(d_2\) are distinct and both have only a single coordinate equal to 1. Then \(d_1+d_2\) has exactly two ones. Note that the identity of \(\mathbb{Z}_2{}^6\text{,}\) \((0, 0, 0, 0, 0, 0)\text{,}\) must be in \(W\text{.}\) Since \(d_1+d_2\) differs from the identity by two bits, \(d_1+d_2 \notin W\text{.}\) Hence \(d_1\) and \(d_2\) belong to distinct cosets. The reasoning above serves as a proof of the following theorem.

Theorem \(\PageIndex{1}\)

There is a system of distinguished representatives of \(\left.\mathbb{Z}_2{}^6\right/W\) such that each of the six-bit blocks having a single 1 is a distinguished representative of its own coset.

Now we can describe the error-correcting process. First match each of the blocks with a single 1 with its syndrome. In addition, match the identity of \(W\) with the syndrome \((0, 0, 0)\) as in the table below. Since there are eight cosets of \(W\text{,}\) select any representative of the eighth coset to be distinguished. This is the coset with syndrome \((1, 1, 1)\text{.}\)

\begin{equation*} \begin{array}{c|c} \begin{array}{c} \textrm{ Syndrome} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array} \\ \end{array} & \begin{array}{c} \textrm{ Error} \textrm{ Correction} \\ \hline \begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \\ \end{array} \\ \end{array} \end{equation*}

When block \(b\) is received, you need only compute the syndrome, \(p(b)\text{,}\) and add to \(b\) the error correction that matches \(p(b)\text{.}\)

We will conclude this example by computing the probability of success for our hypothetical situation. It is \(\left(0.999^6 + 6 \cdot 0.999^5 \cdot 0.001\right)^{1000}=0.985151\text{.}\) The rate for this code is \(\frac{1}{2}\text{.}\)

Example \(\PageIndex{1}\): Another Linear Code

Consider the linear code with generator matrix

\begin{equation*} G = \left( \begin{array}{ccccc} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 \\ \end{array} \right). \end{equation*}

Since \(G\) is \(3 \times 5\text{,}\) this code encodes three bits into five bits. The natural question to ask is what detection or correction does it afford? We can answer this question by constructing the parity check matrix. We observe that if \(\vec{b}=(b_1, b_2, b_3)\) the encoding function is

\begin{equation*} e(\vec{b}) = \vec{b}G = (b_1,b_1+b_2,b_2,b_1+b_3,b_3) \end{equation*}

where addition is mod 2 addition. If we receive five bits \((c_1,c_2,c_3,c_4,c_5)\) and no error has occurred, the following two equations would be true.

\[\begin{align}c_1+c_2+c_3&=0\label{eq:1} \\ c_1+c_4+c_5&=0\label{eq:2}\end{align}\]

Notice that in general, the number of parity check equations is equal to the number of extra bits that are added by the encoding function. These equations are equivalent to the single matrix equation \((c_1,c_2,c_3,c_4,c_5)H = \vec{0}\text{,}\) where

\begin{equation*} H = \left(\begin{array}{cc} 1 & 1 \\ 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ \end{array} \right) \end{equation*}

At a glance, we can see that this code will not correct most single bit errors. Suppose an error \(\vec{e}=(e_1,e_2,e_3,e_4,e_5)\) is added in the transmission of the five bits. Specifically, suppose that 1 is added (mod 2) in position \(j\text{,}\) where \(1 \leq j\leq 5\) and the other coordinates of \(\vec{e}\) are 0. Then when we compute the syndrome of our received transmission, we see that

\begin{equation*} \vec{c}H = (\vec{b}G + \vec{e})H = (\vec{b}G)H + \vec{e}H = \vec{e}H. \end{equation*}

But \(\vec{e}H\) is the \(j^{th}\) row of \(H\text{.}\) If the syndrome is \((1,1)\) we know that the error occurred in position 1 and we can correct it. However, if the error is in any other position we can't pinpoint its location. If the syndrome is \((1,0)\text{,}\) then the error could have occurred in either position 2 or position 3. This code does detect all single bit errors but only corrects one fifth of them.

Exercises

Exercise \(\PageIndex{1}\)

If the error-detecting code is being used, how would you act on the following received blocks?

1. \(\displaystyle (1, 0, 1, 1)\)
2. \(\displaystyle (1, 1, 1, 1)\)
3. \(\displaystyle (0, 0, 0, 0)\)

Answer

1. Error detected, since an odd number of 1's was received; ask for retransmission.
2. No error detected; accept this block.
3. No error detected; accept this block.

Exercise \(\PageIndex{2}\)

Express the encoding and decoding functions for the error-detecting code using matrices.

Exercise \(\PageIndex{3}\)

If the error-correcting code from this section is being used, how would you decode the following blocks? Expect an error that cannot be fixed with one of these.

1. \(\displaystyle (1,0,0,0,1,1)\)
2. \(\displaystyle (1,0,1,0,1,1)\)
3. \(\displaystyle (0,1,1,1,1,0)\)
4. \(\displaystyle (0,0,0,1,1,0)\)
5. \(\displaystyle (1,0,0,0,0,1)\)
6. \(\displaystyle (1,0,0,1,0,0)\)

Answer

1. Syndrome = \((1,0,1)\text{.}\) Corrected coded message is \((1,1,0,0,1,1)\) and original message was \((1, 1, 0)\text{.}\)
2. Syndrome = \((1,1,0)\text{.}\) Corrected coded message is \((0,0,1,0,1,1)\) and original message was \((0, 0, 1)\text{.}\)
3. Syndrome = \((0,0,0)\text{.}\) No error, coded message is \((0,1,1,1,1,0)\) and original message was \((0, 1, 1)\text{.}\)
4. Syndrome = \((1, 1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)
5. Syndrome = \((1,1,1)\text{.}\) This syndrome occurs only if two bits have been switched. No reliable correction is possible.
6. Syndrome = \((0,1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)

Exercise \(\PageIndex{5}\)

Consider the linear code defined by the generator matrix

\begin{equation*} G=\left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ \end{array} \right) \end{equation*}

1. What size blocks does this code encode and what is the length of the code words?
2. What are the code words for this code?
3. With this code, can you detect single bit errors? Can you correct all, some, or no single bit errors?

Answer

Let \(G\) be the \(9 \times 10\) matrix obtained by augmenting the \(9\times 9\) . The function \(e:\mathbb{Z}_2{}^9\to \mathbb{Z}_2{}^{10}\) defined by \(e(a) = a G\) will allow us to detect single errors, since \(e(a)\) will always have an even number of ones.

Exercise \(\PageIndex{6}\): Rectangular Codes

To build a rectangular code, you partition your message into blocks of length \(m\) and then factor \(m\) into \(k_1\cdot k_2\) and arrange the bits in a \(k_1 \times k_2\) rectangular array as in the figure below. Then you add parity bits along the right side and bottom of the rows and columns. The code word is then read row by row.

\begin{equation*} \begin{array}{cccccc} \blacksquare & \blacksquare & \blacksquare & \cdots & \blacksquare & \square \\ \blacksquare & \blacksquare & \blacksquare & \cdots & \blacksquare & \square \\ \vdots & \vdots & \vdots & & \vdots & \vdots \\ \blacksquare & \blacksquare & \blacksquare & \cdots & \blacksquare & \square \\ \square & \square & \square & \cdots & \square & \\ \end{array} \quad \begin{array}{c} \textrm{ }\blacksquare = \textrm{ message} \textrm{ bit} \\ \square =\textrm{ parity} \textrm{ bit} \\ \end{array} \end{equation*}

For example, if \(m\) is 4, then our only choice is a 2 by 2 array. The message 1101 would be encoded as

\begin{equation*} \begin{array}{cc|c} 1 & 1 & 0\\ 0 & 1 & 1\\ \hline 1 & 0 &\\ \end{array} \end{equation*}

and the code word is the string 11001110.

1. Suppose that you were sent four bit messages using this code and you received the following strings. What were the messages, assuming no more than one error in the transmission of coded data?
   1. 11011000
   2. 01110010
   3. 10001111
2. If you encoded \(n^2\) bits in this manner, what would be the rate of the code?
3. Rectangular codes are linear codes. For the 3 by 2 rectangular code, what are the generator and parity check matrices?

Exercise \(\PageIndex{7}\)

Suppose that the code in Example \(\PageIndex{1}\) is expanded to add the column

\begin{equation*} \left(\begin{array}{c} 0 \\ 1 \\ 1 \\ \end{array} \right) \end{equation*}

to the generator matrix \(G\text{,}\) can all single bit errors be corrected? Explain your answer.

Answer

Yes, you can correct all single bit errors because the parity check matrix for the expanded code is

\begin{equation*}
H = \left(\begin{array}{ccc} 
1 & 1 & 0\\
1 & 0 & 0\\
1 & 0 & 1\\
0 & 1 & 0\\
0 & 1 & 1\\
0 & 0 & 1\\
\end{array} \right).
\end{equation*}

Since each possible syndrome of single bit errors is unique we can correct any error.