10.2: Proporciones

Last updated
Save as PDF

Page ID: 127652

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

ser capaz de describir proporciones y encontrar el factor faltante en una proporción
ser capaz de trabajar con proporciones que involucren tasas

Ratios, Tasas y Proporciones

Definición: Ratio, Tasa

Hemos definido una relación como una comparación, por división, de dos números puros o dos números denominados similares. Hemos definido una tasa como una comparación, por división, de dos números denominados diferentes.

Definición: Proporción

Una proporción es una afirmación de que dos ratios o tasas son iguales. Los siguientes dos ejemplos muestran cómo leer proporciones.

$Tres cuartos equivale a seis octavos. 3 es a cuatro como seis es a ocho. 25 millas divididas por 1 galón equivale a 50 millas divididas por 2 galones. 25 millas es a 1 galón ya que 50 millas es a 2 galones.$

Conjunto de Muestras A

Escribe o lee cada proporción.

$\dfrac{3}{5} = \dfrac{12}{20}$

Solución

3 es a 5 como 12 es a 20

Conjunto de Muestras A

$\dfrac{\text{10 items}}{\text{5 dollars}} = \dfrac{\text{2 items}}{\text{1 dollar}}$

Solución

10 artículos es a 5 dólares ya que 2 artículos es a 1 dólar

Conjunto de Muestras A

8 es a 12 como 16 es a 24.

Solución

$\dfrac{8}{12} = \dfrac{16}{24}$

Conjunto de Muestras A

50 miligramos de vitamina C es a 1 tableta ya que 300 miligramos de vitamina C es a 6 tabletas.

Solución

$\dfrac{50}{1} = \dfrac{300}{6}$

Conjunto de práctica A

Escribe o lee cada proporción.

$\dfrac{3}{8} = \dfrac{6}{16}$

Contestar: 3 es a 8 como 6 es a 16

Conjunto de práctica A

$\dfrac{\text{2 people}}{\text{1 window}} = \dfrac{\text{10 people}}{\text{5 windows}}$

Contestar: 2 personas son a 1 ventana ya que 10 personas son a 5 ventanas

Conjunto de práctica A

15 es a 4 como 75 es a 20.

Contestar: $\dfrac{15}{4} = \dfrac{75}{20}$

Conjunto de práctica A

2 platos son a 1 bandeja ya que 20 platos son a 10 charolas.

Contestar: \ (\ dfrac {\ texto {2 platos}} {\ texto {1 bandeja}} =\ dfrac {\ texto {20 platos}} {\ texto {10 bandejas}}

Encontrar el factor faltante en una proporción

Muchos problemas prácticos pueden resolverse escribiendo la información dada como proporciones. Dichas proporciones estarán compuestas por tres números especificados y un número desconocido. Es costumbre dejar que una letra, como$x$, represente el número desconocido. Un ejemplo de tal proporción es

$\dfrac{x}{4} = \dfrac{20}{16}$

Esta proporción se lee como "$x$es a 4 como 20 es a 16”.

Existe un método para resolver estas proporciones que se basa en la igualdad de fracciones. Recordemos que dos fracciones son equivalentes si y sólo si sus productos cruzados son iguales. Por ejemplo,

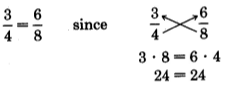
$Tres cuartas partes equivalen a seis octavos. Junto a esta ecuación están las mismas dos fracciones, con flechas apuntando desde los denominadores al numerador de la fracción opuesta, indicando un producto cruzado. El producto cruzado es 3 por 8 es igual a 6 veces 4, o 24 es igual a 24.$

Observe que en una proporción que contenga tres números especificados y una letra que represente una cantidad desconocida, que independientemente de donde aparezca la letra, siempre ocurre la siguiente situación.

$\underbrace{(\text{number}) \cdot (\text{letter}) = (\text{number}) \cdot (\text{number})}_{}$

Esto lo reconocemos como una declaración de multiplicación. En concreto, se trata de una declaración de factor faltante. (Véase [link] para una discusión de declaraciones de multiplicación.) Por ejemplo,

$\begin{array} {ll} {\dfrac{x}{4} = \dfrac{20}{16}} & {\text{ means that } 16 \cdot x = 4 \cdot 20} \\ {\dfrac{4}{x} = \dfrac{16}{20}} & {\text{ means that } 4 \cdot 20 = 16 \cdot x} \\ {\dfrac{5}{4} = \dfrac{x}{16}} & {\text{ means that } 5 \cdot 16 = 4 \cdot x} \\ {\dfrac{5}{4} = \dfrac{20}{x}} & {\text{ means that } 5 \cdot x = 4 \cdot 20} \end{array}$

Cada una de estas declaraciones es una declaración de multiplicación. Específicamente, cada uno es una declaración de factor faltante. (La letra utilizada aquí es$x$, mientras que$M$ se utilizó en [link].)

Encontrar el factor faltante en una proporción
El factor faltante en una declaración de factor faltante se puede determinar dividiendo el producto por el factor conocido, es decir, si$x$ representa el factor faltante, entonces

$x = \text{(product)} \div \text{(known factor)}$

Conjunto de Muestras B

Encuentra el número desconocido en cada proporción.

$\dfrac{x}{4} = \dfrac{20}{16}$. Encuentra el producto cruzado.

Solución

$\begin{array} {ccll} {16 \cdot x} & = & {20 \cdot 4} & {} \\ {16 \cdot x} & = & {80} & {\text{ Divide the product 80 by the known factor 16.}} \\ {x} & = & {\dfrac{80}{16}} & {} \\ {x} & = & {5} & {\text{ The unkown number is 5.}} \end{array}$

Esto significa que$\dfrac{5}{4} = \dfrac{20}{16}$, o 5 es a 4 como 20 es a 16.

Conjunto de Muestras B

$\dfrac{5}{x} = \dfrac{20}{16}$. Encuentra el producto cruzado.

Solución

$\begin{array} {ccll} {5 \cdot 16} & = & {20 \cdot x} & {} \\ {80} & = & {20 \cdot x} & {\text{ Divide the product 80 by the known factor 20.}} \\ {\dfrac{80}{20}} & = & {x} & {} \\ {4} & = & {x} & {\text{ The unkown number is 4.}} \end{array}$

Esto significa que$\dfrac{5}{4} = \dfrac{20}{16}$, o 5 es a 4 como 20 es a 16.

Conjunto de Muestras B

$\dfrac{16}{3} = \dfrac{64}{x}$. Encuentra el producto cruzado.

Solución

$\begin{array} {ccll} {16 \cdot x} & = & {64 \cdot 3} & {} \\ {16 \cdot x} & = & {192} & {\text{ Divide 192 by 16.}} \\ {x} & = & {\dfrac{192}{16}} & {} \\ {x} & = & {12} & {\text{ The unkown number is 12.}} \end{array}$

Esto significa que$\dfrac{16}{3} = \dfrac{64}{12}$, o 16 es a 3 como 64 es a 12.

Conjunto de Muestras B

$\dfrac{9}{8} = \dfrac{x}{40}$. Encuentra el producto cruzado.

Solución

$\begin{array} {ccll} {9 \cdot 40} & = & {8 \cdot x} & {} \\ {360} & = & {8 \cdot x} & {\text{ Divide 360 by 8.}} \\ {\dfrac{360}{8}} & = & {x} & {} \\ {45} & = & {x} & {\text{ The unkown number is 45.}} \end{array}$

Set de práctica B

Encuentra el número desconocido en cada proporción.

$\dfrac{x}{8} = \dfrac{12}{32}$

Contestar: $x = 3$

Set de práctica B

$\dfrac{7}{x} = \dfrac{14}{10}$

Contestar: $x = 5$

Set de práctica B

$\dfrac{9}{11} = \dfrac{x}{55}$

Contestar: $x = 45$

Set de práctica B

$\dfrac{1}{6} = \dfrac{8}{x}$

Contestar: $x = 48$

Proporciones que implican tasas

Recordemos que una tasa es una comparación, por división, de números denominados distintos. Debemos tener cuidado a la hora de establecer proporciones que involucren tarifas. La forma es importante. Por ejemplo, si una tarifa involucra dos tipos de unidades, digamos unidad tipo 1 y unidad tipo 2, podemos escribir

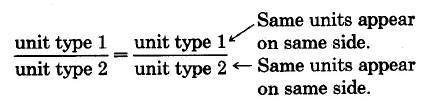
$unidad tipo 1 sobre unidad tipo 2 equivale a unidad tipo 1 sobre unidad tipo 2. Las mismas unidades aparecen del mismo lado, en este caso, las mismas unidades forman parte de la misma fracción.$

$unidad tipo 1 sobre unidad tipo 2 equivale a unidad tipo 1 sobre unidad tipo 2. Las mismas unidades aparecen del mismo lado, en este caso, la misma unidad está en ambos denominadores y la misma unidad está en ambos numeradores.$

Ambos productos cruzados producen una declaración del tipo

$(\text{unit type 1}) \cdot (\text{unit type 2}) = (\text{unit type 1}) \cdot (\text{unit type 2})$

lo que tomamos para significar la comparación

$Una comparación de tipos de unidades.$

Ejemplos de proporciones expresadas correctamente son los siguientes:

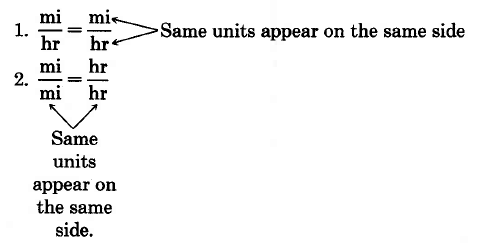
$Dos proporciones. El primero es millas sobre hr equivale a millas sobre hora, donde la misma unidad siempre está en el denominador. El segundo es millas sobre millas equivale a horas sobre horas, donde la misma unidad está en su propia fracción.$

Sin embargo, si escribimos el mismo tipo de unidades en diferentes lados, como,

$\dfrac{\text{unit type 1}}{\text{unit type 2}} = \dfrac{\text{unit type 2}}{\text{unit type 1}}$

el producto cruzado produce una declaración de la forma

$Un gráfico que muestra la comparación de diferentes tipos de unidades.$

Podemos ver que esta es una comparación incorrecta al observar el siguiente ejemplo: Es incorrecto escribir

$\dfrac{\text{2 hooks}}{\text{3 poles}} = \dfrac{\text{6 poles}}{\text{4 hooks}}$

por dos razones.

El producto cruzado es numéricamente incorrecto:$(2 \cdot 4 \ne 3 \cdot 6)$
El producto cruzado produce la declaración “los ganchos son a los ganchos como los postes lo son a los postes”, lo cual no tiene sentido.

Ejercicios

Ejercicio$\PageIndex{1}$

Una declaración de que dos proporciones o son iguales se llama a.

Contestar: tasas, proporción

Para los siguientes 9 problemas, escriba cada proporción en forma fraccionaria.

Ejercicio$\PageIndex{2}$

3 es a 7 como 18 es a 42.

Ejercicio$\PageIndex{3}$

1 es a 11 como 3 es a 33.

Contestar: $\dfrac{1}{11} = \dfrac{3}{33}$

Ejercicio$\PageIndex{4}$

9 es a 14 como 27 es a 42.

Ejercicio$\PageIndex{5}$

6 es a 90 como 3 es a 45.

Contestar: $\dfrac{6}{90} = \dfrac{3}{45}$

Ejercicio$\PageIndex{6}$

5 litros es a 1 botella ya que 20 litros es a 4 botellas.

Ejercicio$\PageIndex{7}$

18 gramos de cobalto es a 10 gramos de plata ya que 36 gramos de cobalto es a 20 gramos de plata.

Contestar: $\dfrac{\text{18 gr cobalt}}{\text{10 gr silver}} = \dfrac{\text{36 gr cobalt}}{\text{20 gr silver}}$

Ejercicio$\PageIndex{8}$

4 tazas de agua es a 1 taza de azúcar ya que 32 tazas de agua es a 8 tazas de azúcar.

Ejercicio$\PageIndex{9}$

3 personas ausentes es a 31 personas presentes como 15 personas ausentes es a 155 personas presentes.

Contestar: $\dfrac{\text{3 people absent}}{\text{31 people present}} = \dfrac{\text{15 people absent}}{\text{155 people present}}$

Ejercicio$\PageIndex{10}$

6 dólares es a 1 hora ya que 90 dólares es a 15 horas.

Para los siguientes 10 problemas, escribe cada proporción como una oración.

Ejercicio$\PageIndex{11}$

$\dfrac{3}{4} = \dfrac{15}{20}$

Contestar: 3 es a 4 como 15 es a 20

Ejercicio$\PageIndex{12}$

$\dfrac{1}{8} = \dfrac{5}{40}$

Ejercicio$\PageIndex{13}$

$\dfrac{\text{3 joggers}}{\text{100 feet}} = \dfrac{\text{6 joggers}}{\text{200 feet}}$

Contestar: 3 joggers son a 100 pies ya que 6 joggers son a 200 pies

Ejercicio$\PageIndex{14}$

$\dfrac{\text{12 marshmallows}}{\text{3 sticks}} = \dfrac{\text{36 marshmallows}}{\text{9 sticks}}$

Ejercicio$\PageIndex{15}$

$\dfrac{\text{40 miles}}{\text{80 miles}} = \dfrac{\text{2 gallons}}{\text{4 gallons}}$

Contestar: 40 millas son a 80 millas ya que 2 galones son a 4 galones

Ejercicio$\PageIndex{16}$

$\dfrac{\text{4 couches}}{\text{10 couches}} = \dfrac{\text{2 houses}}{\text{5 houses}}$

Ejercicio$\PageIndex{17}$

$\dfrac{\text{1 person}}{\text{1 job}} = \dfrac{\text{8 people}}{\text{8 jobs}}$

Contestar: 1 persona es a 1 empleo ya que 8 personas son a 8 empleos

Ejercicio$\PageIndex{18}$

$\dfrac{\text{1 popsicle}}{\text{2 children}} = \dfrac{\dfrac{1}{2} \text{8 popsicle}}{\text{1 child}}$

Ejercicio$\PageIndex{19}$

$\dfrac{\text{2,000 pounds}}{\text{1 ton}} = \dfrac{\text{60,000 pounds}}{\text{30 tons}}$

Contestar: 2,000 libras son a 1 tonelada ya que 60,000 libras son a 30 toneladas

Ejercicio$\PageIndex{20}$

$\dfrac{\text{1 table}}{\text{5 tables}} = \dfrac{\text{2 people}}{\text{10 people}}$

Para los siguientes 10 problemas, resolver cada proporción.

Ejercicio$\PageIndex{21}$

$\dfrac{x}{5} = \dfrac{6}{15}$

Contestar: $x = 2$

Ejercicio$\PageIndex{22}$

$\dfrac{x}{10} = \dfrac{28}{40}$

Ejercicio$\PageIndex{23}$

$\dfrac{5}{x} = \dfrac{10}{16}$

Contestar: $x = 8$

Ejercicio$\PageIndex{24}$

$\dfrac{13}{x} = \dfrac{39}{60}$

Ejercicio$\PageIndex{25}$

$\dfrac{1}{3} = \dfrac{x}{24}$

Contestar: $x = 8$

Ejercicio$\PageIndex{26}$

$\dfrac{7}{12} = \dfrac{x}{60}$

Ejercicio$\PageIndex{27}$

$\dfrac{8}{3} = \dfrac{72}{x}$

Contestar: $x = 27$

Ejercicio$\PageIndex{28}$

$\dfrac{16}{1} = \dfrac{48}{x}$

Ejercicio$\PageIndex{29}$

$\dfrac{x}{25} = \dfrac{200}{125}$

Contestar: $x = 40$

Ejercicio$\PageIndex{30}$

$\dfrac{65}{30} = \dfrac{x}{60}$

Para los siguientes 5 problemas, expresar cada oración como una proporción y luego resolver la proporción.

Ejercicio$\PageIndex{31}$

5 sombreros son a 4 abrigos ya que los$x$ sombreros son a 24 abrigos.

Contestar: $x = 30$

Ejercicio$\PageIndex{32}$

$x$los cojines son para 2 sofás ya que 24 cojines son para 16 sofás.

Ejercicio$\PageIndex{33}$

1 nave espacial es a 7 astronautas ya que 5 naves espaciales son para$x$ astronautas.

Contestar: $x = 35$

Ejercicio$\PageIndex{34}$

56 microchips son para placas de$x$ circuito ya que 168 microchips son a 3 placas de circuito.

Ejercicio$\PageIndex{35}$

18 calculadoras son a 90 calculadoras ya que$x$ los estudiantes son a 150 estudiantes.

Contestar: $x = 30$

Ejercicio$\PageIndex{36}$

$x$dólares son a $40.000 ya que 2 sacos son a 1 saco.

Indicar si la proporción es verdadera o falsa.

Ejercicio$\PageIndex{37}$

$\dfrac{3}{16} = \dfrac{12}{64}$

Contestar: true

Ejercicio$\PageIndex{38}$

$\dfrac{2}{15} = \dfrac{10}{75}$

Ejercicio$\PageIndex{39}$

$\dfrac{1}{9} = \dfrac{3}{30}$

Contestar: false

Ejercicio$\PageIndex{40}$

$\dfrac{\text{6 knives}}{\text{7 forks}} = \dfrac{\text{12 knives}}{\text{15 forks}}$

Ejercicio$\PageIndex{41}$

$\dfrac{\text{33 miles}}{\text{1 gallon}} = \dfrac{\text{99 miles}}{\text{3 gallons}}$

Contestar: true

Ejercicio$\PageIndex{42}$

$\dfrac{\text{320 feet}}{\text{5 seconds}} = \dfrac{\text{65 feet}}{\text{1 second}}$

Ejercicio$\PageIndex{43}$

$\dfrac{\text{35 students}}{\text{70 students}} = \dfrac{\text{1 class}}{\text{2 classes}}$

Contestar: true

Ejercicio$\PageIndex{44}$

$\dfrac{\text{9 ml chloride}}{\text{45 ml chloride}} = \dfrac{\text{1 test tube}}{\text{7 test tubes}}$

Ejercicios para la revisión

Ejercicio$\PageIndex{43}$

([link]) Usa los números 5 y 7 para ilustrar la propiedad conmutativa de la suma.

Contestar: $5 + 7 = 12$
$7 + 5 = 12$

Ejercicio$\PageIndex{44}$

([link]) Usa los números 5 y 7 para ilustrar la propiedad conmutativa de la multiplicación.

Ejercicio$\PageIndex{43}$

([link]) Encuentra la diferencia. $\dfrac{5}{14} - \dfrac{3}{22}$.

Contestar: $\dfrac{17}{77}$

Ejercicio$\PageIndex{44}$

([link]) Encuentra el producto. $8.06129 \cdot 1,000$.

Ejercicio$\PageIndex{43}$

([link]) Escribe la forma fraccionaria simplificada de la tasa “dieciséis frases a dos párrafos”.

Contestar: $\dfrac{\text{8 sentences}}{\text{1 paragraph}}$

Search

Text Color

Text Size

Margin Size

Font Type