12.2: Perímetro, Circunferencia y Área
- Page ID
- 127667
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.2.1: Cuadriláteros
- Identificar propiedades, incluyendo mediciones de ángulo, de cuadriláteros.
Introducción
Los cuadriláteros son un tipo especial de polígono. Al igual que con los triángulos y otros polígonos, los cuadriláteros tienen propiedades especiales y pueden clasificarse por características de sus ángulos y lados. Comprender las propiedades de diferentes cuadriláteros puede ayudarte a resolver problemas que involucran este tipo de polígono.
Definición de un cuadrilátero
Escogiendo el nombre “cuadrilátero” te ayuda a entender a qué se refiere. El prefijo “quad-” significa “cuatro”, y “lateral” se deriva de la palabra latina para “lado”. Entonces un cuadrilátero es un polígono de cuatro lados.
Al tratarse de un polígono, ya sabes que se trata de una figura bidimensional conformada por lados rectos. Un cuadrilátero también tiene cuatro ángulos formados por sus cuatro lados. A continuación se presentan algunos ejemplos de cuadriláteros. Observe que cada figura tiene cuatro lados rectos y cuatro ángulos.
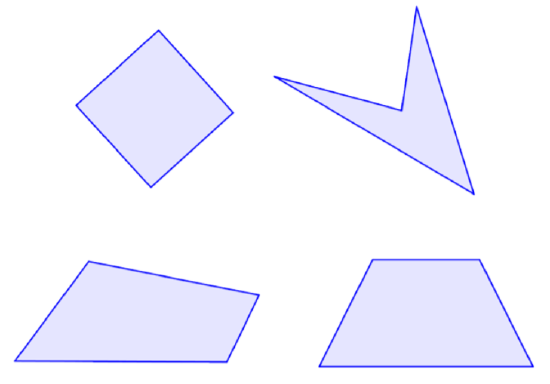
Ángulos interiores de un cuadrilátero
La suma de los ángulos interiores de cualquier cuadrilátero es de 360°. Considera los dos ejemplos a continuación.
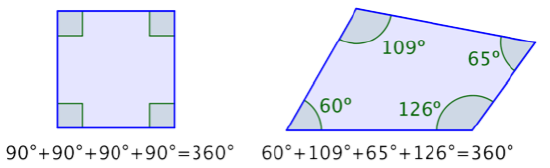
Podrías dibujar muchos cuadriláteros como estos y medir cuidadosamente los cuatro ángulos. Encontrarías que por cada cuadrilátero, la suma de los ángulos interiores siempre será de 360°.
También puedes usar tus conocimientos de triángulos como una forma de entender por qué la suma de los ángulos interiores de cualquier cuadrilátero es de 360°. Cualquier cuadrilátero se puede dividir en dos triángulos como se muestra en las imágenes a continuación.
En la primera imagen, los cuadriláteros se han dividido cada uno en dos triángulos. Se muestran las medidas de ángulo de un triángulo para cada uno.
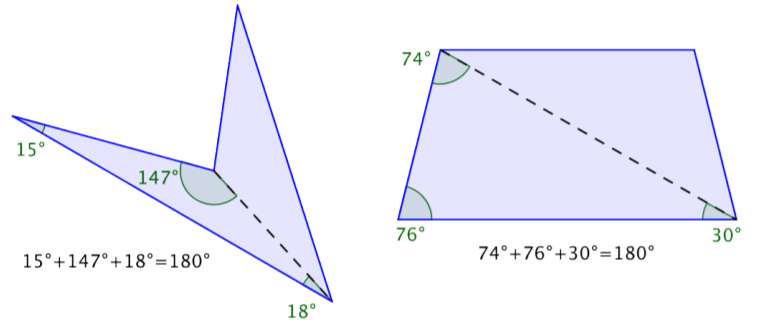
Estas medidas suman 180º. Ahora mira las medidas para los otros triángulos, ¡también suman 180º!
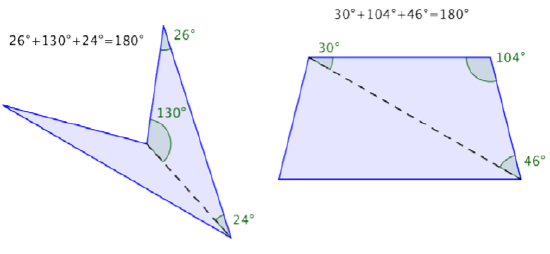
Dado que la suma de los ángulos interiores de cualquier triángulo es de 180° y hay dos triángulos en un cuadrilátero, la suma de los ángulos para cada cuadrilátero es de 360°.
Tipos Específicos de Cuadriláteros
Empecemos por examinar el grupo de cuadriláteros que tienen dos pares de lados paralelos. Estos cuadriláteros se llaman paralelogramos. Toman una variedad de formas, pero a continuación se muestra un ejemplo clásico.
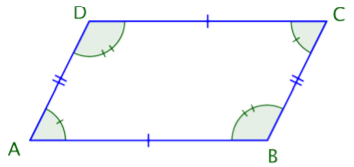
Imagina extender los pares de lados opuestos. Nunca se cruzarían porque son paralelos. Observe, también, que los ángulos opuestos de un paralelogramo son congruentes, al igual que los lados opuestos. (Recuerda que “congruente” significa “del mismo tamaño”.) El símbolo geométrico para congruente es\(≅\), por lo que puedes escribir A C y B D Los lados paralelos también tienen la misma longitud:\(\overline{AB} ≅ \overline{DC}\) y\(\overline{BC} ≅ \overline{AD}\). Estas relaciones son ciertas para todos los paralelogramos.
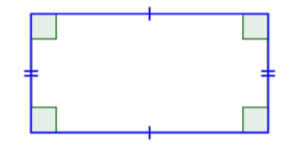
Hay dos casos especiales de paralelogramos que te serán familiares desde tus primeras experiencias con formas geométricas. El primer caso especial se llama rectángulo. Por definición, un rectángulo es un paralelogramo porque sus pares de lados opuestos son paralelos. Un rectángulo también tiene la característica especial de que todos sus ángulos son ángulos rectos; sus cuatro ángulos son congruentes.
El otro caso especial de un paralelogramo es un tipo especial de rectángulo, un cuadrado. Un cuadrado es una de las formas geométricas más básicas. Se trata de un caso especial de un paralelogramo que tiene cuatro lados congruentes y cuatro ángulos rectos.
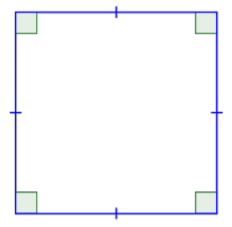
Un cuadrado también es un rectángulo porque tiene dos juegos de lados paralelos y cuatro ángulos rectos. Un cuadrado es también un paralelogramo porque sus lados opuestos son paralelos. Entonces, un cuadrado se puede clasificar en cualquiera de estas tres formas, siendo “paralelogramo” la descripción menos específica y “cuadrado”, la más descriptiva.
Otro cuadrilátero que podrías ver se llama rombo. Los cuatro lados de un rombo son congruentes. Sus propiedades incluyen que cada par de lados opuestos es paralelo, convirtiéndolo también en un paralelogramo.
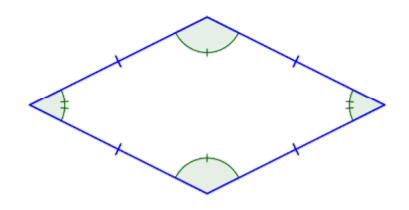
En resumen, todos los cuadrados son rectángulos, pero no todos los rectángulos son cuadrados. Todos los rectángulos son paralelogramos, pero no todos los paralelogramos son rectángulos. Y todas estas formas son cuadriláteros.
El siguiente diagrama ilustra la relación entre los diferentes tipos de cuadriláteros.
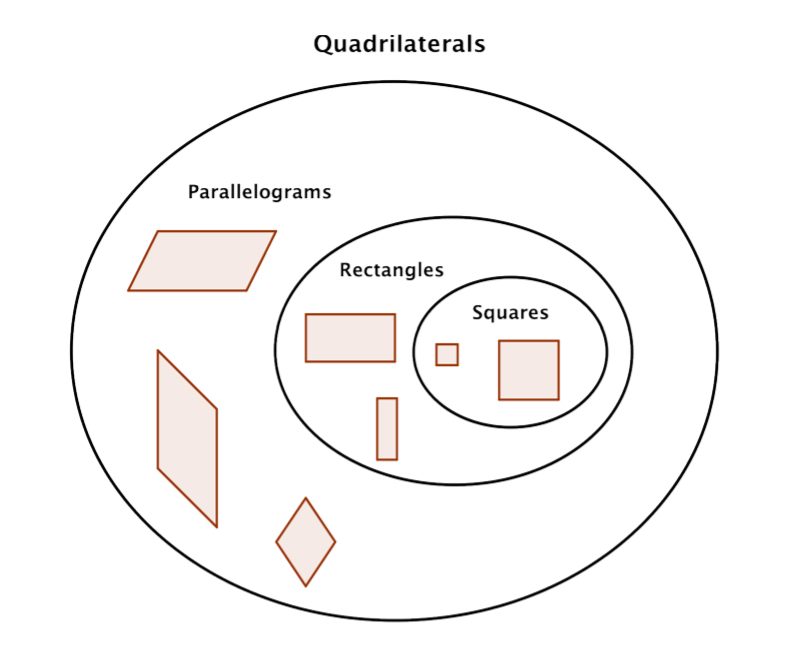
Se pueden utilizar las propiedades de los paralelogramos para resolver problemas. Considera el ejemplo que sigue.
Determinar las medidas de M y L.
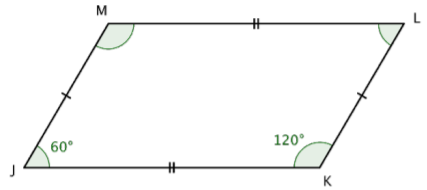
Solución
Identificar ángulos opuestos.
L es opuesto J
M es opuesto K
Una propiedad de los paralelogramos es que los ángulos opuestos son congruentes.
L J
M K
Utilice las medidas de ángulo dadas para determinar medidas de ángulos opuestos.
mj = 60°, entonces mL = 60°
Mk = 120°, entonces Mm = 120°
Respuesta: ml = 60° y mm = 120°
Trapecios
Hay otro tipo especial de cuadrilátero. Este cuadrilátero tiene la propiedad de tener sólo un par de lados opuestos que son paralelos. Aquí hay un ejemplo de trapecio.
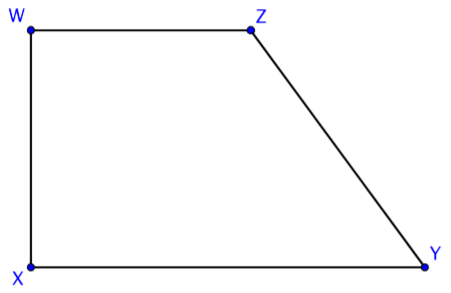
Observe eso\(\overline{XY} || \overline{WZ}\), y eso\(\overline{WX}\) y no\(\overline{ZY}\) son paralelos. Se puede imaginar fácilmente que si extendieras los lados\(\overline{WX}\) y\(\overline{ZY}\), ellos se cruzarían por encima de la figura.
Si los lados no paralelos de un trapecio son congruentes, el trapecio se llama trapecio isósceles. Al igual que el triángulo de nombre similar que tiene dos lados de igual longitud, el trapecio isósceles tiene un par de lados opuestos de igual longitud. El otro par de lados opuestos es paralelo. A continuación se muestra un ejemplo de un trapecio isósceles.
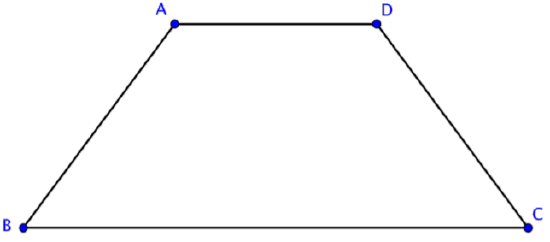
En este trapecio ABCD,\(\overline{BC} || \overline{AD}\) y\(\overline{AB} ≅ \overline{CD}\).
¿Cuál de las siguientes afirmaciones es cierta?
A) Algunos trapecios son paralelogramos.
B) Todos los trapecios son cuadriláteros.
C) Todos los rectángulos son cuadrados.
D) Una forma no puede ser un paralelogramo y un cuadrilátero.
Se pueden utilizar las propiedades de los cuadriláteros para resolver problemas que involucran trapecios. Considera el siguiente ejemplo.
Encuentra la medida de Q.
Solución
La suma de las medidas de los ángulos interiores de un cuadrilátero es de 360°.
mp + mq + mr + ms = 360°
El símbolo cuadrado indica un ángulo recto.
Mr = 90°
Ms = 90°
Dado que se dan tres de las cuatro medidas de ángulo, puede encontrar la cuarta medición de ángulo.
60° + mq + 90° + 90° = 360°
Calcular la medición de Q.
Mq + 240° = 360°
mq = 120°
De la imagen, se puede ver que se trata de un ángulo obtuso, por lo que su medida debe ser mayor a 90°.
Respuesta: mq = 120°
La siguiente tabla resume los tipos especiales de cuadriláteros y algunas de sus propiedades.
| Nombre de Cuadrilátero | Cuadrilátero | Descripción |
| Paralelogramo | 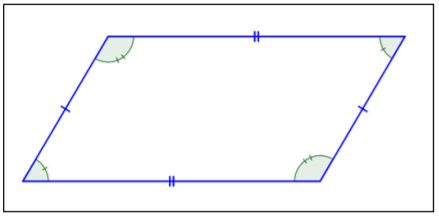 |
2 pares de lados paralelos. Los lados opuestos y los ángulos opuestos son congruentes. |
| Rectángulo | 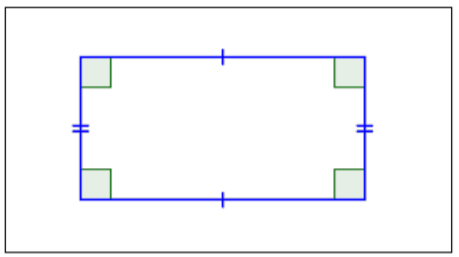 |
2 pares de lados paralelos. 4 ángulos rectos (90°). Los lados opuestos son paralelos y congruentes. Todos los ángulos son congruentes. |
| Cuadrado | 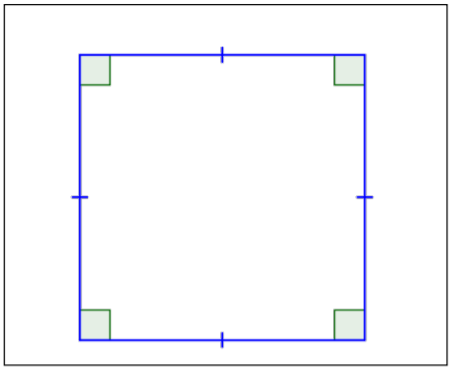 |
4 lados congruentes. 4 ángulos rectos (90°). Los lados opuestos son paralelos. Todos los ángulos son congruentes. |
| Trapecio | 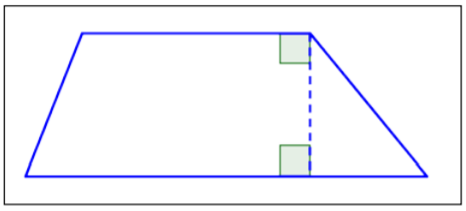 |
Sólo un par de lados opuestos es paralelo. |
Resumen
Un cuadrilátero es un nombre matemático para un polígono de cuatro lados. Los paralelogramos, cuadrados, rectángulos y trapecios son ejemplos de cuadriláteros. Estos cuadriláteros ganan su distinción en función de sus propiedades, incluyendo el número de pares de lados paralelos que tienen y sus medidas de ángulo y lado.
1. B) Todos los trapecios son cuadriláteros; los trapezoides son polígonos de cuatro lados, por lo que todos son cuadriláteros.
6.2.2: Perímetro y Área
- Encuentra el perímetro de un polígono.
- Encuentra el área de un polígono.
- Encontrar el área y perímetro de polígonos no estándar
Introducción
Perímetro y área son dos temas matemáticos importantes y fundamentales. Te ayudan a cuantificar el espacio físico y también proporcionan una base para matemáticas más avanzadas que se encuentran en álgebra, trigonometría y cálculo. El perímetro es una medida de la distancia alrededor de una forma y el área nos da una idea de cuánta superficie cubre la forma.
El conocimiento de área y perímetro es aplicado prácticamente por personas a diario, como arquitectos, ingenieros y diseñadores gráficos, y es matemática que es muy necesaria para la gente en general. Entender cuánto espacio tienes y aprender a encajar las formas exactamente te ayudará cuando pintas una habitación, compras una casa, remodelas una cocina o construyes una terraza.
Perimetral
El perímetro de una forma bidimensional es la distancia alrededor de la forma. Se puede pensar en envolver una cuerda alrededor de un triángulo. La longitud de esta cuerda sería el perímetro del triángulo. O caminando por el exterior de un parque, caminas a lo lejos del perímetro del parque. A algunas personas les resulta útil pensar “perimetral” porque el borde de un objeto es su borde y perimetral tiene la palabra “borde” en él.
Si la forma es un polígono, entonces puedes sumar todas las longitudes de los lados para encontrar el perímetro. Tenga cuidado de asegurarse de que todas las longitudes se midan en las mismas unidades. Se mide el perímetro en unidades lineales, que es unidimensional. Ejemplos de unidades de medida para la longitud son pulgadas, centímetros o pies.
Encuentra el perímetro de la figura dada. Todas las medidas indicadas son pulgadas.
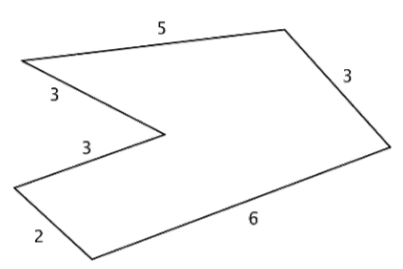
Solución
Dado que todos los lados se miden en pulgadas, solo agrega las longitudes de los seis lados para obtener el perímetro.
\(P = 5 + 3 + 6 + 2 + 3 + 3\)
Recuerda incluir unidades.
Respuesta:\(P = 22 \text{ inches}\)
Esto significa que una cuerda bien envuelta que recorre toda la distancia alrededor del polígono mediría 22 pulgadas de largo.
Encuentra el perímetro de un triángulo con lados de 6 cm, 8 cm y 12 cm.
Solución
Ya que todos los lados se miden en centímetros, solo agrega las longitudes de los tres lados para obtener el perímetro.
\(P = 6 + 8 + 12\)
Respuesta:\(P = 26 \text{ centimeters}\)
En ocasiones, necesitas usar lo que sabes de un polígono para encontrar el perímetro. Veamos el rectángulo en el siguiente ejemplo.
Un rectángulo tiene una longitud de 8 centímetros y un ancho de 3 centímetros. Encuentra el perímetro.
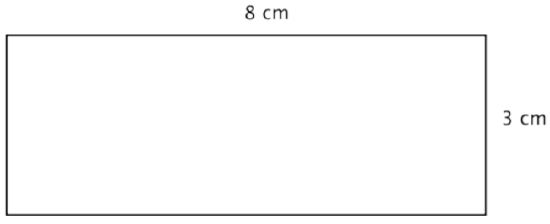
Solución
Al tratarse de un rectángulo, los lados opuestos tienen las mismas longitudes, 3 cm. y 8 cm. Suma las longitudes de los cuatro lados para encontrar el perímetro.
\(P = 3 + 3 + 8 + 8\)
Contestar\(P = 22 \text{ cm}\)
Observe que el perímetro de un rectángulo siempre tiene dos pares de lados de igual longitud. En el ejemplo anterior, también podrías haber escrito\(P = 2(3) + 2(8) = 6 + 16 = 22 \text{ cm}\). La fórmula para el perímetro de un rectángulo suele escribirse como\(P = 2l + 2w\), donde\(l\) está la longitud del rectángulo y\(w\) es el ancho del rectángulo.
Área de Paralelogramos
El área de una figura bidimensional describe la cantidad de superficie que cubre la forma. Se mide el área en unidades cuadradas de un tamaño fijo. Ejemplos de unidades de medida cuadradas son pulgadas cuadradas, centímetros cuadrados o millas cuadradas. Al encontrar el área de un polígono, se cuenta cuántos cuadrados de cierto tamaño cubrirán la región dentro del polígono.
Veamos un cuadrado de 4 x 4.
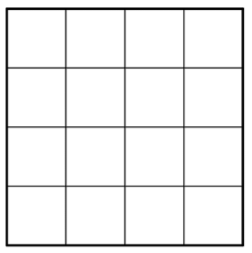
Se puede contar que hay 16 cuadrados, por lo que el área es de 16 unidades cuadradas. Contar 16 cuadrados no lleva demasiado tiempo, pero ¿qué pasa con encontrar el área si este es un cuadrado más grande o las unidades son más pequeñas? Podría llevar mucho tiempo contar.
Afortunadamente, puedes usar la multiplicación. Ya que hay 4 filas de 4 cuadrados, ¡puedes multiplicar\(4 \cdot 4\) para obtener\(16\) cuadrados! Y esto puede generalizarse a una fórmula para encontrar el área de un cuadrado con cualquier longitud,\(s\):\(\text{Area } = s \cdot s = s^2\).
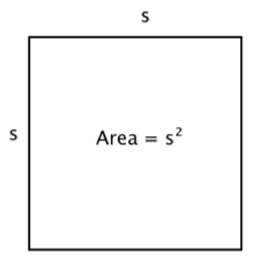
Puedes escribir “\(\text{in}^2\)” para pulgadas cuadradas y “\(\text{ft}^2\)” para pies cuadrados.
Para ayudarte a encontrar el área de las diferentes categorías de polígonos, los matemáticos han desarrollado fórmulas. Estas fórmulas te ayudan a encontrar la medición más rápidamente que simplemente contando. Las fórmulas que vas a ver están todas desarrolladas a partir del entendimiento de que estás contando el número de unidades cuadradas dentro del polígono. Echemos un vistazo a un rectángulo.
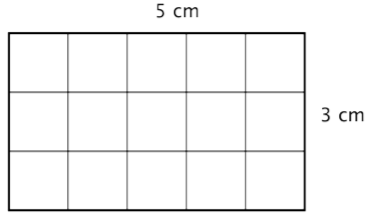
Se pueden contar los cuadrados individualmente, pero es mucho más fácil multiplicar 3 por 5 para encontrar el número más rápidamente. Y, de manera más general, el área de cualquier rectángulo se puede encontrar multiplicando longitud por ancho.
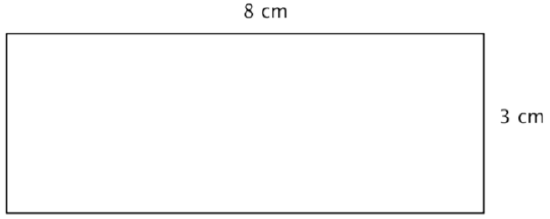
Un rectángulo tiene una longitud de 8 centímetros y un ancho de 3 centímetros. Encuentra la zona.
Solución
Comience con la fórmula para el área de un rectángulo, que multiplica la longitud por el ancho.
\(A = l \cdot w\)
Sustituye 8 por el largo y 3 por el ancho.
\(A = 8 \cdot 3\)
Asegúrese de incluir las unidades, en este caso, cm cuadrados.
Respuesta:\(A = 24 \text{ cm}^2\)
Se necesitarían 24 cuadrados, cada uno de 1 cm de lado, para cubrir este rectángulo.
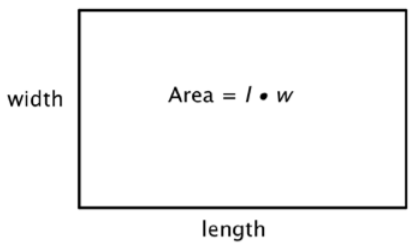
La fórmula para el área de cualquier paralelogramo (recuerde, un rectángulo es un tipo de paralelogramo) es la misma que la de un rectángulo:\(\text{Area } = l \cdot w\). Observe en un rectángulo, el largo y el ancho son perpendiculares. Esto también debería ser cierto para todos los paralelogramos. A menudo se usa base (b) para la longitud (de la base) y altura (h) para el ancho de la línea perpendicular a la base. Entonces, la fórmula para un paralelogramo generalmente se escribe,\(\text{Area } = b \cdot h\).
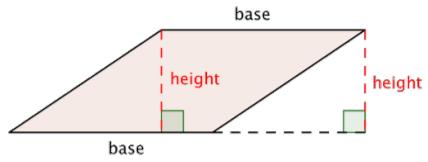
Encuentra el área del paralelogramo.
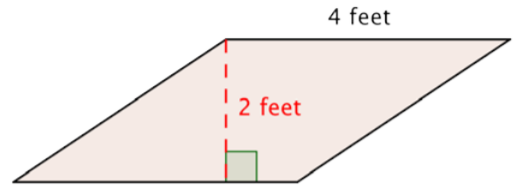
Solución
Comience con la fórmula para el área de un paralelogramo:\(\text{Area } = \text{base} \cdot \text{height}\).
\(A = b \cdot h\)
Sustituir los valores en la fórmula.
\(A = 4 \cdot 2\)
Multiplicar.
\(A = 8\)
Respuesta: El área del paralelogramo es\(8 \text{ ft}^2\).
Encuentra el área de un paralelogramo con una altura de 12 pies y una base de 9 pies.
Área de Triángulos y Trapezoides
La fórmula para el área de un triángulo se puede explicar mirando un triángulo rectángulo. Mire la imagen de abajo: un rectángulo con la misma altura y base que el triángulo original. ¡El área del triángulo es la mitad del rectángulo!
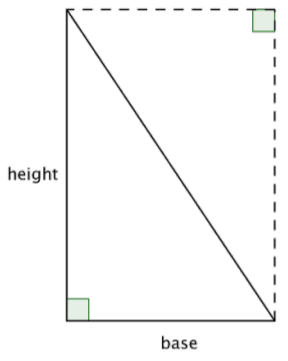
Dado que el área de dos triángulos congruentes es la misma que el área de un rectángulo, se puede llegar a la fórmula\(\text{Area } = \dfrac{1}{2}bh\) para encontrar el área de un triángulo.
Cuando se utiliza la fórmula para que un triángulo encuentre su área, es importante identificar una base y su altura correspondiente, que es perpendicular a la base.
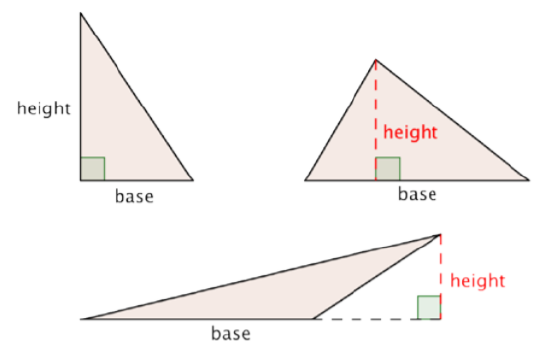
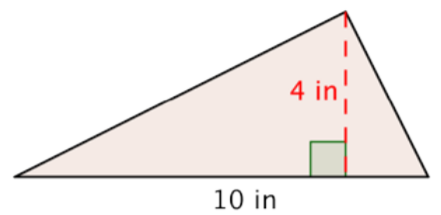
Un triángulo tiene una altura de 4 pulgadas y una base de 10 pulgadas. Encuentra la zona.
Solución
Comienza con la fórmula para el área de un triángulo.
\(A = \dfrac{1}{2}bh\)
Sustituye 10 por la base y 4 por la altura.
\(A = \dfrac{1}{2} \cdot (10) \cdot (4)\)
Multiplicar.
\(A = \dfrac{1}{2} \cdot 40\)
\(A = 20\)
Respuesta:\(A = 20 \text{ in}^2\)
Ahora veamos el trapecio. Para encontrar el área de un trapecio, tomar la longitud promedio de las dos bases paralelas y multiplicar esa longitud por la altura:\(A = \dfrac{(b_1 + b_2)}{2}h\).
A continuación se proporciona un ejemplo. Observe que la altura de un trapecio siempre será perpendicular a las bases (igual que cuando encuentre la altura de un paralelogramo).
Encuentra el área del trapecio.
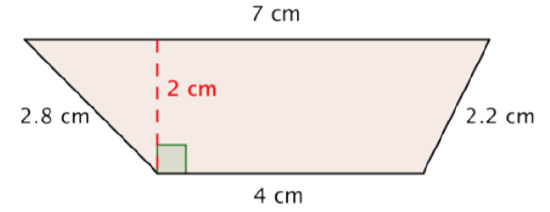
Solución
Comienza con la fórmula para el área de un trapecio.
\(A = \dfrac{(b_1 + b_2)}{2}h\)
Sustituye 4 y 7 por las bases y 2 por la altura, y encuentra A.
\(A = \dfrac{(4 + 7)}{2} \cdot 2\)
\(A = \dfrac{11}{2} \cdot 2\)
\(A = 11\)
Respuesta: El área del trapecio es\(11 \text{ cm}^2\)
Utilice las siguientes fórmulas para encontrar las áreas de diferentes formas.
cuadrado:\(A = s^2\)
rectángulo:\(A = l \cdot w\)
paralelogramo:\(A = b \cdot h\)
triángulo:\(A = \dfrac{1}{2}b \cdot h\)
trapecio:\(A = \dfrac{(b_1 + b_2)}{2}h\)
Trabajando con Perímetro y Área
A menudo es necesario encontrar el área o perímetro de una forma que no sea un polígono estándar. Los artistas y arquitectos, por ejemplo, suelen tratar con formas complejas. Sin embargo, incluso las formas complejas pueden considerarse compuestas por formas más pequeñas y menos complicadas, como rectángulos, trapecios y triángulos.
Para encontrar el perímetro de formas no estándar, aún encuentras la distancia alrededor de la forma al sumar la longitud de cada lado.
Encontrar el área de formas no estándar es un poco diferente. Es necesario crear regiones dentro de la forma para las que pueda encontrar el área y agregar estas áreas juntas. Echa un vistazo a cómo se hace esto a continuación.
Encuentra el área y perímetro del polígono.
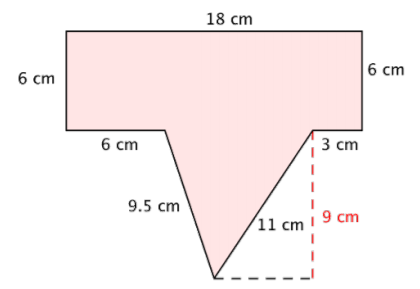
Solución
Para encontrar el perímetro, sumar las longitudes de los lados. Comience en la parte superior y trabaje en sentido horario alrededor de la forma.
\(P = 18 + 6 + 3 + 11 + 9.5 + 6 + 6\)
\(P = 59.5 \text{ cm}\)
Para encontrar el área, divida el polígono en dos regiones separadas y más simples. El área de todo el polígono será igual a la suma de las áreas de las dos regiones.
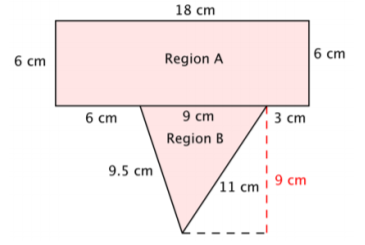
\(\text{Area of Polygon } = (\text{Area of A}) + (\text{Area of B})\)
La región A es un rectángulo. Para encontrar el área, multiplica la longitud (18) por la anchura (6).
\(\text{Area of Region }A = l \cdot w\)
\(= 18 \cdot 6\)
\(= 108\)
El área de la Región A es\(108 \text{ cm}^2\).
La región B es un triángulo. Para encontrar el área, usa la fórmula\(\dfrac{1}{2}bh\), donde la base es 9 y la altura es 9.
\(\text{Area of Region }B = \dfrac{1}{2}b \cdot h\)
\(= \dfrac{1}{2} \cdot 9 \cdot 9\)
\(= \dfrac{1}{2} \cdot 81\)
\(= 40.5\)
El área de la Región B es\(40.5 \text{ cm}^2\).
Sumar las regiones juntas.
\(108 \text{ cm}^2\)+\(40.5 \text{ cm}^2\) =\(148.5 \text{ cm}^2\).
Respuesta: Perímetro =\(59.5 \text{ cm}\)
Área =\(148.5 \text{ cm}^2\)
También puedes usar lo que sabes sobre perímetro y área para ayudar a resolver problemas sobre situaciones como comprar cercas o pintar, o determinar qué tan grande se necesita una alfombra en la sala de estar. Aquí hay un ejemplo de esgrima.
Rosie está plantando un jardín con las dimensiones que se muestran a continuación. Ella quiere poner una capa delgada y uniforme de mantillo sobre toda la superficie del jardín. El mantillo cuesta $3 el pie cuadrado. ¿Cuánto dinero tendrá que gastar en mantillo?
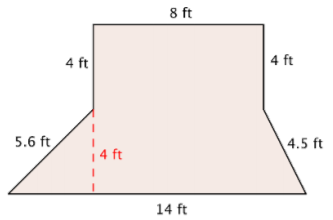
Solución
Esta forma es una combinación de dos formas más simples: un rectángulo y un trapecio. Encuentra el área de cada uno.
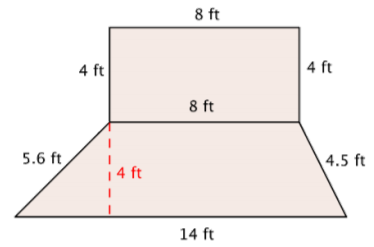
Encuentra el área del rectángulo.
\(A = l \cdot w\)
\(A = 8 \cdot 4\)
\(A = 32 \text{ ft}^2\)
Encuentra el área del trapecio.
\(A = \dfrac{(b_1 + b_2)}{2}h\)
\(A = \dfrac{(14 + 8)}{2} \cdot 4\)
\(A = \dfrac{22}{2} \cdot 4\)
\(A = 11 \cdot 4\)
\(A = 44 \text{ ft}^2\)
Añada las medidas.
\(32 \text{ ft}^2 + 44 \text{ ft}^2 = 76 \text{ ft}^2\)
Multiplica por $3 para saber cuánto tendrá que gastar Rosie.
\(76 \text{ ft}^2 \cdot $3 = $228\)
Respuesta: Rosie gastará 228 dólares para cubrir su jardín con mantillo.
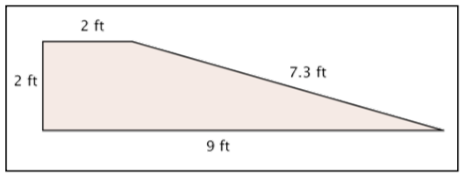
Encuentra el área de la forma dada.
Resumen
El perímetro de una forma bidimensional es la distancia alrededor de la forma. Se encuentra sumando todos los lados (siempre y cuando todos sean la misma unidad). El área de una forma bidimensional se encuentra contando el número de cuadrados que cubren la forma. Se han desarrollado muchas fórmulas para encontrar rápidamente el área de polígonos estándar, como triángulos y paralelogramos.
1. \(108 \text{ ft}^2\); la altura del paralelogramo es\(12\) y la base del paralelogramo es\(9\); el área es\(12\) veces\(9\), o\(108 \text{ ft}^2\).
2. \(11 \text{ ft}^2\); esta forma es un trapecio, por lo que puedes usar la fórmula\(A = \dfrac{(b_1 + b_2)}{2}h\) para encontrar el área:\(A = \dfrac{(2 + 9)}{2}\cdot 2\).
6.2.3: Círculos
- Identificar las propiedades de los círculos.
- Encuentra la circunferencia de un círculo.
- Encuentra el área de un círculo.
- Encuentra el área y perímetro de figuras geométricas compuestas.
Introducción
Los círculos son una forma común. Los ves por todas partes: ruedas en un automóvil, Frisbees pasando por el aire, discos compactos que entregan datos. Todos estos son círculos.
Un círculo es una figura bidimensional al igual que polígonos y cuadriláteros. Sin embargo, los círculos se miden de manera diferente a estas otras formas, incluso hay que usar algunos términos diferentes para describirlos. Echemos un vistazo a esta interesante forma.
Propiedades de Circles
Un círculo representa un conjunto de puntos, todos los cuales están a la misma distancia de un punto medio fijo. Este punto fijo se llama el centro. La distancia desde el centro del círculo hasta cualquier punto del círculo se llama radio.
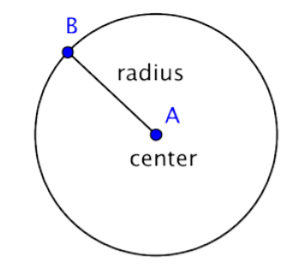
Cuando se juntan dos radios (el plural del radio) para formar un segmento de línea a través del círculo, se tiene un diámetro. El diámetro de un círculo pasa por el centro del círculo y tiene sus extremos en el círculo mismo.
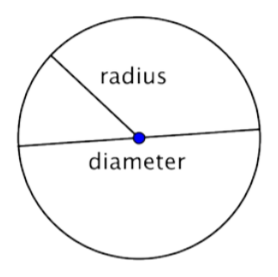
El diámetro de cualquier círculo es dos veces la longitud del radio de ese círculo. Se puede representar por la expresión 2r, o “dos veces el radio”. Entonces, si conoces el radio de un círculo, puedes multiplicarlo por 2 para encontrar el diámetro; esto también significa que si conoces el diámetro de un círculo, puedes dividirlo por 2 para encontrar el radio.
Encuentra el diámetro del círculo.
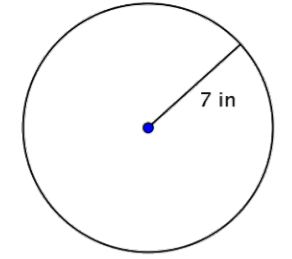
Solución
El diámetro es dos veces el radio, o 2r. El radio de este círculo es de 7 pulgadas, por lo que el diámetro es de 2 (7) = 14 pulgadas.
\(d = 2r\)
\(d = 2(7)\)
\(d = 14\)
Respuesta: El diámetro es de 14 pulgadas.
Encuentra el radio del círculo.
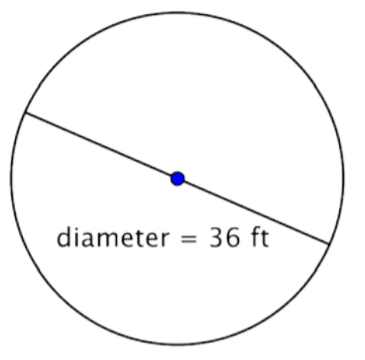
Solución
El radio es la mitad del diámetro, o\(\dfrac{1}{2}d\).
\(r = \dfrac{1}{2}d\)
\(r = \dfrac{1}{2}(36)\)
\(r = 18\)
El diámetro de este círculo es\(36 \text{ feet}\), entonces el radio es\(r = \dfrac{1}{2}(36) = 18 \text{ feet}\).
Respuesta: El radio es de 18 pies.
Circunferencia
La distancia alrededor de un círculo se llama circunferencia. (Recordemos, la distancia alrededor de un polígono es el perímetro.)
Una propiedad interesante sobre los círculos es que la relación entre la circunferencia de un círculo y su diámetro es la misma para todos los círculos. No importa el tamaño del círculo, la relación entre la circunferencia y el diámetro será la misma.
A continuación se proporcionan algunas medidas reales de diferentes artículos. Las mediciones son precisas al milímetro o cuarto de pulgada más cercano (dependiendo de la unidad de medida utilizada). Observe la relación entre la circunferencia y el diámetro de cada uno, aunque los artículos son diferentes, la proporción para cada uno es aproximadamente la misma.
| Artículo | Circunferencia (\(C\)) (redondeada a la centésima más cercana) | Diámetro (\(d\)) | Ratio\(\dfrac{C}{d}\) |
| Copa | 253 mm | 79 mm | \(\dfrac{253}{79} = 3.2025...\) |
| Trimestre | 84 mm | 27 mm | \(\dfrac{84}{27} = 3.1111...\) |
| Tazón | 37.25 in | 11.5 pulg | \(\dfrac{37.25}{11.75} = 3.1702...\) |
La circunferencia y el diámetro son medidas aproximadas ya que no existe una manera precisa de medir estas dimensiones exactamente. Si pudieras medirlas con mayor precisión, sin embargo, encontrarías que la proporción se\(\dfrac{C}{d}\) movería hacia\(3.14\) para cada uno de los ítems dados. El nombre matemático para la relación\(\dfrac{C}{d}\) es pi y está representado por la letra griega\(\pi\).
\(\pi\)es un decimal no terminante, no repetitivo, entonces es imposible escribirlo por completo? Los primeros 10 dígitos de\(\pi\) son 3.141592653; a menudo se redondea a 3.14 o se estima como la fracción\(\dfrac{22}{7}\). Obsérvese que tanto 3.14 como\(\dfrac{22}{7}\) son aproximaciones de\(\pi\), y se utilizan en cálculos donde no es importante ser precisos.
Ya que sabes que la relación de circunferencia a diámetro (o\(\pi\)) es consistente para todos los círculos, puedes usar este número para encontrar la circunferencia de un círculo si conoces su diámetro.
\(\dfrac{C}{d} = \pi, \text{ so } C = \pi d\)
También, desde\(d = 2r\), entonces\(C = \pi d = \pi (2r) = 2 \pi r\).
Para encontrar la circunferencia (\(C\)) de un círculo, utilice una de las siguientes fórmulas:
Si conoce el diámetro (\(d\)) de un círculo:\(C = \pi d\))
Si conoce el radio (\(r\)) de un círculo:\(C = 2 \pi r\))
Encuentra la circunferencia del círculo.
Solución
Para calcular la circunferencia dada un diámetro de 9 pulgadas, usa la fórmula\(C = \pi d\). Utilice 3.14 como aproximación para\(\pi\). Ya que estás usando una aproximación para\(\pi\), no puedes dar una medida exacta de la circunferencia. En su lugar, usa el símbolo\(≈\) para indicar “aproximadamente igual a”.
\(C = \pi d\)
\(C = \pi \cdot 9\)
\(C ≈ 3.14 \cdot 9\)
\(C ≈ 28.26\)
Respuesta: La circunferencia es\(9\pi\) o aproximadamente\(28.26 \text{ inches}\).
Encuentra la circunferencia de un círculo con un radio de 2.5 yardas.
Solución
Para calcular la circunferencia de un círculo dado un radio de 2.5 yardas, usa la fórmula\(C = 2 \pi r\). Utilice 3.14 como aproximación para\(\pi\).
\(C = 2 \pi r\)
\(C = 2 \pi \cdot 2.5\)
\(C = \pi \cdot 5\)
\(C ≈ 3.14 \cdot 5\)
\(C ≈ 15.7\)
Respuesta: La circunferencia es\(5\pi\) o aproximadamente\(15.7 \text{ yards}\).
Un círculo tiene un radio de 8 pulgadas. ¿Cuál es su circunferencia, redondeada a la pulgada más cercana?
Área
Pi,\(\pi\), es un número importante en geometría. Ya lo has usado para calcular la circunferencia de un círculo. También usas\(\pi\) cuando estás averiguando el área de un círculo.
Para encontrar el área (\(A\)) de un círculo, use la fórmula:\(A = \pi r^2\)
Encuentra el área del círculo.
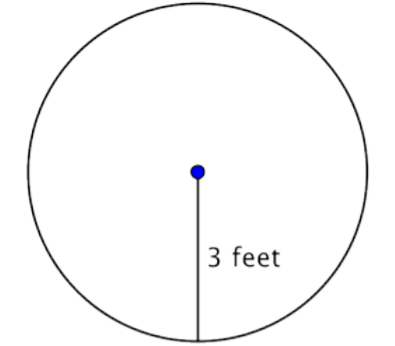
Solución
Para encontrar el área de este círculo, usa la fórmula\(A = \pi r^2\). Recuerda escribir la respuesta en términos de unidades cuadradas, ya que estás encontrando el área.
\(A = \pi r^2\)
\(A = \pi \cdot 3^2\)
\(A = \pi \cdot 9\)
\(A = 3.14 \cdot 9\)
\(A = 28.26\)
Responder El área es\(9\pi\) o aproximadamente\(28.26 \text{ feet}^2\).
Un botón tiene un diámetro de 20 milímetros. ¿Cuál es el área del botón? Usar 3.14 como aproximación de\(\pi\).
Figuras compuestas
Ahora que ya sabes calcular la circunferencia y el área de un círculo, puedes usar este conocimiento para encontrar el perímetro y el área de figuras compuestas. El truco para descubrir este tipo de problemas es identificar formas (y partes de formas) dentro de la figura compuesta, calcular sus dimensiones individuales y luego sumarlas juntas.
Por ejemplo, mira la imagen de abajo. ¿Es posible encontrar el perímetro?
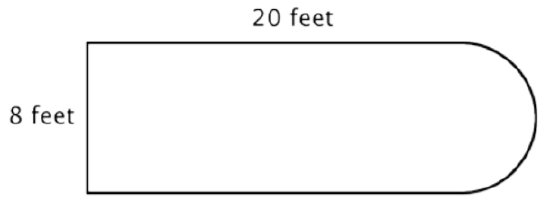
El primer paso es identificar figuras más simples dentro de esta figura compuesta. Se puede descomponer en un rectángulo y un semicírculo, como se muestra a continuación.
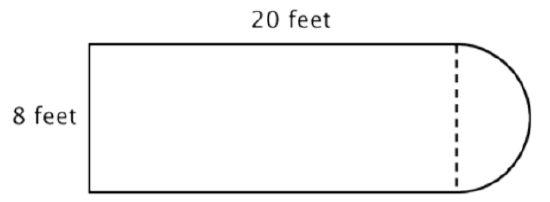
Sabes encontrar el perímetro de un rectángulo, y sabes cómo encontrar la circunferencia de un círculo. Aquí, el perímetro de los tres lados sólidos del rectángulo es de 8 + 20 + 20 = 48 pies. (Tenga en cuenta que solo tres lados del rectángulo se agregarán al perímetro de la figura compuesta porque el otro lado no está en un borde; ¡está cubierto por el semicírculo!)
Para encontrar la circunferencia del semicírculo, usa la fórmula\(C = \pi d\) con un diámetro de 8 pies, luego toma la mitad del resultado. La circunferencia del semicírculo es\(4 \pi\), o aproximadamente 12.56 pies, por lo que el perímetro total es de aproximadamente 60.56 pies.
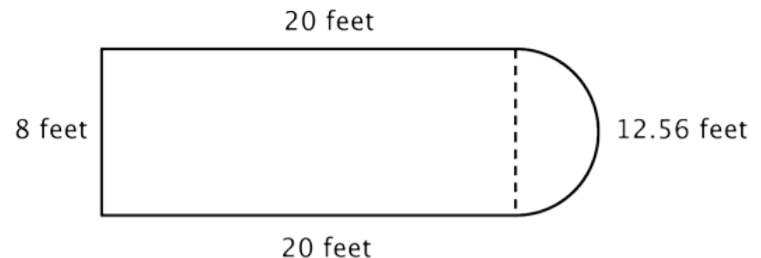
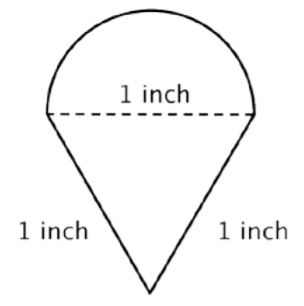
Encuentra el perímetro (a la centésima más cercana) de la figura compuesta, conformada por un semicírculo y un triángulo.
Solución
Identificar formas más pequeñas dentro de la figura compuesta. Esta figura contiene un semicírculo y un triángulo.
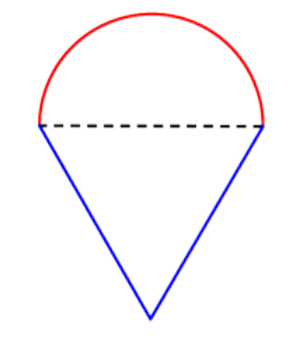
Encuentra la circunferencia del círculo. Luego divide por 2 para encontrar la circunferencia del semicírculo.
\(\text{Diameter }(d) = 1\)
\(C = \pi d\)
\(C = \pi (1)\)
\(C = \pi\)
\(\text{Circumference of semicircle } = \dfrac{1}{2} \pi\)o aproximadamente\(1.57 \text{ inches}\)
Encuentra el perímetro total sumando la circunferencia del semicírculo y las longitudes de las dos patas. Dado que nuestra medición de la circunferencia del semicírculo es aproximada, el perímetro también será una aproximación.
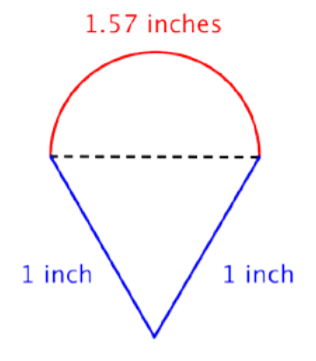
\(1 + 1 + \dfrac{1}{2} \pi ≈ 3.57 \text{ inches}\)
Recordemos, utilizamos las unidades originales con perímetro.
Respuesta: Aproximadamente\(3.57 \text{ inches}\)
Encuentra el área de la figura compuesta, compuesta por tres cuartas partes de círculo y un cuadrado, a la centésima más cercana.
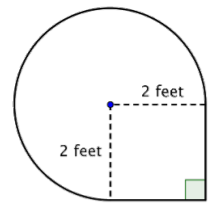
Solución
Identificar formas más pequeñas dentro de la figura compuesta. Esta figura contiene una región circular y un cuadrado. Si encuentras el área de cada uno, puedes encontrar el área de toda la figura.
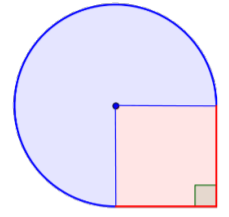
Encuentra el área de la plaza.
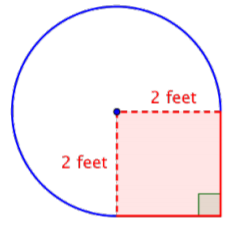
\(\text{Area of square} = s^2\)
\(= (2)^2\)
\(= 4 \text{ ft}^2\)
Encuentra el área de la región circular. El radio es\(2 \text{ feet}\).
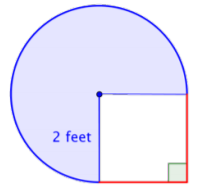
Tenga en cuenta que la región es\(\dfrac{3}{4}\) de un círculo completo, por lo que debe multiplicar el área del círculo por\(\dfrac{3}{4}\). Utilice 3.14 como aproximación para\(\pi\).
\(\text{Area of full circle} = \pi r^2\)
\(= \pi (2)^2\)
\(= 4 \pi \text{ ft}^2\)
\(\text{Area of region} = \dfrac{3}{4} \cdot 4 \pi \)
\(= 3 \pi\)
\(≈ 3 \cdot 3.14 \text{ ft}^2\)
Esto es aproximadamente\(9.42 \text{ feet}^2\).
Sumar las dos regiones juntas. Dado que su medida del área de la circular es aproximada, el área de la figura será una aproximación también.
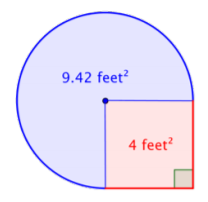
\(4 \text{ feet}^2 + 3 \pi \text{ feet}^2 =\)aproximadamente\(13.42 \text{ feet}^2\)
Recordemos, utilizamos unidades cuadradas para el área.
Respuesta: El área es aproximadamente\(13.42 \text{ feet}^2\).
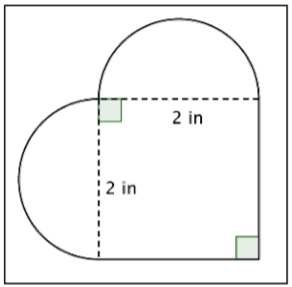
¿Cuál es el área (a la centésima más cercana) de la figura que se muestra a continuación? (Ambas regiones redondeadas son semicírculos).
Resumen
Los círculos son una forma geométrica importante. La distancia alrededor de un círculo se llama circunferencia, y el espacio interior de un círculo se llama área. Calcular la circunferencia y el área de un círculo requiere un número llamado pi (\(\pi\)), que es un decimal no terminante y no repetitivo. Pi a menudo se aproxima por los valores 3.14 y\(\dfrac{22}{7}\). Puede encontrar el perímetro o el área de formas compuestas, incluidas las formas que contienen secciones circulares, aplicando las fórmulas de circunferencia y área donde corresponda.
- \(50 \text{ inches}\); si el radio es\(8 \text{ inches}\), la fórmula correcta para la circunferencia cuando se da el radio es\(C = 2 \pi r\). La respuesta correcta es\(50 \text{ inches}\).
- \(314 \text{ mm}^2\); el diámetro es\(20 \text{ mm}\), por lo que el radio debe ser\(10 \text{ mm}\). Entonces, usando la fórmula\(A = \pi r^2\), encuentras\(A = \pi \cdot 10^2 = \pi \cdot 100 ≈ 314 \text{ mm}^2\).
- \(7.14 \text{ in}^2\); imagina que los dos semicírculos se juntan para crear un círculo. El radio del círculo es\(1 \text{ inch}\); esto significa que el área del círculo es\(\pi r^2 = \pi \cdot 1^2 = \pi\). El área de la plaza es\(2 \cdot 2 = 4\). Sumando esos rendimientos juntos\(7.14 \text{ in}^2\).


