1.6 Chapter 1 Study Guide
- Page ID
- 152947
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- natural numbers (\( \mathbb{N}\)): The "counting" numbers, nonnegative whole numbers, aka \(0, 1, 2, 3, ...\) forever.
- integers (\( \mathbb{Z}\)): All of the whole numbers, including negative numbers. These also go on forever but in both directions, \(..., -3, -2, -1, 0, 1, 2, 3, ...\).
- rational numbers (\(\mathbb{Q}\)): All numbers that can be written as a ratio of two integers, so things like \(\frac{1}{2}, -\frac{7}{5}, \frac{27}{4001},\) etc. These include integers, because we can write \( 4 = \frac{4}{1} \) if we want. Decimal representations of rational numbers either end, like \(1.5\), or repeat forever, like \(1.33333...\).
- real numbers (\(\mathbb{R})\): All of the above numbers, together with irrational numbers, such as \( \sqrt{2}, \sqrt{5}, \pi, e, \) etc. These numbers' decimal representations never end or have a repeating pattern.
- commutative: An operation is commutative if it doesn't matter what order you do it in. Addition and multiplication are commutative since \( a+b = b+a\) and \(ab = ba\), but subtraction and division aren't!
- factor: A number's factors are the numbers that can be multiplied to produce it. For example, factors of \(12\) are \(\pm 1, \pm 12, \pm 2, \pm 6, \pm 3, \pm 4\).
- sum: the result of an addition.
- difference: the result of a subtraction.
- product: the result of a multiplication.
- quotient: the result of a division. The number you divide BY is the divisor. The number getting divided is the dividend.
- strictly less than / less than or equal to: symbols are \( < \) and \(\leq\) respectively. For example, \(3 < \pi\).
- strictly greater than / greater than or equal to: symbols are \( > \) and \( \geq \) respectively. For example, if we say \(x \geq 4\), that means \(x\) could be equal to 4 or anything larger than that.
- numerator / denominator: The top of a fraction is the numerator. The bottom of a fraction is the denominator.
- reciprocal: The reciprocal of \( \frac{a}{b} \) is \( \frac{b}{a} \).
- compound fraction: A fraction that has fractions inside of its numerator or denominator or both.
- least common multiple (LCM): The smallest number that all of a set of numbers divide evenly into. Example: the LCM of \(3, 4,\) and \(6\) is \(12\). This is used when getting a common denominator.
- percent: a proportion out of 100. Example: 20% is \(20/100 = \frac{1}{5} = 0.2\).
- power / exponent: \( a^k\) is "\(a\) raised to the power \(k\)" and can be thought of as multiplying \(a\) by itself a total of \(k\) times. The base is \(a\), and the exponent is \(k\).
- radical / root: \(\sqrt{a} = b \) means \( b\) is the positive number such that \(b^2 = a\). Similarly, \(\sqrt[3]{a} = b\) means \(b^3 = a\), and so on.
- scientific notation: a number is in scientific notation if it is written as X.XXXX times an appropriate power of 10. Examples: \(1,234,000 = 1.234 \times 10^6 \) and \(0.00001234 = 1.234 \times 10^{-5}\). If the exponent is positive, it's a large number. If the exponent is negative, it's a tiny number.
- Subtraction is the same as adding a negative number, and adding negative numbers is the same as taking the difference (the sign of the answer matches the sign of the bigger number). For example, \(2 - 3 = 2 + (-3) = -1 \).
- Multiplication distributes over sums and differences, like \(2(1+3) = 2\cdot 1 + 2 \cdot 3 = 2+6 = 8\), but you have to be careful when distributing a negative number. For example, \( -3(a+b) = -3a - 3b\).
- Positive \(\times\) positive = positive. Negative \( \times\) negative = positive. Positive \( \times\) negative = negative. The same applies to division!
0. Parentheses first. Working from the innermost outward, completely take care of expressions inside parentheses.
1. Exponents (powers). If numbers are being raised to a power, compute those first.
2. Multiplication/Division. Working left to right, compute any multiplications and divisions.
3. Addition/Subtraction. Working left to right, compute any sums and differences.
Example:
\[ 2(3+(4-2)^2) - \frac{(3+1)}{4} = 2( 3+ (2)^2) - \frac{4}{4} = 2(3+4) - \frac{4}{4} = 2(7) - \frac{4}{4} = 14 - 1 = 13 \notag \]
- To multiply fractions, multiply across the top and multiply across the bottom: \( \frac{a}{b} \cdot \frac{c}{d} = \frac{ab}{cd} \).
- To divide fractions, multiply by the reciprocal: \( \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \).
- To add or subtract fractions, get a common denominator for all fractions, and then add or subtract (using parentheses if necessary).

When rounding to a certain place, look at the digit directly to the right. If it's less than 5, round down. If it's 5 and up, round up.
- Adding and subtracting: arrange vertically with decimal points lined up and add/subtract down columns as usual:
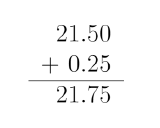
- Multiplying: ignore the decimal points and multiply the numbers, then count up the total number of decimal places and put the new point that far into the product. Example: for \( 1.5 \cdot 0.4 \), first multiply \(15 \cdot 4 = 60 \), then each number had one decimal place, so put the point two places in to get \(0.60\) as the answer.
- Powers of 10 trick: If multiplying by \( 10^k\), move the decimal point \(k\) steps to the right, adding zeros into the spaces. Example: \(4.2 \cdot 10^3 = 4200\). If dividing by \(10^k\) (aka multiplying by \(10^{-k}\)), move the decimal point \(k\) steps to the left, adding zeros if needed. Example: \( 4.2 \cdot 10^{-3} = 0.0042 \).
| Fraction | Decimal |
| \( \frac{1}{2} \) | \(0.5\) |
| \( \frac{1}{3}\) | \(0.\overline{3}\), which means the 3s go on forever like \(0.33333...\) |
| \( \frac{2}{3} \) | \(0.\overline{6}\), which due to rounding rules rounds to things like \(0.6667\) |
| \( \frac{1}{4} \) | \( 0.25 \), like how 25 cents is a quarter of a dollar |
| \( \frac{3}{4} \) | \( 0.75 \) |
| \( \frac{1}{5} \) | \( 0.2 \), which you can remember as \(0.20\) because 20 is one-fifth of a 100 |
| \( \frac{1}{8} \) | \( 0.125 \) |
| \( \frac{3}{2}, \frac{5}{2}, \frac{7}{2}, ... \) | \(1.5 , 2.5, 3.5, ...\), which are just like finding mixed numbers from improper fractions |
- To find XX% of a quantity, convert to a decimal by moving the point two steps to the left, getting 0.XX, and then multiply. Example: 10% of 30 would be \(0.1 (30) = 3\).
- To convert from a ratio to a percent, just divide \( \frac{\text{part}}{\text{whole}} \) and multiply by 100. Example: 2 out of 5 students come to office hours means \(\frac{2}{5}\cdot 100 = 0.4 \cdot 100 = 40\)% of students come to office hours.
| \( a^b a^c = a^{b+c} \) | \( \dfrac{a^b}{a^c} = a^b a^{-c} = a^{b-c} \) | \( (a^b)^c = a^{bc} \) | \( a^{-n} = \frac{1}{a^n} \) and \( \frac{1}{a^{-n}} = a^n \) |
| \( a^0 = 1 \) | \( a^1 = a\) | \( 0^n = 0 \) | \( 1^n = 1\) |
| \( (ab)^c = a^c b^c \) | \( \textcolor{red}{(a+b)^c \neq a^c + b^c} \) | \(\text{negative}^{\text{even power}} = \text{positive}\) | \( \text{negative}^{\text{odd power}} = \text{negative} \) |
| \( \sqrt[n]{0} = 0\) | \( \sqrt[n]{1} = 1 \) | \(( \sqrt[n]{a})^n = a\) | \( \sqrt[n]{a} = a^{\frac{1}{n}} \) |
| \( (\sqrt[n]{a})^m = \sqrt[n]{a^m} = a^{\frac{m}{n}} \) | \( \sqrt[n]{ab}= \sqrt[n]{a}\sqrt[n]{b} \) | \( \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \) | \( \textcolor{red}{ \sqrt[n]{a+b} \neq \sqrt[n]{a} + \sqrt[n]{b} }\) |
| \(\sqrt{4} = 2\) | \( \sqrt{400} = 20 \) |
| \(\sqrt{9} = 3 \) | \( \sqrt{3600} = 60 \), etc. |
| \(\sqrt{16} = 4 \) | \( \sqrt{10000} = 100 \), etc. |
| \( \sqrt{25} = 5 \) | \( \sqrt[3]{8} = 2 \) |
| \( \sqrt{36} = 6 \) | \( \sqrt[3]{27} = 3 \) |
| \( \sqrt{49} = 7 \) | \( \sqrt[3]{64} = 4 \) |
| \( \sqrt{64} = 8 \) | \( \sqrt[3]{125}= 5 \) |
| \( \sqrt{81} = 9 \) | \( \sqrt[3]{1000} = 10 \) |
| \(\sqrt{100} = 10 \) | \( \sqrt[4]{16} = 2 \) |
| \( \sqrt{121} = 11 \) | \( \sqrt[4]{81} = 3 \) |
| \( \sqrt{144} = 12 \) | \( \sqrt[4]{10000} = 10 \) |
- If two fractions have the same denominator, compare the numerators. The bigger numerator gives a larger fraction. Example: \(\frac{2}{3} > \frac{1}{3} \).
- If they have the same numerator, compare the denominators. The bigger denominator gives a smaller fraction. Example: \( \frac{1}{4} < \frac{1}{2} \).
- If they have different numerators and denominators, find a common denominator and then compare the new numerators. Example: \( \frac{5}{4} = \frac{15}{12}\) is smaller than \( \frac{4}{3} = \frac{16}{12} \).


