6.1E Exercises
- Page ID
- 155176
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Algebraically, identify the domain and any roots and vertical asymptotes of the rational functions.
1. \( f(x) = \dfrac{x}{x+1} \)
2. \( g(x) = \dfrac{ 2x^2 - 3x}{x-4} \)
3. \( h(x) = \dfrac{5}{x^2 + 1} \)
4. \( p(x) = \dfrac{3x^2 - 5x + 2}{x^2 - 4x + 4} \)
5. \( q(x) = \dfrac{x^3 - x^2}{2x^2+x-6} \)
6. \( r(x) = \dfrac{ 2x}{x^2-9} \)
7. \( C(t) = \dfrac{t^2 - 2t+1}{t^3 - 8} \)
- Answer
-
- Domain: all real numbers \(x \neq -1\). Roots: \(x = 0\). V.A. \(x = -1\).
- Domain: all real numbers \(x \neq 4 \). Roots: \(x = 0, \frac{3}{2} \). V.A. \( x = 4\).
- Domain: all real numbers. Roots: none. No V.A.s.
- Domain: all real numbers \(x \neq 2 \). Roots: \( x = \frac{2}{3}, 1 \). V.A. \( x = 2 \).
- Domain: all real numbers \(x \neq \frac{3}{2}, -2 \). Roots: \( x = 0, 1 \). V.A.s \(x = \frac{3}{2} \) and \( x = -2\).
- Domain: all real numbers \( x \neq \pm 3\). Roots: \( x = 0\). V.A.s \(x = -3\) and \(x = 3\).
- Domain: all real numbers \(x \neq 2 \). Roots: \( x = 1\). V.A. \( x = 2 \).
By looking at the graph, identify any roots, vertical asymptotes, and horizontal asymptotes of the rational function. Then match each graph to its potential function.
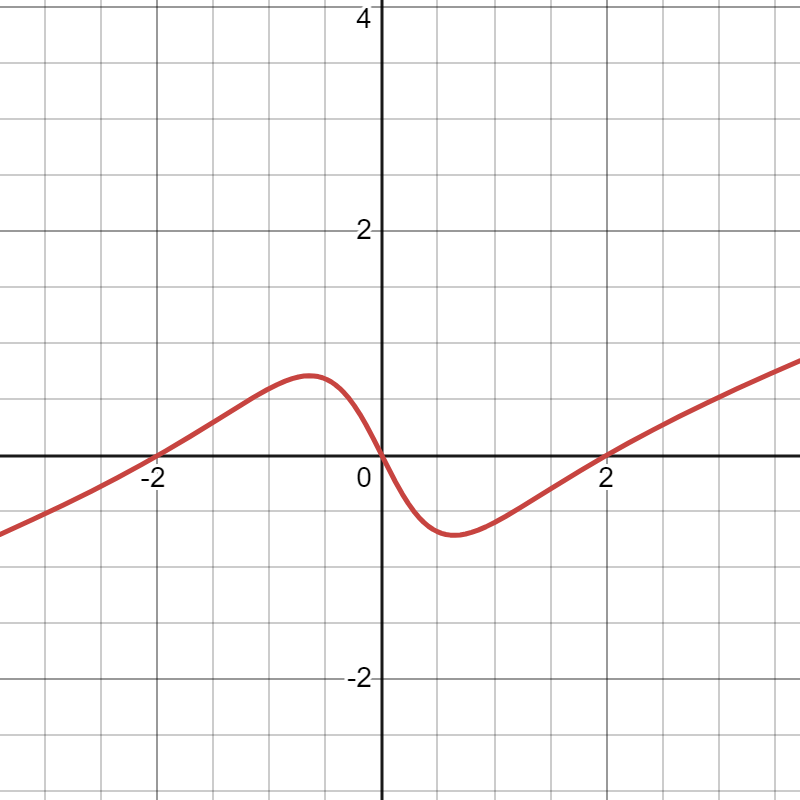 |
 |
 |
 |
| 1. | 2. | 3. | 4. |
A. \( f(x) = \dfrac{x^2+1}{(x+1)^2(x-1)} \)
B. \( f(x) = \dfrac{x^3-4x}{3x^2+2} \)
C. \( f(x) = \dfrac{ 2x+4}{x+5} \)
D. \( f(x) = \dfrac{ 2x}{x^2-9} \)
- Answer
-
1. No V.A. or H.A., roots at \( x = -2, 0, 2\). Goes with B.
2. Root at \(x = 0\). V.A.s \( x = -3\) and \(x = 3\). H.A. \(y = 0\). Goes with D.
3. Root at \(x = -2\). V.A. \(x = -5\). H.A. \(y = 2\). Goes with C.
4. No roots. V.A.s \(x = -1\) and \(x = 1\). H.A. \(y = 0\). Goes with A.
If the degree of the numerator is greater than or equal to the degree of the denominator, write \( \dfrac{ p(x)}{d(x)} \) in the form \( q(x) + \dfrac{r(x)}{d(x)} \). If not, use partial fractions to write as a sum of terms with linear factors in the denominators.
1. \( g(x) = \dfrac{ 2x^2 - 3x}{x-4} \)
2. \( p(x) = \dfrac{3x^2 - 5x + 2}{x^2 - 4x + 4} \)
3. \( r(x) = \dfrac{ 2x}{x^2-9} \)
4. \( q(x) = \dfrac{2x^3 - 2x^2+18}{2x^2+x-6} \)
5. \( f(x) = \dfrac{6 x^2}{(x-2)(x^2 - 1)} \)
6. \( h(x) = \dfrac{ 2x + 1}{x^2 -5x + 6} \)
- Answer
-
1. \( 2x+5 + \dfrac{20}{x-4} \)
2. \( 3 + \dfrac{7x-10}{x^2-4x+4}\)
3. \( \dfrac{1}{x+3} + \dfrac{1}{x-3} \)
4. \( x-\frac{3}{2} + \dfrac{ \frac{15}{2}x + 9}{2x^2+x-6} \)
5. \( -\dfrac{3}{x-1}+\dfrac{1}{x+1} + \dfrac{8}{x-2} \)
6. \( \dfrac{7}{x-3} - \dfrac{5}{x-2} \)
Solve the inequalities.
1. \( x^3 - 2x^2 - 3x \geq 0 \)
2. \( x^3 < 9x \)
3. \( \dfrac{x}{x^2-1} + \dfrac{1}{x+1} \leq 0 \)
4. \( \dfrac{1}{x} > \dfrac{2}{x-1} \)
- Answer
-
- \( [-1, 0] \cup [3, \infty) \)
- ALERT: you can't just divide both sides by \(x\) because \(x\) can take negative and positive values, so you won't know whether to flip the inequality sign! \( (-\infty, -3)\cup (0,3) \)
- \( (-\infty, -1) \cup \left[ \frac{1}{2}, 1\right) \)
- \( \left(-\infty, -1 \right) \cup (0,1) \)
If a function is defined by a rational expression that is not fully reduced, for example,
\[ r(x) = \frac{ x^2 - 2x + 1}{x^2 +2x - 3} = \frac{ (x-1)(x-1)}{(x-1)(x+3)} \notag\]
then its domain does not include the problem value \(x = 1\) that causes the denominator to be zero (and of course, we can't allow \(x = -3\) either). However, this function doesn't have a vertical asymptote at \(x = 1\) like it does at \(x = -3\)! For all purposes besides the actual problem value, the function will behave exactly like the function defined by the simplified rational expression,
\[ f(x) = \frac{ x-1}{x+3} \notag \]
Both are graphed below. The graph of \(r(x)\) has a hole (or removable discontinuity) at \(x = 1\), but otherwise it looks just like the graph of \(f(x)\).


Now, for the functions given, identify their domain issues, and indicate whether each problem value yields a hole or a vertical asymptote. Find the fully reduced rational function \(f \) whose graph will match (apart from holes).
1. \( r(x) = \dfrac{ x^2 + 6x + 5}{2x^2+3x+1} \)
2. \( r(x) = \dfrac{ x^3 - x}{2x^2 + 4x} \)
3. \( r(x) = \dfrac{ (x+1)(x-2)(x+3)}{ (x-1)(x+1)(x-2)(x+2) } \)
- Answer
-
1. Domain: \( x \neq -\frac{1}{2}, -1\). Vertical asymptote \(x = -\frac{1}{2} \) and hole at \(x = -1\). \(f(x) = \dfrac{ x+5}{2x+1} \).
2. Domain: \(x \neq 0, -2\). Vertical asymptote \(x = -2\), hole at \(x = 0\). \( f(x) = \dfrac{ x^2 - 1}{2(x+2)} \).
3. Domain: \(x \neq \pm 1, \pm 2\). Vertical asymptotes \( x = 1\) and \(x = -2\). Holes at \(x = -1, 2 \). \( f(x) = \dfrac{ x+3}{(x-1)(x+2)} \).

