7.1E Exercises
- Page ID
- 155685
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)(Note: Most of these problems come from Section 6.3E, except for the transformation and sketching material.)
Answer True/False. If False, justify or find the error.
- The function \( f(x) = x^{\frac{1}{2} }\) is exponential with base \( \frac{1}{2} \).
- The function \( f(x) = \left( \frac{1}{2} \right)^x \) is exponential with base \( \frac{1}{2} \).
- The expression \( \left( \frac{1}{2} \right)^x \) is equivalent to the expression \( \frac{1}{2^x} \).
- The function \( f(x) = 5^x \) is exponential with base 5.
- The function \( f(x) = 5^{-x} \) is exponential with base 5.
- The function \( f(x) = 5^{-x} \) is exponential with base \( \frac{1}{5} \).
- The function \( f(x) = 3^x\) is increasing.
- The function \( f(x) = \left(\frac{1}{3}\right)^x \) is increasing.
- The function \( f(x) = \left(\frac{1}{3}\right)^x \) is decreasing.
- For \( f(x) = 3^x\), we have \(f(0) = 3 \).
- For \( f(x) = 3^x\), we have \(f(0) = 1 \).
- For \( f(x) = 3^x\), we have \(f(1) = 3 \).
- The function \( f(x) = e^x \) can take negative values. That is, there exists some \(x\) such that \(f(x) < 0 \).
- The function \( f(x) = 3^x\) can take negative values.
- Answer
-
- F, the variable isn't in the exponent.
- T
- T
- T
- F, rewrite \( 5^{-x} \) as \( \left( \frac{1}{5} \right)^x \) to see the base.
- T
- T
- F, when the base is less than 1, the function is decreasing (downhill behavior).
- T
- F, \( f(0) = 3^0 = 1 \).
- T
- T
- F, exponential functions like this never take negative values (stay above the \(x\)-axis).
- F, same reason.
Answer True/False. If False, justify or find the error.
- The graph of \(f(x) = a^x\) passes through \( (0,1)\) for any base with \(a > 0\) and \(a \neq 1\).
- The graph of \( f(x) = 2^x\) is increasing.
- The graph of \( f(x) = \left( \frac{4}{5} \right)^x \) is decreasing.
- The graph of \( f(x) = \left( \frac{5}{4} \right)^x \) is decreasing.
- As \(x \rightarrow \infty\), the graph of \( f(x) = 5^x\) is steeper (faster growing) than the graph of \(g(x) = 10^x \).
- As \(x \rightarrow \infty\), the graph of \( g(x) = 10^x\) is steeper (faster growing) than the graph of \( f(x) = 5^x\).
- The graph of \( f(x) = e^x\) is increasing.
- The graph of \(f(x) = e^x \) is steeper than the graph of \(g(x) = 3^x \), for \(x > 0\).
- The graph of \( f(x) = 6^x \) passes through \( (1,6) \).
- The graph of \( f(x) = 6^x \) passes through \( \left(-1, \frac{1}{6} \right) \).
- The graph of \(f(x) = 6^x \) passes through \( (6, 1) \).
- The graph of \( f(x) = e^x\) passes below the \(x\)-axis.
- The graph of \(f(x) = a^x \) passes through \( (1,a)\) for any base \(a\).
- The graph of \( f(x) = 5^{-x} \) is the reflection across the \(y\)-axis of the graph of \( g(x) = 5^x\).
- The graph of \( f(x) = \left( \frac{1}{7} \right)^x \) is the reflection across the \(y\)-axis of the graph of \( g(x) = 7^x \).
- Answer
-
- T
- T
- T
- F, the base \( \frac{5}{4} > 1 \) so it's increasing.
- F, bigger base gives faster growth.
- T
- T
- F, \(e \approx 2.71...\) is less than 3, so \(g\) has the larger base and thus faster growth.
- T
- T
- F, \( f(6) = 6^6 \).
- F, as mentioned, these exponential functions are always positive.
- T
- T
- T
By analyzing signal points like \( (1,a)\) and \( \left(-1, \frac{1}{a}\right) \) and using your knowledge of exponential function graphs, match the graphs to their functions.
 |
 |
 |
 |
| 1. | 2. | 3. | 4. |
| \( f(x) = e^x\) | \( g(x) = \left(\frac{1}{3}\right)^x \) | \( h(x) = 7^x\) | \( p(x) = 4^{-x} \) |
- Answer
-
- \(h\)
- \(p\)
- \(f\)
- \( g\)
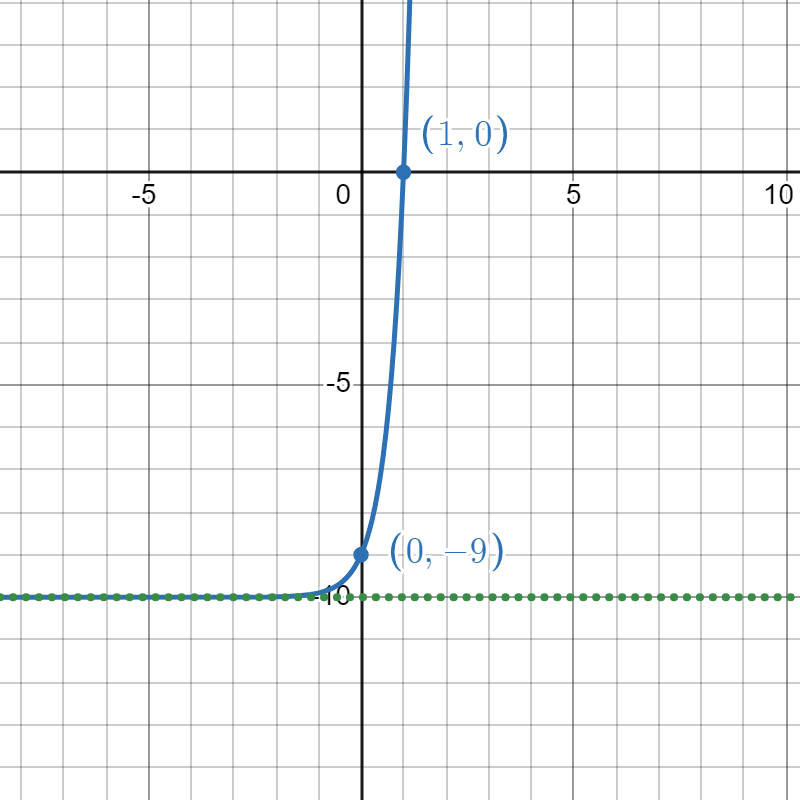
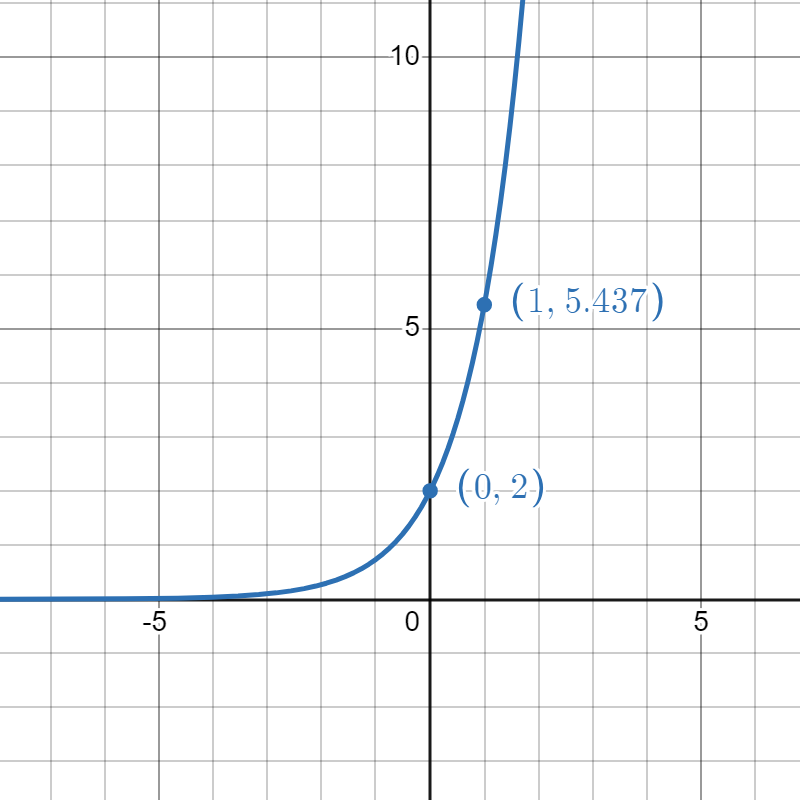
Match the graphs to their functions.
 |
 |
 |
 |
| 1. | 2. | 3. | 4. |
| \( f(x) = 2e^x\) | \(g(x) = 10^x-10 \) | \( h(x) = \left(\frac{1}{2}\right)^x + 1 \) | \( p(x) = -2^x\) |
- Answer
-
- \(h\)
- \(g\)
- \( f\)
- \(p\)
Sketch the graphs of the exponential functions.
- \( f(x) = 10^x\)
- \(f(x) = (0.25)^x \)
- \( f(x) = 2^x \)
- \( f(x) = 2^{x+1} \)
- \( f(x) = -3^x\)
- \( f(x) = -3^x + 1 \)
- Answer
-
1.
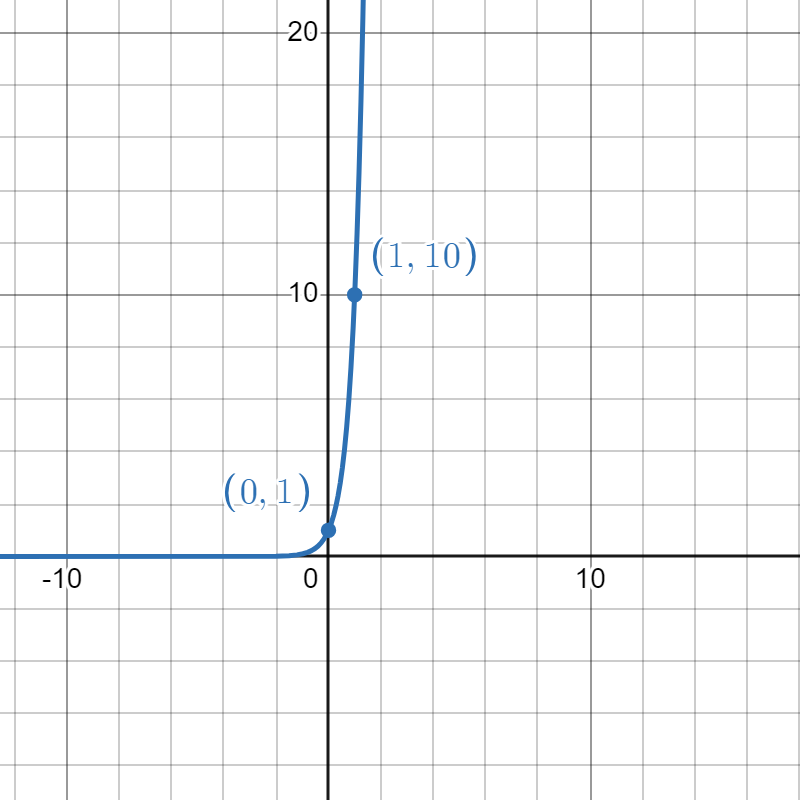
2.

3.

4.

5.
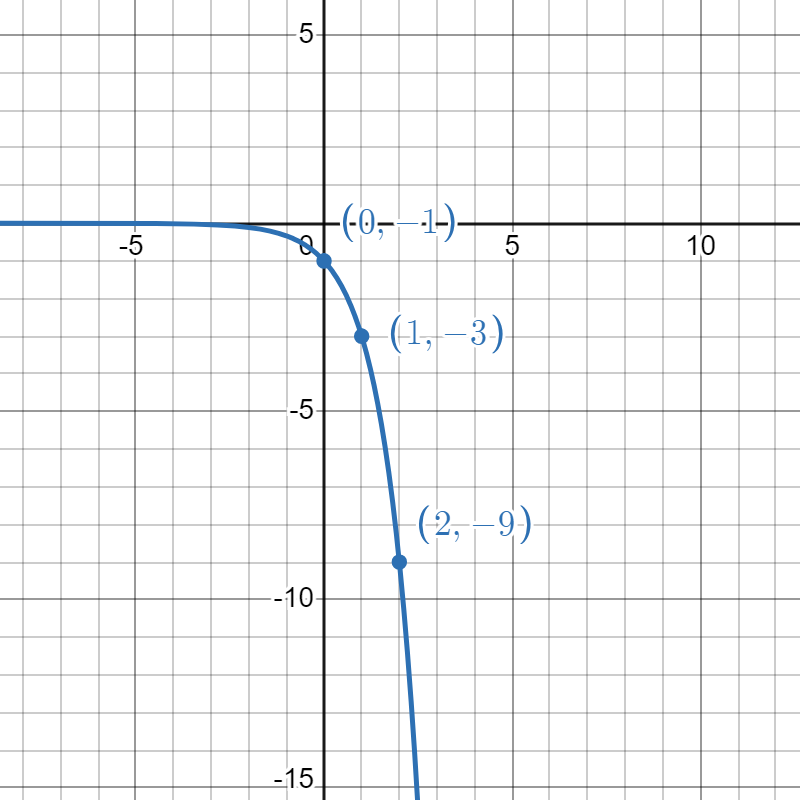
6.

- (Without calculator) Fill in the table of values for the function \( f(x) = 2^x \).
x \( f(x) \) x \( f(x)\) 1 0 2 -1 3 -2 - (Without calculator) Fill in the table of values for the function \( f(x) = \left(\frac{2}{3}\right)^x\).
x \( f(x) \) x \( f(x)\) 1 0 2 -1 3 -2 - (Without calculator) Fill in the table of values for the function \( f(x) = 5^{-x} \).
x \( f(x) \) x \( f(x)\) 1 0 2 -1 3 -2 - For \( f(x) = 5^x \), what should \(x\) be to get \(f(x) = 5\)? What should \(x\) be to get \(f(x) = 25\)?
- For \( f(x) = 5^x\), what should \(x\) be to get \( f(x) = \frac{1}{5} \)? What should \(x\) be to get \( f(x) = 1\)?
- For \(f(x) = 4^x\), what should \(x\) be to get \(f(x) = 2\)?
- For \(f(x) = 8^x\), what should \(x\) be to get \(f(x) = 2\)?
- If \(f(x) = 2^x\) and \(g(x) = 4^x\), is there an \(x\)-value for which \(f(x) = g(x)\)?
- Is there an \(x\)-value such that \( e^x = -2 \)?
- Using technology (calculator or WolframAlpha, for example), fill in the table of values for the function \(f(x) = (1.2)^x \).
x \( f(x) \) x \( f(x) \) -2 0 -1 3.25 -0.5 10
- Answer
-
-
x \( f(x) \) x \( f(x)\) 1 2 0 1 2 4 -1 \( \frac{1}{2}\) 3 8 -2 \( \frac{1}{4} \) -
x \( f(x) \) x \( f(x)\) 1 \( \frac{2}{3} \) 0 1 2 \( \frac{4}{9} \) -1 \( \frac{ 3}{2} \) 3 \( \frac{8}{27} \) -2 \( \frac{9}{4} \) -
x \( f(x) \) x \( f(x)\) 1 \( \frac{1}{5} \) 0 1 2 \( \frac{1}{25} \) -1 5 3 \( \frac{1}{125} \) -2 25 - For \(f(x) = 5\), \(x\) should be 2. For \(f(x) = 25\), \(x \) should be 2.
- For \( f(x) = \frac{1}{5} \), \(x\) should be \(-1\). For \( f(x) = 1\), \(x\) should be 0.
- We want \(x\) such that \( f(x) = 4^x = 2 \). What kind of power should 4 be raised to to get out...its square root? That's right, \(x = \frac{1}{2} \). Check: \( f(1/2) = 4^{\frac{1}{2}} = \sqrt{4} = 2 \).
- Similar reasoning, \(x = \frac{1}{3} \).
- Yes, both pass through \( (0,1)\). Aka, if \(x = 0\), then \(f(x) = g(x) = 1\).
- No, there is no possible input that will make \(f(x) = e^x\) pass below the \(x\)-axis into negative function values.
-
x \( f(x) \) x \( f(x) \) -2 0.694444 0 1 -1 0.833333 3.25 1.80859 -0.5 0.912871 10 6.19174
-

