5.2: Problem or Exercise?
- Last updated
- Jan 16, 2020
- Save as PDF
- Page ID
- 32465
( \newcommand{\kernel}{\mathrm{null}\,}\)
The main activity of mathematics is solving problems. However, what most people experience in most mathematics classrooms is practice exercises. An exercise is different from a problem.
In a problem, you probably don’t know at first how to approach solving it. You don’t know what mathematical ideas might be used in the solution. Part of solving a problem is understanding what is being asked, and knowing what a solution should look like. Problems often involve false starts, making mistakes, and lots of scratch paper!
In an exercise, you are often practicing a skill. You may have seen a teacher demonstrate a technique, or you may have read a worked example in the book. You then practice on very similar assignments, with the goal of mastering that skill.
Note
What is a problem for some people may be an exercise for other people who have more background knowledge! For a young student just learning addition, this might be a problem:
Fill in the blank to make a true statement___+4=7.
But for you, that is an exercise!
Both problems and exercises are important in mathematics learning. But we should never forget that the ultimate goal is to develop more and better skills (through exercises) so that we can solve harder and more interesting problems.
Learning math is a bit like learning to play a sport. You can practice a lot of skills:
- hitting hundreds of forehands in tennis so that you can place them in a particular spot in the court,
- breaking down strokes into the component pieces in swimming so that each part of the stroke is more efficient,
- keeping control of the ball while making quick turns in soccer,
- shooting free throws in basketball,
- catching high fly balls in baseball,
and so on.
But the point of the sport is to play the game. You practice the skills so that you are better at playing the game. In mathematics, solving problems is playing the game!
On Your Own
For each question below, decide if it is a problem or an exercise. (You do not need to solve the problems! Just decide which category it fits for you.) After you have labeled each one, compare your answers with a partner.
- This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers.(Note: Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15. )
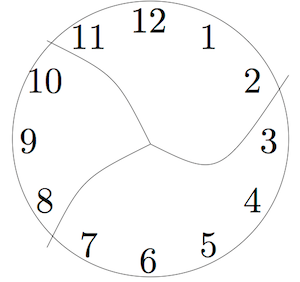
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).
- A soccer coach began the year with a $500 budget. By the end of December, the coach spent $450. How much money in the budget was not spent?
- What is the product of 4,500 and 27?
- Arrange the digits 1–6 into a “difference triangle” where each number in the row below is the difference of the two numbers above it.
- Simplify the following expression: 2+2(53−42)5−222(53−42).
- What is the sum of 52 and 313?
- You have eight coins and a balance scale. The coins look alike, but one of them is a counterfeit. The counterfeit coin is lighter than the others. You may only use the balance scale two times. How can you find the counterfeit coin?

- How many squares, of any possible size, are on a standard 8 × 8 chess board?
- What number is 3 more than half of 20?
- Find the largest eight-digit number made up of the digits 1, 1, 2, 2, 3, 3, 4, and 4 such that the 1’s are separated by one digit, the 2’s are separated by two digits, the 3’s by three digits, and the 4’s by four digits.


