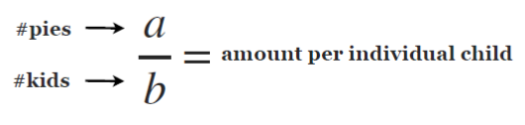One of the things that makes fractions such a difficult concept to teach and to learn is that you have to think about them in a lot of different ways, depending on the problem at hand. For now, we are going to think of a fraction as the answer to a division problem.
Example: Pies per child
Suppose 6 pies are to be shared equally among 3 children. This yields 2 pies per kid. We write \[\frac{6}{3} = 2 \ldotp \nonumber \]

The fraction \(\frac{6}{3}\) is equivalent to the division problem \(6 \div 3 = 2\). It represents the number of pies one whole child receives when three kids share six pies equally.
In the same way …
- Sharing 10 pies among 2 kids yields \(\frac{10}{2} = 5\) pies per kid.
- Sharing 8 pies among 2 children yields \(\frac{8}{2} = 4\) pies per child.
- Sharing 5 pies among 5 kids yields \(\frac{5}{5} = 1\) pie per kid.
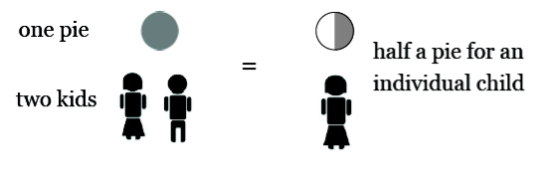
- Sharing 1 pie among 2 children yields \(\frac{1}{2}\), which we call “one-half.”
This final example is actually saying something! It also represents how fractions are usually taught to students:
If one pie is shared equally between two kids, then each child receives a portion of a pie which we choose to call “half.”
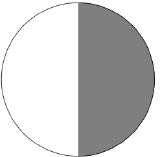
Thus students are taught to associate the number \(`` \frac{1}{2} " \) to the picture  .
.
In the same way, the picture  is said to represent “one-third,” that is, \(\frac{1}{3}\). (And this is indeed the amount of pie an individual child would receive if one pie is shared among three.)
is said to represent “one-third,” that is, \(\frac{1}{3}\). (And this is indeed the amount of pie an individual child would receive if one pie is shared among three.)
The picture  is called “one-fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual receives if three pies are shared among five children.
is called “one-fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual receives if three pies are shared among five children.
And the picture  is called “three-fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared among five children.
is called “three-fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared among five children.
Think / Pair / Share
Carefully explain why this is true: If five kids share three pies equally, each child receives an amount that looks like this:  .
.
Your explanation will probably require both words and pictures.
On Your Own
Work on the following exercises on your own or with a partner.
- Draw a picture associated with the fraction \(\frac{1}{6}\).
- Draw a picture associated with the fraction \(\frac{3}{7}\). Is your picture really the amount of pie an individual would receive if three pies are shared among seven kids? Be very clear on this!
- Let’s work backwards! Here’s the answer to a division problem:
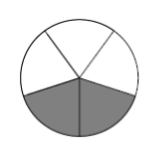
This represents the amount of pie an individual kid receives if some number of pies is shared among some number of children. How many pies? How many children? How can you justify your answers?
- Here’s another answer to a division problem:
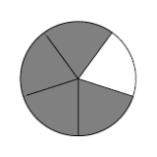
How many pies? How many children? How can you justify your answers?
- Here is another answer to a division problem:
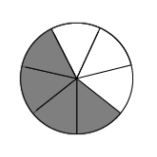
How many pies? How many children? How can you justify your answers?
- Leigh says that “\(\frac{3}{5}\) is three times as big as \(\frac{1}{5}\).” Is this right? Explain your answer.
- Draw a picture for the answer to the division problem \(\frac{4}{8}\). Describe what you notice about the answer.
- Draw a picture for the answer to the division problem \(\frac{2}{10}\). Describe what you notice about the answer.
- What does the division problem \(\frac{1}{1}\) represent? How much pie does an individual child receive?
- What does the division problem \(\frac{5}{1}\) represent? How much pie does an individual child receive?
- What does the division problem \(\frac{5}{5}\) represent? How much pie does an individual child receive?
- Here is the answer to another division problem. This is the amount of pie an individual child receives:

How many pies were in the division problem? How many kids were in the division problem? Justify your answers.
- Here is the answer to another division problem. This is the amount of pie an individual child receives:

How many pies were in the division problem? How many kids were in the division problem? Justify your answers
- Many teachers have young students divide differently shaped pies into fractions. For example, a hexagonal pie is good for illustrating the fractions: $$\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}, \frac{5}{6},\; and\; \frac{6}{6} \ldotp$$
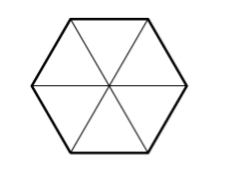
- Why is this shape used? What does \(\frac{1}{6}\) of a pie look like?
- What does \(\frac{6}{6}\) of a pie look like?
- What shape pie would be good for illustrating the fractions \(\frac{1}{8}\) up to \(\frac{8}{8}\)?
Problem 1
Some rectangular pies are distributed to some number of kids. This picture represents the amount of pie an individual child receives. The large rectangle represents one whole pie.

How many pies? How many kids? Carefully justify your answers!
Pies Per Child Model
In our model, a fraction \(\frac{a}{b}\) represents the amount of pie an individual child receives when  pies are shared equally by
pies are shared equally by  kids.
kids.
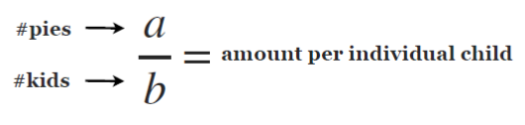
Think / Pair / Share
- What is \(\frac{2}{2}\)? What is \(\frac{7}{7}\)? What is \(\frac{100}{100}\)? How can you use the “Pies Per Child Model” to make sense of \(\frac{a}{a}\) for any positive whole number
 ?
?
- What is \(\frac{2}{1}\)? What is \(\frac{7}{1}\)? What is \(\frac{1876}{1}\)? How can you use the “Pies Per Child Model” to make sense of \(\frac{b}{1}\) for any positive whole number
 ?
?
- Write the answer to this division problem: “I have no pies to share among thirteen kids.” How can you generalize this division problem to make a general statement about fractions?
Definition
For a fraction \(\frac{a}{b}\), the top number  (which, for us, is the number of pies) is called the numerator of the fraction, and the bottom number
(which, for us, is the number of pies) is called the numerator of the fraction, and the bottom number  (the number of kids), is called the denominator of the fraction.
(the number of kids), is called the denominator of the fraction.
Most people insist that the numerator and denominator each be whole numbers, but they do not have to be.
Think / Pair / Share
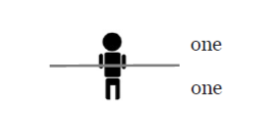
To understand why the numerator and denominator need not be whole numbers, we must first be a little gruesome. Instead of dividing pies, let’s divide kids! Here is one child:

- What would half a kid look like?
- What would one-third of a kid look like?
- What would three-fifths of a child look like?
So, what would $$\frac{1}{\left( \dfrac{1}{2} \right)}$$represent?
This means assigning one pie to each “group” of half a child. So how much would a whole child receive? Well, we would have a picture like this:
The whole child gets two pies, so we have:
\[\frac{1}{\left( \dfrac{1}{2} \right)} = 2 \ldotp \nonumber \]
Jargon: Improper fractions
A fraction with a numerator smaller than its denominator is called (in school math jargon) a proper fraction. For example, \(\frac{45}{58}\) is “proper.”
A fraction with numerator larger than its denominator is called (in school math jargon) an improper fraction. For example, \(\frac{7}{3}\) is “improper.” (In the 1800’s, these fractions were called vulgar fractions.)
For some reason, improper fractions are considered, well, improper by some teachers. So students are often asked to write improper fractions as a combination of a whole number and a proper fraction (often called “mixed numbers”). Despite their name and these prejudices, improper fractions are useful nonetheless!
With a mixed number, you have a good sense of the overall size of the number: “a little more than five,” or “a bit less than 17.” But it is often easier to do calculations with improper fractions (why do you think that is?).
Example: \(\frac{23}{4}\)
If 4 children share 23 pies, we can give them each 5 whole pies. That uses 20 pies, and there are 3 pies left over.
Those three pies are still to be shared equally by the four kids. We have: \[\frac{23}{4} = 5 \frac{3}{4} \ldotp \nonumber \]
Example: \(2 \frac{1}{5}\)
For fun, let us write the number 2 as a fraction with denominator 5: \[2 = \frac{10}{5} \ldotp \nonumber \]
So: \[2 \frac{1}{5} = 2 + \frac{1}{5} = \frac{10}{5} + \frac{1}{5} = \frac{11}{5} \ldotp \nonumber \]
We have written the mixed number \(2 \frac{1}{5}\) as the improper fraction \(\frac{11}{5}\).
Think / Pair / Share
- Write each of the following as a mixed number. Explain how you got your answer. $$\frac{17}{3}, \qquad \frac{8}{5}, \qquad \frac{100}{3}, \qquad \frac{200}{199} \ldotp$$
- Convert each of these mixed numbers into “improper” fractions. Explain how you got your answer. $$3 \frac{1}{4}, \qquad 5 \frac{1}{6}, \qquad 1 \frac{3}{11}, \qquad 200 \frac{1}{200} \ldotp$$
Students are often asked to memorize the names “proper fractions,” “improper fractions,” and “mixed number” so that they can follow directions on tests and problem sets.
But, to a mathematician, these names are not at all important! There is no “correct” way to express an answer (assuming, that the answer is mathematically the right number). We often wish to express our answer in a simpler form, but sometimes the context will tell you what form is “simple” and what form is more complicated.
As you work on problems in this chapter, decide for yourself which type of fraction would be best to work with as you do your task.





 .
. is said to represent “one-third,” that is, \(\frac{1}{3}\). (And this is indeed the amount of pie an individual child would receive if one pie is shared among three.)
is said to represent “one-third,” that is, \(\frac{1}{3}\). (And this is indeed the amount of pie an individual child would receive if one pie is shared among three.) is called “one-fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual receives if three pies are shared among five children.
is called “one-fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual receives if three pies are shared among five children. is called “three-fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared among five children.
is called “three-fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared among five children.