7.3: Funciones de Activación
- Page ID
- 97304
Las funciones de activación se aplican sobre el resultado final de cada perceptrón, permitiendo introducir efectos no lineales al cálculo. Ese es un aspecto fundamental a la hora de trabajar con redes neuronales. Sin estas funciones de activación, una red neuronal del tipo perceptrón multicapa se convertiría en una transformación lineal entre los datos de entrada y de salida, lo que limitaría mucho el tipo de casos que se podrían modelizar con redes neuronales.
La función escalón (binaria) y la función sigmoide fueron las primeras en proponerse y emplearse con éxito, pero se han ido proponiendo muchas otras a lo largo del tiempo. En la actualidad, la función RELU (que pone los número negativos de entrada a cero) es la más empleada.
Hay que tener en cuenta que en muchos casos interesa que sean funciones derivables, dado que se necesita para la optimización de la red. En puntos en lo que esto no sucede (Como RELU en el origen) se suelen usar aproximaciones numéricas para solventarlo.
Merece la pena dedicar un tiempo a analizar las funciones de activación más relevantes en diversos problemas de aprendizaje automático.
Es el tipo de función más sencilla que permite introducir no-linealidad en el modelo sin necesidad de transformaciones complicadas. Es la más usada y la más fácil de entender. Su definición es:
\( f(z) = \begin{cases} z & \text{si } z > 0 \\ 0 & \text{si } z \leq 0 \end{cases} \)
Su representación gráfica es la siguiente:
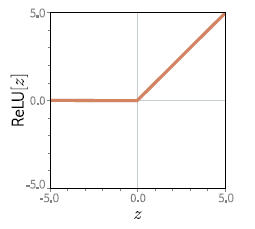
Es útil para realizar clasificaciones binarias (clasificar el input entre solamente dos posibles categorías) y se define como:
\(f(x)=\frac{1}{1+e^{-x}}\)
Su representación gráfica es la siguiente:
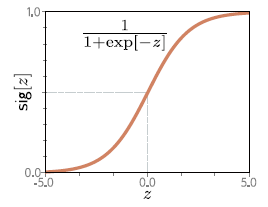
Es fácil ver que la imagen de esta funcion es \(y\in(0,1)\). Esto permite realizar clasificaciones binarias como, por ejemplo: si el output es menor que 0.5 entonces el input pertenece a la primera clase; si el output es mayor que 0.5 pertenece a la segunda clase.
La función softmax es útil para realizar clasificaciones multiclase, en las que se busca clasificar el output entre K categorías diferentes. Esta función toma como input un vector de longitud K (el output de la red neuronal, con sus pesos) y devuelve un vector de la misma longitud K peero ahora con todos los elementos en el intervalo [0,1]. Es una forma de transformar un vector de números reales en una distribución de probabilidad. Dado que los elementos de este vector (el output de sotfmax) se pueden entender como probabilidades, la suma de todos los elementos debe ser uno. Para asegurar la positividad de cada elemento y que la suma de los elementos sea 1, el elemento k-ésimo del output de la función softmax puede definirse como:
\(\text{softmax}_{k}[\textbf{z}]=\frac{e^{z_{k}}}{\sum_{i=1}^{K}e^{z_{i}}}\)

