7.6: Ejemplo- Regresión lineal

La mejor manera de entender el algoritmo de entrenamiento de una red neuronal es mediante un ejemplo sencillo. Empezamos con una tarea sencilla a la par que común dentro del mundo de las ciencias: la regresión lineal. Aproximar un conjunto de datos por una recta es un proceso que todo científico acabará realizando en algún momento, y este proceso puede entenderse como el entrenamiento de una red neuronal.

 

En este caso, nuestra red o modelo toma un input \(x\) y devuelve un output \(y\) que se calcula de forma lineal: \(y=f(x,\phi)=\phi_{o}+\phi_{1}x\). El conjunto de parámetros \(\phi\) determinan una familia de rectas en el plano con distintas pendientes y distintas ordenadas en el origen. Sin embargo, existe una elección óptima de dichos parámetros que es la óptima para ajustar un determinado conjunto de datos \(x,y\).  Se incluye a continuación una serie de rectas en el intervalo [0,5], que solo difieren en los valores de \(\phi\).

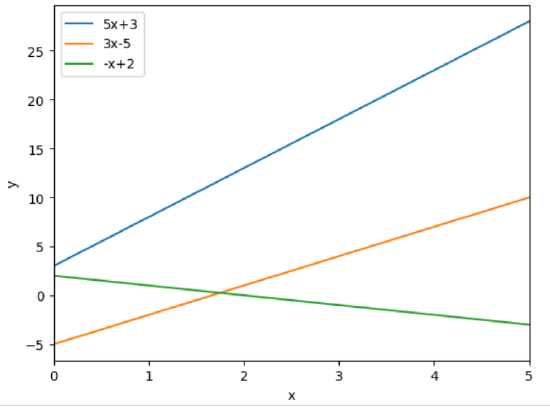
Vayamos al ejemplo concreto. Imaginemos que tenemos un set de datos, queremos encontrar la recta que mejor se ajusta a nuestros datos. Aquí entra el primer problema: ¿qué es ajustarse bien? En este caso puede parecer sencillo, pero en situaciones más complejas, ajustarse bien puede ser una definición complicada. Esta pregunta es equivalente a una pregunta ya tratada en otra sección: ¿qué función de pérdida debo elegir? En este caso, dado que estamos tratando con puntos en el plano y queremos minimizar su distancia a una recta; podemos definir como función de pérdida dicha distancia geométrica entre puntos. Por tanto, el error cuadrático medio o el error absoluto medio podrían ser buenos candidatos, pues ambos cuantifican la distancia geométrica entre los puntos de nuestra recta y los de nuestro set. Convencionalmente se usa el error cuadrático medio, ajuste que se denomina ajuste de mínimos cuadrados. Este nombre viene dado por la elección de función de pérdida, que en este caso tendría la forma:

\[ L[\phi]=\sum_{i=1}^{N}(f(x_{i},\phi)-y_{i})^2=\sum_{i=1}^{N}(\phi_{o}+\phi_{1}x_{i}-y_{i})^2 \]

Podría haberse elegido como función de pérdida simplemente la suma del valor absoluto de la desviación (sin elevarse al cuadrado), pero convencionalmente se eleva al cuadrado para que las desviaciones mayores sumen aún más; de esta forma haciendo que mayores desviaciones hagan crecer mucho la pérdida. Veamos un ejemplo. Puede verse claramente que la recta que mejor se ajusta es aquella con menor pérdida.

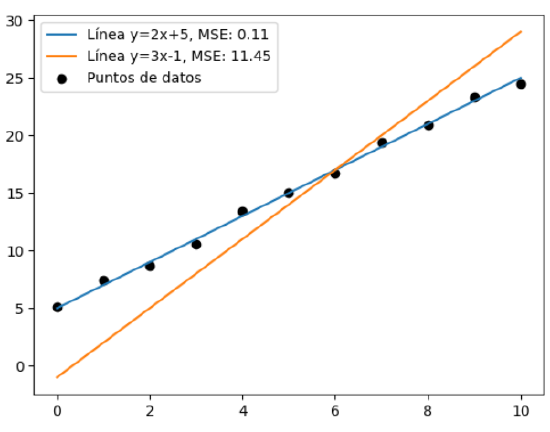
Una vez fijados los puntos, la pérdida es una función de únicamente \(\phi_{o}\) y \(\phi_{1}\). Veamos una representación de esta función bidimensional, con sus correspondientes curvas de nivel, usando unos valores de \(\phi_{o}\in[1,3]\) y \(\phi_{1}\in[4,6]\).

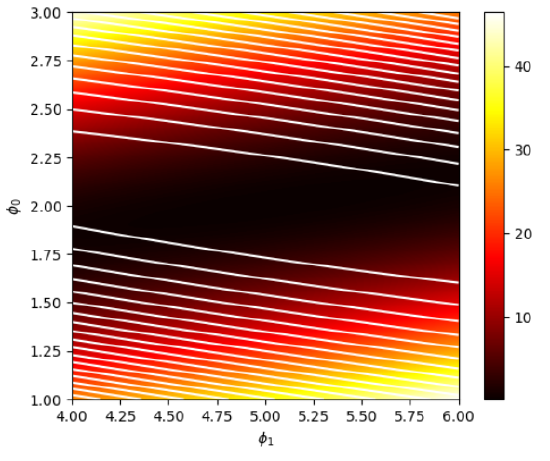
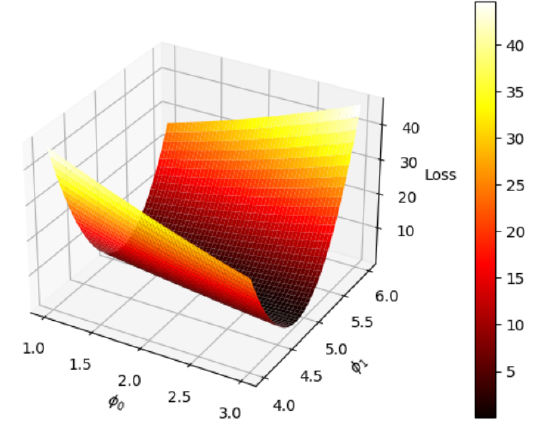
Para obtener este mapa simplemente hay que evaluar la pérdida para todas las posibles combinaciones de \(\phi_{o}\) y \(\phi_{1}\). Podemos ver que los valores menores de la pérdida se encuentran alrededor de \(\phi_{o}\approx 2\) y \(\phi_{1} \approx 5\), como predecíamos. El valor óptimo de los parámetros de la red se encuentra en la región coloreada en negro. Nuestro objetivo será acercanos al máximo global de la función todo lo posible. Para ello usaremos el método del gradiente descendiente estocástico (esto último para asegurar la convergencia). Lo primero que necesitaremos será el gradiente de la pérdida, para poder posteriormente trabajar con él y minimizar la pérdida. En nuestro caso el gradiente puede ser calculado de forma analítica:

\[ \vec{\nabla L}=\frac{\partial L}{\partial \phi}=\frac{\partial}{\partial \phi}\sum_{i=1}^{N}l_{i}=\sum_{i=1}^{N}\frac{\partial l_{i}}{\partial \phi}\]

\(L\) es la pérdida total, \(l_{i}\) es la pérdida correspondiente a cada punto del set usado para entrenar. El gradiente de la pérdida para cada punto puede calcularse también:

\[ \frac{\partial l_{i}}{\partial \phi}=\begin{pmatrix} \frac{\partial l_{i}}{\partial \phi_{o}} \\ \frac{\partial l_{i}}{\partial \phi_{1}}   \end{pmatrix} = \begin{pmatrix} 2(\phi_{o}+\phi_{1}x_{i}-y_{i})  \\ 2x_{i}(\phi_{o}+\phi_{1}x_{i}-y_{i}) \end{pmatrix} \]

Ya solamente queda implementar el método del gradiente descendiente (ignoraremos la parte estocástica de momento). La regla de actualización de los parámetros en cada iteración será:

\[ \phi_{t}=\phi_{t-1}-\epsilon \frac{\partial L}{\partial \phi} \]

Por componentes, esta ecuación puede escribirse como:

\[ \phi_{o,t} = \phi_{o,t-1} - 2\epsilon \sum_{i=1}^{N}(\phi_{o,t-1}+\phi_{1,t-1}x_{i}-y_{i}) \]

\[ \phi_{1,t} = \phi_{1,t-1} - 2\epsilon \sum_{i=1}^{N}x_{i}(\phi_{o,t-1}+\phi_{1,t-1}x_{i}-y_{i}) \]

Si se eligen unos valores iniciales de ambos parámetros, puede procederse al cálculo iterativo del mínimo de la pérdida. Debe elegirse de forma sensata la tasa de aprendizaje \(\epsilon\) para que las iteraciones no se desvíen demasiado del mínimo. Sin embargo, para asegurar la convergencia, se usará tan solo un pequeño subset de los datos disponibles en cada iteración, elegidos de forma aleatoria (gradiente descendiente estocástico). Usando tan solo 30 iteraciones y una tasa de aprendizaje de 0.002, pudo obtenerse el siguiente ajuste:

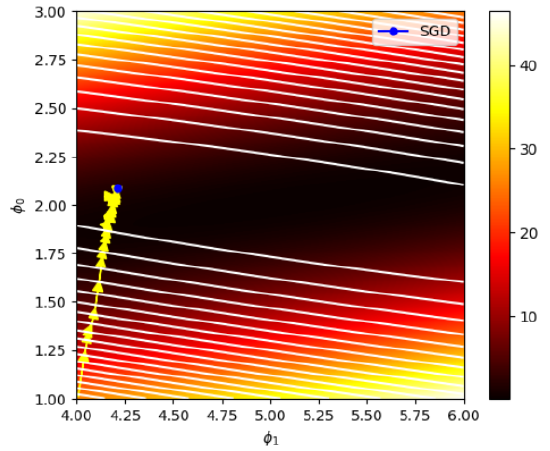
Podemos ver que, a medida que el método va progresando, se va acercando a la zona de menor pérdida. Los valores finales que se han obtenido son \(\phi_{o}\approx 2.01\) y  \(\phi_{1}\approx 4.21\); que entran dentro del rango de lo esperado (aunque podría llegarse a un valor más preciso usando otro optimizador, tasa de aprendizaje o número de iteraciones). El modelo ha sido entrenado satisfactoriamente y ahora podría usarse para predecir el output esperado \(y\) dado un input \(x\) usando los parámetros calculados.