8.1: Redes neuronales superficiales

Last updated
Save as PDF

Page ID: 149400

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Las redes neuronales superficiales son aquellas redes neuronales con una sola capa oculta. Una red neuronal superficial tan solo tiene 3 capas:la capa de entrada, la capa oculta (donde se encuentran los pesos y se realiza el entrenamiento) y una capa de salida. Empezaremos viendo un ejemplo para un caso particular y posteriormente generalizaremos el resultado. Imaginemos una red neuronal con 10 parámetros, de forma que tome un input $x$ y devuelva un output:

\[ y=\phi_{0}+\phi_{1}a(\theta_{10}+\theta_{11}x)+\phi_{2}a(\theta_{20}+\theta_{21}x)+\phi_{3}a(\theta_{30}+\theta_{31}x) \]

$a(x)$ es la función de activación que elijamos, nosotros para este ejemplo usaremos ReLU. La combinación de diversos parámetros en la ecuación anterior determina una familia de funciones, veamos un ejemplo:

$clipboard_e18320ff0873e04cd15242447c98c032c.png$

Fuente: Understanding Deep Learning, Simon JD Prince

El cambio en los parámetros puede cambiar la altura de cada región, la posición de los vértices o las pendientes de cada recta.

El funcionamiento de la red neuronal puede reescribirse y reestructurarse en función de tres unidades ocultas que son independientes entre sí. Definimos:

\[ h_{1}=a(\theta_{10}+\theta_{11}x) \]

\[ h_{2}=a(\theta_{20}+\theta_{21}x) \]

\[ h_{3}=a(\theta_{30}+\theta_{31}x) \]

Cada $h_{i}$ se denomina unidad oculta. La combinación lineal de las 3 unidades ocultas (más un bias) nos da el efecto de la red neuronal:

\[ y=\phi_{0}+\phi_{1}h_{1}+\phi_{2}h_{2}+\phi_{3}h_{3} \]

Cada unidad oculta toma una función lineal y posteriormente la pasa por una función de activación; luego los outputs de cada unidad oculta son sumados con un cierto peso y se añade un bias $\phi_{0}$ que controla la altura de la función. Veamos el ejemplo con el desglose de cada unidad oculta, y posteriormente su suma:

$clipboard_eb878d17648cfbd70a8f65b1ed1d3db2c.png$

La primera fila muestra las funciones lineales (vemos tres rectas normales); la segunda fila muestra las rectas pasadas por el ReLU (solo nos quedamos con la parte positiva) y la tercera fila muestra las rectas pasadas por el ReLU ponderadas con un cierto $\phi_{i}$ que modifica la pendiente del tramo que no es cero. Por último, se muestra la suma de la tercera fila. Podemos ver que los 3 puntos donde cada unidad oculta se hace cero representan los vértices de la función final. Al haber 3 unidades ocultas, la función tendrá 3 vértices y por tanto podrá dividirse en 3+1=4 zonas. En general, si hay N unidades ocultas, la gráfica final tendrá N vértices y podrá dividirse en N+1 zonas. Fijémonos ahora en la zona gris de la última figura. Podemos ver que solamente están contribuyendo al modelo final las unidades $h_{1}$ y $h_{3}$, decimos que estas unidades están activas, mientras que la unidad $h_{2}$ no está contribuyendo porque el ReLU la ha hecho cero, decimos que está inactiva. La pendiente de la recta en esta zona gris es la combinación lineal de las pendientes de las unidades activas, pesadas con los $\phi_{i}$: $\phi_{1}\theta_{11}+\phi_{3}\theta_{31}$. Cada zona se denomina región lineal.

La arquitectura de esta red puede resumirse en la siguiente figura:

$clipboard_eca2cff68a00acddbcb3c7d98cdbab4e6.png$ La figura de la izquierda muestra de forma explícita todos los parámetros que se están utilizando (mediante cajas naranjas que representa la incorporación de estos parámetros como otra unidad), así como la jerarquía de las unidades ocultas y su posterior combinación. En la práctica resulta más conveniente usar esquemas como el de la segunda figura, puesto que el número de parámetros suele ser muy alto y esta representación resulta más sencilla e intuitiva.

Una vez entendido este sencillo ejemplo de red con 3 unidades ocultas, es necesario introducir un teorema que justifique el uso de estas funciones ReLU y que solamente usemos rectas.

Teorema: Teorema de Aproximación Universal

Toda función continua que mapea intervalos de números reales a algún intervalo de salida de números reales puede ser aproximado por una red neuronal superficial (una sola capa oculta) a cualquier precisión deseada.

Este teorema puede resultar chocante pero es en realidad un resultado bastante intuitivo, y la mejor forma de verlo es mediante un ejemplo. Se muestra a continuación una función arbitraria y la aproximación mediante una red neuronal superficial (funciones lineales definidas a trozos) con 5, 10 y 15 regiones lineales (es decir, usando 4,9 y 14 unidades ocultas):

$clipboard_eb8086b02e38fc8eca335c63b6340aef1.png$ ç

Vemos que la aproximación a la función arbitraria es mejor cuanto mayor es el número de regiones lineales. De esta forma, podría alcanzarse cualquier precisión en la aproximación simplemente añadiendo más unidades ocultas.

Veamos ahora que una red neuronal superficial también puede tener más de un output, y los efectos que tiene esto. Se incluye a continuación el funcionamiento y arquitectura de la red:

$clipboard_e3f7168e38372c7c569a57752e8dd1bea.png$ $ h_{1}=a[\theta_{10}+\theta_{11}x] $ $ h_{2}=a[\theta_{20}+\theta_{21}x] $

$ h_{3}=a[\theta_{30}+\theta_{31}x] $ $ h_{4}=a[\theta_{40}+\theta_{41}x] $

$y_{1}=\phi_{10}+\phi_{11}h_{1}+\phi_{12}h_{2}+\phi_{13}h_{3}+\phi_{14}h_{4} $

$y_{2}=\phi_{20}+\phi_{21}h_{1}+\phi_{22}h_{2}+\phi_{23}h_{3}+\phi_{24}h_{4} $

18 parámetros

$clipboard_e2b01683c5eadf7ae63a24a5c03637596.png$ Vemos ahora que, al tener 4 unidades ocultas, tenemos 4 vértices y 5 regiones lineales. Cada output tiene su propio comportamiento y pendiente, pero ambas comparten los mismos vértices porque ambas son la combinación lineal de las mismas unidades ocultas: el ReLU ha generado un vértice en el mismo punto para ambas.ç

Hemos podido comprobar que la dimensión del output NO modifica el número de regiones disponibles, que sigue siendo función solo del número de unidades ocultas.

Comprobaremos ahora que este NO es el caso cuando modificamos las dimensiones del input. Supongamos ahora una red con la siguiente arquitectura:

$clipboard_e8941c527c0222fab820d57a948ccdfd6.png$ $h_{i}=a[\theta_{i0}+\theta_{i1}x_{1}+\theta_{i2}x_{2} $

El input de la función de activación ya no es una recta, sino un plano. Al pasarlo por la función de activación, se mapean a cero aquellos valores de z negativos, definiendo z como $z=theta_{i0}+\theta_{i1}x_{1}+\theta_{i2}x_{2}$.

ReLU ya no genera vértices entre regiones lineales sino entre regiones poligonales.

Como siempre, tratemos de visualizar esto mediante un ejemplo. Se muestra a continuación el desglose de esta red neuronal superficial:

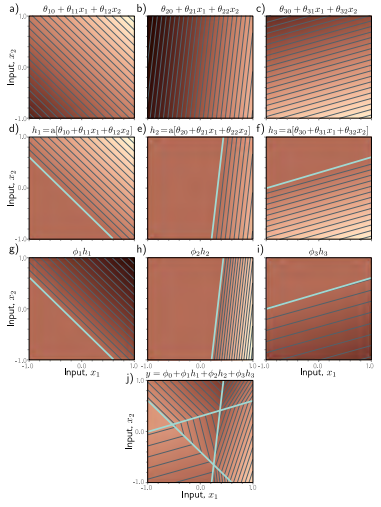
$clipboard_e7bef9f6b222fa0e230ff57a6394b4b20.png$

La primera fila representa los planos correspondientes a cada unidad oculta. La segunda fila representa los planos mapeados, con las zonas negativas mapeadas a 0 por el ReLU. La tercera fila representa el plano mapeado pesado con su correspondiente $\phi_{i}$. Por último, la última imagen representa la combinación lineal de la tercera, es una superficie lineal continua que consiste de regiones poligonales convexas. Cada región tiene unas unidades activas u otras. En este caso hemos pasado de regiones 2D (1 dimensión output 1 dimensión input) a regiones 3D (2 dimensiones input 1 dimensión output).

Obviamente, si seguimos aumentando el número de dimensiones output, pasaremos a representaciones en más dimensiones que ya no podemos visualizar. Para el caso de tener el mismo número de unidades ocultas $D$ y dimensiones del input $D_{i}$, podríamos alinear cada hiperplano con uno de los ejes. Para dos dimensiones de input podemos dividir el espacio en cuatro cuadrantes; para tres dimensiones de input podemos dividir el espacio en ocho octantes... para $D_{i}$ dimensiones se crean \/2^{D_{i}} \) ortantes. Es común que las redes neuronales tengan más unidades ocultas que dimensiones del input, así que crean más de $2^{D_{i}}$ regiones lineales. Se incluye a continuación una representación del número de regiones del espacio input-output para distinto número de unidades ocultas y de dimensiones del input. Podemos ver que crece muy rápidamente, teniendo D=500 unidades ocultas y $D_{i}=100$ dimensiones del input, podemos tener $10^{107}$ regiones lineales.

$clipboard_edee23d7929f7832057ee92d99408a05b.png$

Pasemos ahora al caso general para una red neuronal superficial que toma inputs $x\in\mathbb{R}^{D_{i}}$ y da outputs $y\in\mathbb{R}^{D_{o}}$ usando $h\in\mathbb{R}^{D}$. Cada unidad oculta funciona como:

\[ h_{d}=a\left[ \theta_{d0}+\sum_{i=1}^{D_{i}}\theta_{di}x_{i} \right] \]

Estas unidades se combinan linealmente para crear el output:

\[ y_{j}=\phi_{j0}+\sum_{d=1}^{D}\phi_{jd}h_{d} \]

Search

Text Color

Text Size

Margin Size

Font Type