Macdonald Polynomials and Demazure Characters
- Page ID
- 1060
Introduction
We will here discuss the connection between nonsymmetric Macdonald polynomials and the characters of Demazure modules for \(\widehat{\mathfrak{sl}}(n)\) as given in [3]. We assume a familiarity with affine (untwisted) Lie algebras, specifically \(\widehat{\mathfrak{sl}}(n)\), but will give all necessary facts about Demazure modules and nonsymmetric Macdonald polynomials here.
Nonsymmetric Macdonald Polynomials
Recall that nonsymmetric Macdonald polynomials \(E_\lambda(z_1, \dots z_n,q,t)\) are indexed by compositions \(\lambda \in \mathbb{N}^n\) and that they form a basis of \(\mathbb{C}(q,t)[z_1, \dots, z_n]\). Henceforth we specialize to \(t = 0\), and write
\[E_\lambda = E_\lambda(z_1, \dots, z_n, q,0)\].
We can generate these polynomials recursively via the endomorphisms \(\Phi, H_0, H_1, \dots, H_{n-1}\) acting on the space \(\mathbb{Z}[q,q^{-1}][z_1, \dots, z_n]\) (note that when we specialize to \(t = 0\) we drop from the space \(\mathbb{C}(q,t)[z_1, \dots, z_n]\) to \(\mathbb{Z}[q,q^{-1}][z_1, \dots, z_n]\)). \(\Phi, H_1, \dots, H_{n-1}\), are defined such that
\[\bar{H_i} = s_i - z_{i+1}{1 - s_i \over z_i - z_{i+1}}\;\;\;\;\;\;\;\;\;\;\;\; 1 \leq i \leq n-1\]
\[\Phi f(z_1, \dots, z_n) = z_n f^{-1}(q^{-1}z_n,z_1, \dots, z_{n-1})\]
There is an \(\bar{H}_0\) too but we will not discuss it. The recursive rules tell us that after setting \(E_{(0^n)} = 1\), then
\[q^{\lambda_1}\Phi E_{(\lambda_1, \dots, \lambda_n)} = E_{(\lambda_2, \dots, \lambda_n, \lambda_1 + 1)}\]
\[q^{\lambda_1 - \lambda_n + 1}\bar{H_0}E_\lambda = E_{(\lambda_n -1, \lambda_2, \dots, \lambda_{n-1}, \lambda_1 +1)} \;\;\;\;\;\;\;\; \text{if } \lambda_1 > \lambda_n - 1\]
and otherwise \(q^{\lambda_1 - \lambda_n +1}\bar{H_0}E_\lambda = E_\lambda \). Finally,
\[\bar{H_i}E_\lambda = E_{s_i \lambda} \;\;\;\;\;\;\;\;\; \text{if } \lambda_i < \lambda_{i+1}\]
and otherwise \(\bar{H_i}E_\lambda = E_\lambda \). These operators should be reminiscent of the action of the Weyl group of \(\widehat{\mathfrak{sl}}(n)\) on compositions.
As an example suppose that for \(n = 3\) we want to generate \(E_{(1,2,1)}\). Then we could apply the composition \(\bar{H_2} \Phi^4\) to \(E_{(0,0,0)}\) to get
\[\Phi(E_{(0,0,0)}) = E_{(0,0,1)} = z_3, \]
\[\Phi(E_{(0,0,1)}) = E_{(0,1,1)} = z_2z_3, \]
\[\Phi(E_{(0,1,1)}) = E_{(1,1,1)} = z_1z_2z_3, \]
\[\Phi(E_{(1,1,1)}) = E_{(1,1,2)} = z_1z_2z_3^2, \]
\[\bar{H_2}(E_{(1,1,2)}) = E_{(1,2,1)} = z_1z_2^2z_3 + z_1z_2z_3^2 \]
Demazure Modules
In this section we let \( \mathfrak{g} \) be a Kac-Moody algebra associated with Cartan datum \((\mathfrak{h},\Pi,\Pi^\vee, P, P^\vee) \). We closely follow chapter 2 of [1]. Recall that a \( \mathfrak{g} \)-module \(V\) is a weight module if it admits a weight space decomposition:
\[V = \bigoplus_{\mu \in \mathfrak{h}^*} V_\mu \]
where
\[V_\mu = \{ v \in V \; | \; hv = \mu(h)v \;\; \text{for all} \;\; h \in \mathfrak{h}\; \}\]
A vector \(v \in V_\mu\) is called a weight vector of weight \(\mu\) if \(e_i v = 0\) for all \(i \in I\), \(v\) is called a maximal weight vector. The dimension \(\dim V_\mu\) is called the weight multiplicity of \(\mu\). When \(\dim V_\mu < \infty \) for all \(\mu\), the
character of \(V\) is defined to be
\[\text{ch}V = \sum_\mu \dim V_\mu e^\mu \]
where \(e^\mu\) are formal basis elements of the group algebra \(\mathbb{F}[\mathfrak{h}^*]\) with multiplication \(e^\lambda e^\mu = e^{\lambda + \mu}\). We call a \(\mathfrak{g}\)-module \(V\) a highest weight module of highest weight \(\lambda \in \mathfrak{h}^*\) if there exists a nonzero vector \(v_\lambda \in V\) such that
\[e_iv_\lambda = 0 \;\;\;\; \text{for all } i \in I,\]
\[h v_\lambda = \lambda(h)v \;\;\;\; \text{for all } h \in \mathfrak{h},\]
\[ V = U(\mathfrak{g})v_\lambda \;\;\;\; (\text{ or } U^-v_\lambda = V \; ),\]
where we here use the decomposition \(U(\mathfrak{g}) \cong U^- \otimes U^0 \otimes U^{+}\) of the universal enveloping algebra of \(\mathfrak{g}\). An element \( \Lambda \in \mathfrak{h}^* \) is a dominant integral weight if \(\Lambda \) belongs to the set,
\[ P^+ = \{ \; \Lambda \in P \; | \; \lambda(h_i) \in \mathbb{Z}_{\geq 0} \;\; \text{for all } i \in I\}\]
The irreducible highest weight \(\mathfrak{g} \)-modules \(V(\Lambda)\) where \(\Lambda\) is a dominant integral weight have the special property that the Chevalley generaters \(e_i \) and \(f_i\) are locally nilpotent on \(V(\Lambda)\). This allows us to construct a well-defined automorphism
\[\tau_i = (\exp f_i)(\exp (-e_i))(\exp f_i)\]
where the action of \(\tau_i\) on weight spaces is given by
\[ \tau_i V_\lambda = V_{s_i \lambda} \;\;\;\;\;\;\; \text{for all } i \in I, \; \lambda \in \text{wt}(V)\]
here \(s_i\) denotes the generator of the Weyl group associated with \( \mathfrak{g} \) with index \( i\).
If we still assume that \(\Lambda \) is a dominant integral weight, \(V = V(\Lambda)\) the unique irreducible highest weight \( \widehat{\mathfrak{sl}}(n)\)-module with highest weight \(\Lambda \), then the weight space \( V_{w(\Lambda)} \) of weight \( w(\Lambda) \) generates a \( U^+(\widehat{\mathfrak{sl}}(n)\)-module, \(E_w(\Lambda)\) which is called a Demazure module. Note that Demazure modules are finite dimensional, and also that they form a filtration on \(V(\Lambda)\) which is compatible with the Bruhat order on \(W\):
\[ w \leq w' \;\;\;\; \implies \;\;\;\; E_w(\Lambda) \subseteq E_{w'}(\Lambda) \]
We can also define Demazure operators that act on the group ring of the weight lattice \( P \):
\[ \Delta_i = {1 - e^{-\alpha_i}s_i \over 1 - e^{-\alpha_i}} \]
where \(s_i\) is the simple reflection in the Weyl group with respect to simple root \( \alpha_i\). To \( w \in W \) with reduced decomposition \( w = s_{i_1} s_{i_2} \dots s_{i_j} \) we can then associate the Demazure operator
\[\Delta_{w} = \Delta_{i_1} \Delta_{i_2} \dots \Delta_{i_j} \],
There is a nice connection between characters and Demazure operators given by the formula [2]:
\[\chi(E_w(\Lambda)) = \Delta_w(e^\Lambda). \]
The Connection
We let \(\Lambda_0, \Lambda_1, \dots, \Lambda_{n-1} \) be the \( n\)-fundamental weights of \( \widehat{\mathfrak{sl}}(n)\). Recall that these \( \Lambda_i \) are defined such that \((\Lambda_i, \alpha_j) = \delta_{ij}\). Finally,
\[ \delta = \sum^{n-1}_{i = 0} \alpha_i. \]
For the connection between \( E_\lambda \) and characters of Demazure modules we want to relate the action of \( \bar{H_i} \) and \( \Phi \) to operators on \( P \). More specifically, we would like a commutative diagram

We can get this by defining \( \pi: \mathbb{Z}[q,q^{-1}][z_1, \dots, z_n] \rightarrow P\) on generators by
\[ \pi(z_i) = e^{\Lambda_{i-1} - \Lambda_i}, \;\;\;\;\; \pi(z_n) = e^{\Lambda_{n-1} - \Lambda_0}, \;\;\;\;\; \pi(q) = e^{-\delta}. \]
(note that this definition is slightly different to that found in the paper). We get a similar commutative diagram for \( \Phi \):
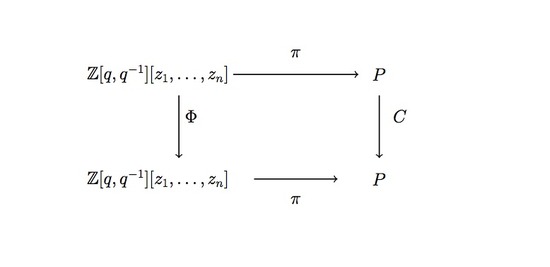
The main result of [3] is then that through the homomorphism \( \pi \), we can identify
\[ q^{-u(\lambda) + u(\eta_{\lambda})} E_\lambda \;\;\;\;\;\;\; \text{with} \;\;\;\;\;\;\; \chi(E_w(\Lambda_i))\]
where \(u(\lambda)\) and \(\eta_{\lambda}\) (this is a partition) depend only on \(\lambda\) and \(i = |\lambda| \text{mod}\; n\) and where \(w\) is an specific affine Weyl group element defined such that \(w\) acts on \(\eta_{|\lambda|}\) to give \(\lambda\).
References
- J. Hong and S.J. Kang. Introduction to quantum groups and crystal bases, volume 42 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 2002.
- S. Kumar, Demazure character formula in arbitrary Kac-Moody setting, Invent. Math. 89 (1987), 395-423.
- Y. Sanderson, On the connection between Macdonald polynomials and Demazure characters, J. Algebraic Combin. 11 (2000), no.3, 269-275.

