Macdonald Polynomials and Demazure Characters

Introduction

We will here discuss the connection between nonsymmetric Macdonald polynomials and the characters of Demazure modules for \(\widehat{\mathfrak{sl}}(n)\) as given in [3]. We assume a familiarity with affine (untwisted) Lie algebras, specifically \(\widehat{\mathfrak{sl}}(n)\), but will give all necessary facts about Demazure modules and nonsymmetric Macdonald polynomials here.

Nonsymmetric Macdonald Polynomials

Recall that nonsymmetric Macdonald polynomials \(E_\lambda(z_1, \dots z_n,q,t)\) are indexed by compositions \(\lambda \in \mathbb{N}^n\) and that they form a basis of \(\mathbb{C}(q,t)[z_1, \dots, z_n]\). Henceforth we specialize to \(t = 0\), and write

\[E_\lambda = E_\lambda(z_1, \dots, z_n, q,0)\].

We can generate these polynomials recursively via the endomorphisms \(\Phi, H_0, H_1, \dots, H_{n-1}\) acting on the space \(\mathbb{Z}[q,q^{-1}][z_1, \dots, z_n]\) (note that when we specialize to \(t = 0\) we drop from the space \(\mathbb{C}(q,t)[z_1, \dots, z_n]\) to \(\mathbb{Z}[q,q^{-1}][z_1, \dots, z_n]\)). \(\Phi, H_1, \dots, H_{n-1}\), are defined such that

\[\bar{H_i} = s_i - z_{i+1}{1 - s_i \over z_i - z_{i+1}}\;\;\;\;\;\;\;\;\;\;\;\; 1 \leq i \leq n-1\]

\[\Phi f(z_1, \dots, z_n) = z_n f^{-1}(q^{-1}z_n,z_1, \dots, z_{n-1})\]

There is an \(\bar{H}_0\) too but we will not discuss it. The recursive rules tell us that after setting \(E_{(0^n)} = 1\), then

\[q^{\lambda_1}\Phi E_{(\lambda_1, \dots, \lambda_n)} = E_{(\lambda_2, \dots, \lambda_n, \lambda_1 + 1)}\]

\[q^{\lambda_1 - \lambda_n + 1}\bar{H_0}E_\lambda = E_{(\lambda_n -1, \lambda_2, \dots, \lambda_{n-1}, \lambda_1 +1)} \;\;\;\;\;\;\;\; \text{if } \lambda_1 > \lambda_n - 1\]

and otherwise \(q^{\lambda_1 - \lambda_n +1}\bar{H_0}E_\lambda = E_\lambda \). Finally,

\[\bar{H_i}E_\lambda = E_{s_i \lambda} \;\;\;\;\;\;\;\;\; \text{if } \lambda_i < \lambda_{i+1}\]

and otherwise \(\bar{H_i}E_\lambda = E_\lambda \). These operators should be reminiscent of the action of the Weyl group of \(\widehat{\mathfrak{sl}}(n)\) on compositions.

As an example suppose that for \(n = 3\) we want to generate \(E_{(1,2,1)}\). Then we could apply the composition \(\bar{H_2} \Phi^4\) to \(E_{(0,0,0)}\) to get

\[\Phi(E_{(0,0,0)}) = E_{(0,0,1)} = z_3, \]

\[\Phi(E_{(0,0,1)}) = E_{(0,1,1)} = z_2z_3, \]

\[\Phi(E_{(0,1,1)}) = E_{(1,1,1)} = z_1z_2z_3, \]

\[\Phi(E_{(1,1,1)}) = E_{(1,1,2)} = z_1z_2z_3^2, \]

\[\bar{H_2}(E_{(1,1,2)}) = E_{(1,2,1)} = z_1z_2^2z_3 + z_1z_2z_3^2 \]

Demazure Modules

In this section we let \( \mathfrak{g} \) be a Kac-Moody algebra associated with Cartan datum \((\mathfrak{h},\Pi,\Pi^\vee, P, P^\vee) \). We closely follow chapter 2 of [1]. Recall that a \( \mathfrak{g} \)​-module \(V\) is a weight module if it admits a weight space decomposition:

\[V = \bigoplus_{\mu \in \mathfrak{h}^*} V_\mu \]

where

\[V_\mu = \{ v \in V \; | \; hv = \mu(h)v \;\; \text{for all} \;\; h \in \mathfrak{h}\; \}\]

A vector \(v \in V_\mu\) is called a weight vector of weight \(\mu\) if \(e_i v = 0\) for all \(i \in I\), \(v\) is called a maximal weight vector. The dimension \(\dim V_\mu\) is called the weight multiplicity of \(\mu\). When \(\dim V_\mu < \infty \) for all \(\mu\), the

character of \(V\) is defined to be

\[\text{ch}V = \sum_\mu \dim V_\mu e^\mu \]

where \(e^\mu\) are formal basis elements of the group algebra \(\mathbb{F}[\mathfrak{h}^*]\) with multiplication \(e^\lambda e^\mu = e^{\lambda + \mu}\). We call a \(\mathfrak{g}\)-module \(V\) a highest weight module of highest weight \(\lambda \in \mathfrak{h}^*\) if there exists a nonzero vector \(v_\lambda \in V\) such that

\[e_iv_\lambda = 0 \;\;\;\; \text{for all } i \in I,\]

\[h v_\lambda = \lambda(h)v \;\;\;\; \text{for all } h \in \mathfrak{h},\]

\[ V = U(\mathfrak{g})v_\lambda \;\;\;\; (\text{ or } U^-v_\lambda = V \; ),\]

where we here use the decomposition \(U(\mathfrak{g}) \cong U^- \otimes U^0 \otimes U^{+}\) of the universal enveloping algebra of \(\mathfrak{g}\). An element \( \Lambda \in \mathfrak{h}^* \) is a dominant integral weight if \(\Lambda \) belongs to the set,

\[ P^+ = \{ \; \Lambda \in P \; | \; \lambda(h_i) \in \mathbb{Z}_{\geq 0} \;\; \text{for all } i \in I\}\]

The irreducible highest weight \(\mathfrak{g} \)-modules \(V(\Lambda)\) where \(\Lambda\) is a dominant integral weight have the special property that the Chevalley generaters \(e_i \) and \(f_i\) are locally nilpotent on \(V(\Lambda)\). This allows us to construct a well-defined automorphism

\[\tau_i = (\exp f_i)(\exp (-e_i))(\exp f_i)\]

where the action of \(\tau_i\) on weight spaces is given by

\[ \tau_i V_\lambda = V_{s_i \lambda} \;\;\;\;\;\;\; \text{for all } i \in I, \; \lambda \in \text{wt}(V)\]

here \(s_i\) denotes the generator of the Weyl group associated with \( \mathfrak{g} \) with index \( i\).

If we still assume that \(\Lambda \) is a dominant integral weight, \(V = V(\Lambda)\) the unique irreducible highest weight \( \widehat{\mathfrak{sl}}(n)\)-module with highest weight \(\Lambda \), then the weight space \( V_{w(\Lambda)} \) of weight \( w(\Lambda) \) generates a \( U^+(\widehat{\mathfrak{sl}}(n)\)-module, \(E_w(\Lambda)\) which is called a Demazure module. Note that Demazure modules are finite dimensional, and also that they form a filtration on \(V(\Lambda)\) which is compatible with the Bruhat order on \(W\):

\[ w \leq w' \;\;\;\; \implies \;\;\;\; E_w(\Lambda) \subseteq E_{w'}(\Lambda) \]

We can also define Demazure operators that act on the group ring of the weight lattice \( P \):

\[ \Delta_i = {1 - e^{-\alpha_i}s_i \over 1 - e^{-\alpha_i}} \]

where \(s_i\) is the simple reflection in the Weyl group with respect to simple root \( \alpha_i\). To \( w \in W \) with reduced decomposition \( w = s_{i_1} s_{i_2} \dots s_{i_j} \) we can then associate the Demazure operator

\[\Delta_{w} = \Delta_{i_1} \Delta_{i_2} \dots \Delta_{i_j} \],

There is a nice connection between characters and Demazure operators given by the formula [2]:

\[\chi(E_w(\Lambda)) = \Delta_w(e^\Lambda). \]

The Connection

We let \(\Lambda_0, \Lambda_1, \dots, \Lambda_{n-1} \) be the \( n\)-fundamental weights of \( \widehat{\mathfrak{sl}}(n)\). Recall that these \( \Lambda_i \) are defined such that \((\Lambda_i, \alpha_j) = \delta_{ij}\). Finally,

\[ \delta = \sum^{n-1}_{i = 0} \alpha_i. \]

For the connection between \( E_\lambda \) and characters of Demazure modules we want to relate the action of \( \bar{H_i} \) and \( \Phi \) to operators on \( P \). More specifically, we would like a commutative diagram

We can get this by defining \( \pi: \mathbb{Z}[q,q^{-1}][z_1, \dots, z_n] \rightarrow P\) on generators by

\[ \pi(z_i) = e^{\Lambda_{i-1} - \Lambda_i}, \;\;\;\;\; \pi(z_n) = e^{\Lambda_{n-1} - \Lambda_0}, \;\;\;\;\; \pi(q) = e^{-\delta}. \]

(note that this definition is slightly different to that found in the paper). We get a similar commutative diagram for \( \Phi \):

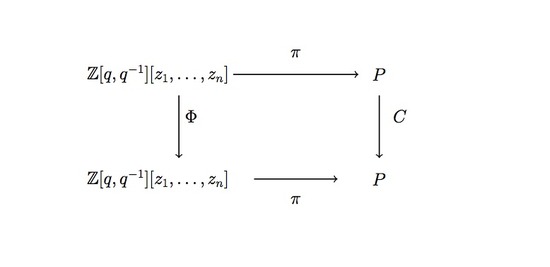
The main result of [3] is then that through the homomorphism \( \pi \), we can identify

\[ q^{-u(\lambda) + u(\eta_{\lambda})} E_\lambda \;\;\;\;\;\;\; \text{with} \;\;\;\;\;\;\; \chi(E_w(\Lambda_i))\]

where \(u(\lambda)\) and \(\eta_{\lambda}\) (this is a partition) depend only on \(\lambda\) and \(i = |\lambda| \text{mod}\; n\) and where \(w\) is an specific affine Weyl group element defined such that \(w\) acts on \(\eta_{|\lambda|}\) to give \(\lambda\).

References

1. J. Hong and S.J. Kang. Introduction to quantum groups and crystal bases, volume 42 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 2002.
2. S. Kumar, Demazure character formula in arbitrary Kac-Moody setting, Invent. Math. 89 (1987), 395-423.
3. Y. Sanderson, On the connection between Macdonald polynomials and Demazure characters, J. Algebraic Combin. 11 (2000), no.3, 269-275.