16.2: Vector Fields and Line Integrals: Work, Circulation, and Flux

Imagine putting a boat in a lake with random currents. The current at a particular point would hit the boat in a force at this point. At another point, the current is different so it would hit the boat with a different force. A grid of all these forces that his on the boat is called the vector field. Using the vector field, we can determine work,(the total water hitting the boat) circulation (the amount of water that would go in the same direction as the boat), and the flux (the amount of water that hits the boat) .

Vectors

A vector is a ray that starts at a point$(x,y,z)$ and goes in the direction $x \hat{\textbf{i}}+y \hat{\textbf{j}} +z \hat{\textbf{k}}$. A vector field is the compilation of these vectors at every point. We draw vector field with evenly spread points for visual purposes, but you should imagine the field as a continuum.

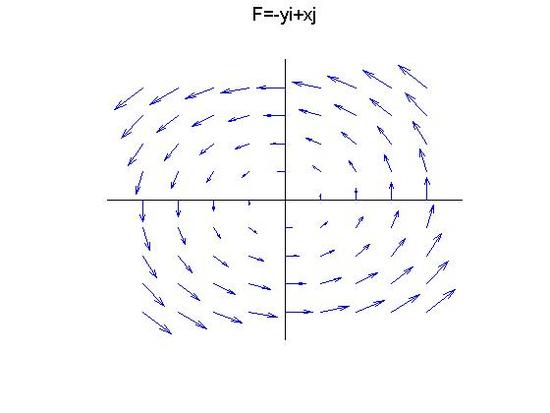
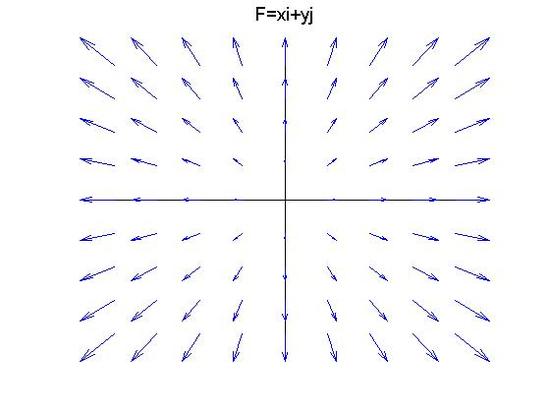
A vector field by itself has no meaning, but for the purpose of this section, we will call the field $F$ because force is a common use of the vector field. There are some methods you can use to figure out what a vector field looks like when given an equation

1. know what the vector field looks like
2. find a program that graphs vector fields
3. graph vectors at a number of points until you get a sense of what the graph looks like.
4. Use more advanced math you haven't learned yet

If you have no idea what a vector field looks like, you have to do it the hard way by plugging in points. This is a waste of time so it could be beneficial to memorize the common ones. Very rarely will you be required to know what a vector field looks like as long as you can solve the problem given. However, knowing what the vector field looks like can help identify if an answer is reasonable.

Work

This section assumes you know what work is, which is the sum of all the forces over the line

$$Work=\int_C F ds. \nonumber$$

This expression and those in the following sections can be solved using a line integral. This is the general equation but we can derive it a little more, start with an arbitrary force in parametric form $\vec{F}(x,y,z)$ and Newton's second law $\vec{F}=m\vec{a}$ we can convert $\vec{F} (x,y,z)$ into vector form $\vec{F}(\vec{r})$ to simplify the equation.

To get work over a line, the end result should be $\int_C \vec{F} dr$, the sum of the forces over the line $r(t)$.

First, change $\vec{a}$ into $\dfrac{dv}{dt}$ (the definition of acceleration)

$$\vec{F}=m\dfrac{dv}{dt} \nonumber$$

we will multiply both sides by $\vec{v}$. Notice that $\vec{v}$ is the same as $\dfrac{dr}{dt}$, so we can use this for the purpose of this proof

$$\vec{F} \cdot \dfrac{dr}{dt} = m \dfrac{dv}{dt} \cdot \vec{v} . \nonumber$$

Use the fundamental theorem of calculus to change form

$$\begin{align} \dfrac{dv}{dt}\cdot\vec{v} &= \dfrac{d}{dt} \int \vec{v}\dfrac{dv}{dt} \nonumber \\[4pt] &=\dfrac{d}{dt} \left ( \dfrac{\vec{v}\cdot\vec{v}}{2} \right) \nonumber \\[4pt] &=\dfrac{1}{2}\dfrac{d}{dt}\left ( \left | \vec v \right |^2 \right ). \end{align} \nonumber$$

Now put this back into the equation and we get

$$\vec{F}\cdot\dfrac{dr}{dt}=\dfrac{m}{2}\dfrac{d}{dt}\left | \vec v \right |^2. \nonumber$$

Integrate both sides with respect to time from time $0$ to time $T$

$$\int_0^T\vec{F}\cdot\dfrac{dr}{dt}dt=\dfrac{m}{2}\int_0^T\dfrac{d}{dt}\left | \vec v \right |^2dt \nonumber$$

$$\int_0^T\vec{F}\cdot dr=\dfrac{m}{2}d\int_0^T\left | \vec v \right |^2 . \nonumber$$

Notice that $\int_0^T\vec{F}\cdot dr$ is the line integral using the vector equation for the path. solving this equation yields

$$\int_0^T\vec{F}\cdot dr=\dfrac{m}{2}\left | \vec v(T) \right |^2-\dfrac{m}{2}\left | \vec v(0) \right |^2 \nonumber$$

This is the equation taught in physics classes. work is equal to change in kinetic energy

Flux

Flux is defined as the amount of "stuff" going through a curve or a surface and we can get the flux at a particular point by taking the force and seeing how much of the force is perpendicular to the curve. To do this we can find the normal vector, then take the dot product of the normal vector and force vector to see how much of the force vector is acting in the normal direction. Then we can add up all these points to get the total flux.

Thus the equation is

$$\int_C \vec{F}\cdot\hat{n} \,ds. \nonumber$$

This is the general equation but we can break this down a little more, the normal vector is perpendicular to the tangent vector and lies in the plane $\hat{n}=\hat{T}\times\hat{k}$ by including $k$ in the cross product, we ensure $\hat{n}$ is on the plane.

$$\hat{T}=\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt}\right |} \nonumber$$

$$ds=\left | \dfrac{dr}{dt} \right | dt \nonumber$$

This substitution is useful to know but is not used in breaking this equation down, so we can rewrite this equation as

$$\int_{t=a}^{t=b} \vec{F}\cdot \left(\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt}\right |}\times \hat{\textbf{k}} \right)ds \nonumber$$

$$\int_{t=a}^{t=b} \vec{F}\cdot \left(\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt}\right |}\times \hat{\textbf{k}}\right)ds. \nonumber$$

We can actually break down $\left(\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt}\right |}\times \hat{\textbf{k}} \right)$ even further:

$$\hat{T}=\left(\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt}\right |}\right)=\dfrac{dr}{ds} \nonumber$$

$$\dfrac{dr}{ds}=\dfrac{dx}{ds} \hat{\textbf{i}} +\dfrac{dy}{ds} \hat{\textbf{j}} . \nonumber$$

$$\hat{n}=\hat{T}\times \hat{\textbf{k}} =\dfrac{dx}{ds} \hat{\textbf{i}} +\dfrac{dy}{ds} \hat{\textbf{j}} \times \hat{\textbf{k}} =-\dfrac{dx}{ds} \hat{\textbf{j}} +\dfrac{dy}{ds} \hat{\textbf{i}} \nonumber$$

If we let $\vec{F}=M \hat{\textbf{i}} + N \hat{\textbf{j}}$ then we can rewrite the equation as:

$$\int_C \left ( M\dfrac{dy}{ds}-N\dfrac{dx}{ds}\right )ds =\int_C Mdy-Ndx. \nonumber$$

Example $\PageIndex{1}$: Gravity

What is the work done by force of gravity

$$\vec{F}=-\dfrac{\hat{r}}{\left | \vec{r} \right |^2} \nonumber$$

over a circular trajectory?

Solution

Since radius is not specified, we will use the variable $R$ for radius.

• we know the vector equation for a circle $\vec{r}(t)=R\; \cos(t) \hat{\textbf{i}} +R\; \sin(t) \hat{\textbf{j}}$
• we are given $F$ in terms of $r$ (if we were not given $F$ in terms of $r$ we would have to convert it because we need to integrate with respect to $r$
• we have the work equation $W=\int_0^T \vec{F}(r)\cdot d\vec{r}$
• we know that $T=2\pi$ because that is one rotation of a circle

Putting everything together we get the equation

$$W=\int_0^{2\pi} -\dfrac{\hat{r}}{\left | \vec{r} \right |^2}\cdot \dfrac{d\vec{r}}{dt}dt \nonumber$$

Lets break down each component.

Simplify $\left | \vec{r} \right |^2$:

$$\left | \vec{r} \right |^2=\sqrt{(R\cos(t)^2+(R\sin(t)^2)}^2=\left (\sqrt{R^2(\sin^2(t)+\cos^2(t))}\right )^2=(\sqrt{R^2(1)})^2=R^2. \nonumber$$

$\hat{r}$ is the unit vector of $\vec{r}$.

$$\begin{align} \hat{r}=\dfrac{\vec{r}}{\left | \vec{r} \right |}&=\dfrac{R\cos(t) \hat{\textbf{i}} +R\sin(t) \hat{\textbf{j}} }{\sqrt{R^2(\sin^2(t)+\cos^2(t))}} \nonumber \\[4pt] &= \dfrac{R\cos(t) \hat{\textbf{i}} +R\sin(t) \hat{\textbf{j}} }{\sqrt{R^2(1)}} \nonumber \\[4pt] &= \dfrac{R\cos(t) \hat{\textbf{i}} +R\sin(t) \hat{\textbf{j}} }{R} \nonumber \\[4pt] &=\cos(t) \hat{\textbf{i}} +\sin(t) \hat{\textbf{j}} \end{align} \nonumber$$

$\dfrac{d\vec{r}}{dt}$ is the derivative of $\vec{r}(t)$.

$$\dfrac{d\vec{r}}{dt}=\dfrac{d}{dt}\left (R\cos(t) \hat{\textbf{i}} +R\sin(t) \hat{\textbf{j}} \right)=-R\sin(t) \hat{\textbf{i}} +R\cos(t) \hat{\textbf{j}} \nonumber$$

$R$ is a constant so we can just move that out and substitute in our results for $\hat{r}$ and $d\vec{r}$.

$$W=-\dfrac{1}{R^2}\int_0^{2\pi} (\cos(t) \hat{\textbf{i}} +\sin(t) \hat{\textbf{j}} )\cdot (-R\sin(t) \hat{\textbf{i}} +R\cos(t)\ \hat{\textbf{j}} )dt \nonumber$$

The equation can just be solved using integrals.

$$\begin{align} W&=-\dfrac{1}{R^2}\int_0^{2\pi} (-R\sin(t)\cos(t) \hat{\textbf{i}} +R\cos(t)\sin(t) \hat{\textbf{j}} )dt \nonumber \\[4pt] &= -\dfrac{1}{R^2}\left [ \left(-R\dfrac{\sin^2(t)}{2}\right) \hat{\textbf{i}} +\left(R\dfrac{\sin^2(t)}{2}\right) \hat{\textbf{j}} \right ]_0^{2\pi} \nonumber \\[4pt] &= -\dfrac{1}{R^2} \left(-R\dfrac{\sin^2(2\pi)}{2}\right) \hat{\textbf{i}} +\left(R\dfrac{\sin^2(2\pi)}{2}\right) \hat{\textbf{j}} - \left(-R\dfrac{\sin^2(0)}{2}\right) \hat{\textbf{i}} -\left(R\dfrac{\sin^2(0)}{2}\right) \hat{\textbf{j}} \nonumber \\[4pt] &= -\dfrac{1}{R^2}(0 \hat{\textbf{i}} -0 \hat{\textbf{i}} +0 \hat{\textbf{j}} -0 \hat{\textbf{j}} )\nonumber \\[4pt] &=0 \end{align} \nonumber$$

Another way to look at this problem is to identify you are given the position vector($\vec(t)$ in a circle the velocity vector is tangent to the position vector so the cross product of $d(\vec{r})$ and $\vec{r}$ is 0 so the work is $0$.

Example $\PageIndex{2}$: Flux through a Square

Find the flux of $F=x \hat{\textbf{i}} +y \hat{\textbf{j}}$ through the square with side length 2.

Solution

First we need to parameterize the equation of the curve. Since this is a square we need four different equations. One of which is

$$r(t)=(1-t) \hat{\textbf{i}} + \hat{\textbf{j}} \;\;\;\;0\leq t\leq 2. \nonumber$$

Next find $\dfrac{dr}{dt}$, the unit tangent vector of $r$

$$\dfrac{dr}{dt}=\dfrac{d}{dt}(1-t) \hat{\textbf{i}} +\dfrac{d}{dt} \hat{\textbf{j}} = - \hat{\textbf{i}} \nonumber$$

$$\hat{T}=\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt} \right |}=\dfrac{- \hat{\textbf{i}} }{1}=-\hat{ \hat{\textbf{i}} }. \nonumber$$

Then find the unit normal vector which is defined as $\hat{n}=\hat{T} \times \hat{\textbf{k}}$

$$\hat{n}=- \hat{\textbf{i}} \times \hat{\textbf{k}} = \hat{\textbf{j}} . \nonumber$$

Now we have everything required to solve for the flux $\int_C F\cdot\hat{n} ds$

$$\int_C (x(t) \hat{\textbf{i}} dx +y(t) \hat{\textbf{j}} )\cdot \hat{\textbf{j}} \left |\dfrac{dr}{dt}\right | dt \nonumber$$

$$\int_0^2 0 \hat{\textbf{i}} +y(t) \hat{\textbf{j}} (1) dt = 2. \nonumber$$

We found the flux this side to be 2. For any other problems, we would need to calculate the other three lines and add them up. But for this specific problem, the force is outward from the center so the other three sides have the same flux. making the answer $2 \times 4 = 8$.

Example $\PageIndex{3}$: Flux through a Circle

Find the flux of $F=x \hat{\textbf{i}} +y \hat{\textbf{j}}$ through a circle with radius = $R$.

Solution

First, parameterize the curve:

$$r(t)=R\cos(t) \hat{\textbf{i}} +R\sin(t) \hat{\textbf{j}} \; \;\;\;0\leq t \leq 2\pi \;\;\text{or}\;\; x(t)=R\cos(t) \hat{\textbf{i}} \;\;y(t)=R\sin(t) \hat{\textbf{j}}. \nonumber$$

Then the unit tangent vector $\hat{T}$:

$$\dfrac{dr}{dt}=\dfrac{d}{dt}R\cos(t) \hat{\textbf{i}} +\dfrac{d}{dt}R\sin(t) \hat{\textbf{j}} = -R\sin(t) \hat{\textbf{i}} + R\cos(t) \hat{\textbf{j}} \nonumber$$

$$\left | \dfrac{dr}{dt} \right |=\sqrt{\left ( \dfrac{dx}{dt} \right )^2 +\left ( \dfrac{dy}{dt} \right )^2}=\sqrt{(-\sin(t)^2+\cos(t)^2}=\sqrt{R^2\cos^2(t)+R^2\sin^2(t)} =R \nonumber$$

$$\hat{T}=\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt} \right |}=\dfrac{R-\sin(t) \hat{\textbf{i}} + R\cos(t) \hat{\textbf{j}} }{R}= -\sin(t) \hat{\textbf{i}} + \cos(t) \hat{\textbf{j}}. \nonumber$$

Find the unit normal vector $\hat{n}=\hat{T} \times \hat{\textbf{k}}$:

$$\hat{n}=(-\sin(t)+\cos(t))\times \hat{\textbf{k}} \nonumber$$

$$\hat{n}=\sin(t) \hat{\textbf{j}} +\cos(t) \hat{\textbf{i}}. \nonumber$$

Solve for the flux $\int_C F\cdot\hat{n} ds$:

$$\int_C (x(t) \hat{\textbf{i}} +y(t))\cdot \sin(t) \hat{\textbf{j}} +\cos(t) \hat{\textbf{i}} \left |\dfrac{dr}{dt}\right | dt \nonumber$$

$$\int_0^{2\pi} (x(t) \hat{\textbf{i}} +y(t))\cdot \sin(t) \hat{\textbf{j}} +\cos(t) \hat{\textbf{i}} (R)dt \nonumber$$

$$\int_0^{2\pi} (x(t)\cos(t) + y(t)\sin(t))Rdt. \nonumber$$

Substitute in for $x(t)$ and $y(t)$

$$\begin{align} &\int_0^{2\pi} (R\cos(t)\cos(t) + R\sin(t)\sin(t))(R)dt \nonumber \\[4pt] &= \int_0^{2\pi} (R^2)dt \nonumber \\[4pt] &= R^2\left [t\right ]_0^{2\pi} \nonumber \\[4pt] &=2\pi R^2 . \end{align} \nonumber$$

Example $\PageIndex{5}$: Flux through an Ellipse

Find the flux of $F=x \hat{\textbf{i}} +y \hat{\textbf{j}}$ through an ellipse with axes $a$ and $b$.

Solution

Start off by parameterizing the curve of an ellipse

$$\vec{r}(t)=a\cos(t) \hat{\textbf{i}} +b\sin(t) \hat{\textbf{j}}. \nonumber$$

Then, find the unit tangent vector

$$\vec{T}=\dfrac{dr}{dt}=-a\sin(t) \hat{\textbf{i}} +b\cos(t) \hat{\textbf{j}} \nonumber$$

$$\left | \dfrac{dr}{dt} \right |=\sqrt{(-a\sin(t))^2+(b\cos(t))^2}=..... \nonumber$$

so solving for $\left | \dfrac{dr}{dt} \right |$ might take up too much time so for now we're just going to leave it as it is

$$\hat{T}=\dfrac{\dfrac{dr}{dt}}{\left | \dfrac{dr}{dt} \right |}=\dfrac{-a\sin(t) \hat{\textbf{i}} +b\cos(t) \hat{\textbf{j}} }{\left | \dfrac{dr}{dt} \right |} \nonumber$$

Now we take cross product with $\hat{k}$ to get $\hat{n}$

$$\hat{n}=\dfrac{-a\sin(t) \hat{\textbf{i}} +b\cos(t) \hat{\textbf{j}} }{\left | \dfrac{dr}{dt} \right |}\times \hat{\textbf{k}} =\dfrac{b\cos(t) \hat{\textbf{i}} +a\sin(t) \hat{\textbf{j}} }{\left | \dfrac{dr}{dt} \right |}. \nonumber$$

Now just solve for flux

$$\begin{align} & \int_C \vec{F}(r(t))\cdot \hat{n}ds \nonumber \\[4pt] &= \int_0^{2\pi} (x \hat{\textbf{i}} +y \hat{\textbf{j}} )\cdot \left (\dfrac{b\cos(t) \hat{\textbf{i}} +a\sin(t) \hat{\textbf{j}} }{\left | \dfrac{dr}{dt} \right |}\right ) \left (\left | \dfrac{dr}{dt} \right |\right )dt \nonumber \\[4pt] &= \int_0^{2\pi} (a\cos(t) \hat{\textbf{i}} +b(\sin(t) \hat{\textbf{j}} )\cdot \left (\dfrac{b\cos(t) \hat{\textbf{i}} +a\sin(t) \hat{\textbf{j}} }{\left | \dfrac{dr}{dt} \right |}\right ) \left (\left | \dfrac{dr}{dt} \right |\right )dt. \end{align} \nonumber$$

Notice that $\left | \dfrac{dr}{dt} \right|$ cancels out and we're left with

$$\begin{align} \int_0^{2\pi} a^2\cos^2(t)+b^2\sin^2(t) dt \nonumber \\[4pt] &= \int_0^{2\pi} a^2+b^2 dt \nonumber \\[4pt] &= 2\pi(a^2+b^2). \end{align} \nonumber$$

Circulation

Circulation is the amount of "stuff" parallel to the direction of motion. We are looking for the amount of "stuff going" in the direction of the tangent vector and we calculate that by taking the dot product of $\vec{F}$ (The vector field) and $\hat T$ (the direction that is tangent to the curve) We'll use $\Gamma$ as the variable for circulation

$$\Gamma=\int_C \vec{F}\cdot\hat{T} ds. \nonumber$$

Example $\PageIndex{5}$: Circulation

Given the vector field $\vec{F}(\vec{r})=-y \hat{\textbf{i}} +x \hat{\textbf{j}}$ find circulation over a circle.

Solution

Parameterize the equation for a circle

$$a\cos(t) \hat{\textbf{i}} +a\sin(t) \hat{\textbf{j}} \;\;\;\;x(t)=R\cos(t)\;\; y(t)=R\sin(t) \nonumber$$

Then find $\hat{T}$

$$\vec{T}=\dfrac{dr}{dt}=-R\sin(t) \hat{\textbf{i}} +R\cos(t) \hat{\textbf{j}} \nonumber$$

$$\left | \vec{T} \right |=\sqrt{(R\sin(t))^2+(R\cos(t))^2}=R \nonumber$$

$$\hat{T}=\dfrac{\vec{T}}{\left | \vec{T} \right |}=\dfrac{-R\sin(t) \hat{\textbf{i}} +R\cos(t) \hat{\textbf{j}} }{R}=-\sin(t) \hat{\textbf{i}} +\cos(t) \hat{\textbf{j}}. \nonumber$$

Then calculate for circulation

$$\begin{align} \Gamma=\int_C \vec{F}\cdot \hat{T} ds &=\int_C \vec{F}\cdot \hat{T}\left |\dfrac{dr}{dt}\right |dt \nonumber \\[4pt] &=\int_C \left ( -R\sin(t) \hat{\textbf{i}} +R\cos(t) \hat{\textbf{j}} \right )\cdot \left (-\sin(t) \hat{\textbf{i}} +\cos(t) \hat{\textbf{j}} \right ) (R)dt \nonumber \\[4pt] &= \int_0^{2\pi} \left (R\sin^2(t)+R\cos^2(t)\right)Rdt \nonumber \\[4pt] &= \int_0^{2\pi} R^2dt=2\pi R^2 . \end{align} \nonumber$$

Contributors and Attributions

• Danny Nguyen (UCD)

• Integrated by Justin Marshall.