2.5: Continuity
- Page ID
- 8222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explain the three conditions for continuity at a point.
- Describe three kinds of discontinuities.
- Define continuity on an interval.
- State the theorem for limits of composite functions.
- Provide an example of the intermediate value theorem.
Many functions have the property that their graphs can be traced with a pencil without lifting the pencil from the page. Such functions are called continuous. Other functions have points at which a break in the graph occurs, but satisfy this property over intervals contained in their domains. They are continuous on these intervals and are said to have a discontinuity at a point where a break occurs.
We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point.
Continuity at a Point
Before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. We then create a list of conditions that prevent such failures.
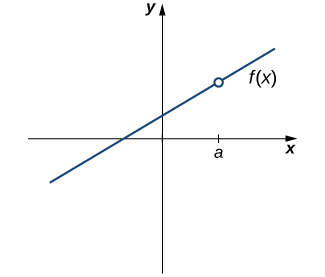
Our first function of interest is shown in Figure \(\PageIndex{1}\). We see that the graph of \(f(x)\) has a hole at \(a\). In fact, \(f(a)\) is undefined. At the very least, for \(f(x)\) to be continuous at \(a\), we need the following condition:
i. \(f(a)\) is defined
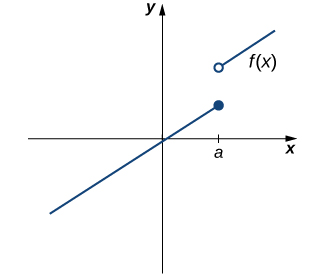
However, as we see in Figure \(\PageIndex{2}\), this condition alone is insufficient to guarantee continuity at the point \(a\). Although \(f(a)\) is defined, the function has a gap at \(a\). In this example, the gap exists because \(\displaystyle \lim_{x→a}f(x)\) does not exist. We must add another condition for continuity at \(a\)—namely,
ii. \(\displaystyle \lim_{x→a}f(x)\) exists
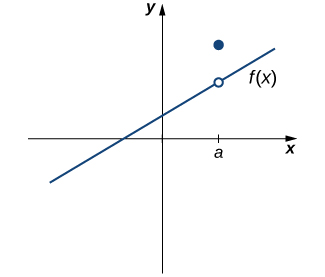
However, as we see in Figure \(\PageIndex{3}\), these two conditions by themselves do not guarantee continuity at a point. The function in this figure satisfies both of our first two conditions, but is still not continuous at \(a\). We must add a third condition to our list:
iii. \(\displaystyle \lim_{x→a}f(x)=f(a)\)
Now we put our list of conditions together and form a definition of continuity at a point.
A function \(f(x)\) is continuous at a point \(a\) if and only if the following three conditions are satisfied:
- \(f(a)\) is defined
- \(\displaystyle \lim_{x→a}f(x)\) exists
- \(\displaystyle \lim_{x→a}f(x)=f(a)\)
A function is discontinuous at a point \(a\) if it fails to be continuous at \(a\).
The following procedure can be used to analyze the continuity of a function at a point using this definition.
- Check to see if \(f(a)\) is defined. If \(f(a)\) is undefined, we need go no further. The function is not continuous at \(a.\) If \(f(a)\) is defined, continue to step 2.
- Compute \(\displaystyle \lim_{x→a}f(x)\). In some cases, we may need to do this by first computing \(\displaystyle \lim_{x→a^−}f(x)\) and \(\displaystyle \lim_{x→a^+}f(x)\). If \(\displaystyle \lim_{x→a}f(x)\) does not exist (that is, it is not a real number), then the function is not continuous at \(a\) and the problem is solved. If \(\displaystyle \lim_{x→a}f(x)\) exists, then continue to step 3.
- Compare \(f(a)\) and \(\displaystyle \lim_{x→a}f(x)\). If \(\displaystyle \lim_{x→a}f(x)≠f(a)\), then the function is not continuous at \(a.\) If \(\displaystyle \lim_{x→a}f(x)=f(a)\), then the function is continuous at \(a.\)
The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.
Using the definition, determine whether the function \(f(x)=\dfrac{x^2−4}{x−2}\) is continuous at \(x=2\). Justify the conclusion.
Solution
Let’s begin by trying to calculate \(f(2)\). We can see that \(f(2)=0/0\), which is undefined. Therefore, \(f(x)=\dfrac{x^2−4}{x−2}\) is discontinuous at \(2\) because \(f(2)\) is undefined. The graph of \(f(x)\) is shown in Figure \(\PageIndex{4}\).

Using the definition, determine whether the function \(f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}\) is continuous at \(x=3\). Justify the conclusion.
Solution
Let’s begin by trying to calculate \(f(3)\).
\(f(3)=−(3^2)+4=−5\).
Thus, \(f(3)\) is defined. Next, we calculate \(\displaystyle \lim_{x→3}f(x)\). To do this, we must compute \(\displaystyle \lim_{x→3^−}f(x)\) and \( \displaystyle \lim_{x→3^+}f(x)\):
\(\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5\)
and
\(\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4\).
Therefore, \(\displaystyle \lim_{x→3}f(x)\) does not exist. Thus, \(f(x)\) is not continuous at 3. The graph of \(f(x)\) is shown in Figure \(\PageIndex{5}\).
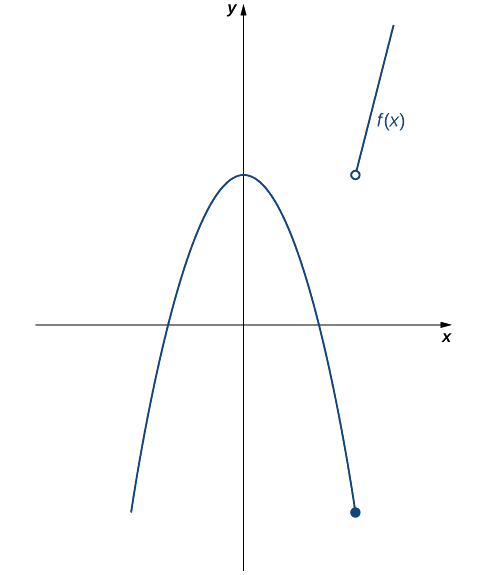
Using the definition, determine whether the function \(f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}\) is continuous at \(x=0\).
Solution
First, observe that
\(f(0)=1\)
Next,
\(\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1\).
Last, compare \(f(0)\) and \(\displaystyle \lim_{x→0}f(x)\). We see that
\(\displaystyle f(0)=1=\lim_{x→0}f(x)\).
Since all three of the conditions in the definition of continuity are satisfied, \(f(x)\) is continuous at \(x=0\).
Using the definition, determine whether the function \(f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}\) is continuous at \(x=1\). If the function is not continuous at 1, indicate the condition for continuity at a point that fails to hold.
- Hint
-
Check each condition of the definition.
- Answer
-
\(f\) is not continuous at \(1\) because \(\displaystyle f(1)=2≠3=\lim_{x→1}f(x)\).
By applying the definition of continuity and previously established theorems concerning the evaluation of limits, we can state the following theorem.
Polynomials and rational functions are continuous at every point in their domains.
Previously, we showed that if \(p(x)\) and \(q(x)\) are polynomials, \(\displaystyle \lim_{x→a}p(x)=p(a)\) for every polynomial \(p(x)\) and \(\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) as long as \(q(a)≠0\). Therefore, polynomials and rational functions are continuous on their domains.
□
We now apply Theorem \(\PageIndex{1}\) to determine the points at which a given rational function is continuous.
For what values of x is \(f(x)=\dfrac{x+1}{x−5}\) continuous?
Solution
The rational function \(f(x)=\dfrac{x+1}{x−5}\) is continuous for every value of \(x\) except \(x=5\).
For what values of \(x\) is \(f(x)=3x^4−4x^2\) continuous?
- Hint
-
Use the Continuity of Polynomials and Rational Functions stated above.
- Answer
-
\(f(x)\) is continuous at every real number.
Types of Discontinuities
As we have seen in Example \(\PageIndex{1A}\) and Example \(\PageIndex{1B}\), discontinuities take on several different appearances. We classify the types of discontinuities we have seen thus far as removable discontinuities, infinite discontinuities, or jump discontinuities. Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote. Figure \(\PageIndex{6}\) illustrates the differences in these types of discontinuities. Although these terms provide a handy way of describing three common types of discontinuities, keep in mind that not all discontinuities fit neatly into these categories.
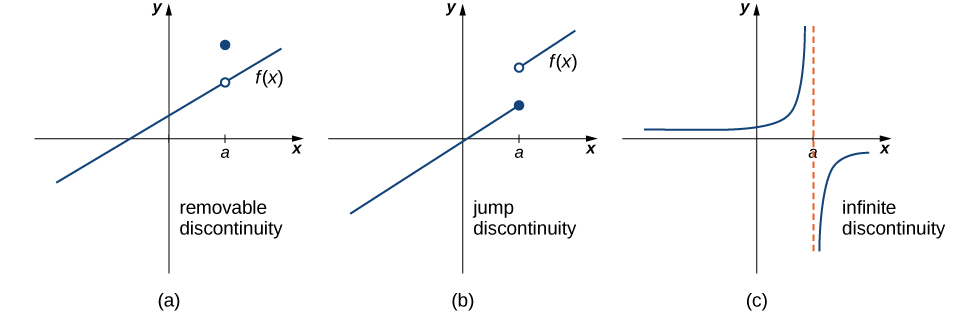
These three discontinuities are formally defined as follows:
If \(f(x)\) is discontinuous at \(a,\) then
1. \(f\) has a removable discontinuity at \(a\) if \(\displaystyle \lim_{x→a}f(x)\) exists. (Note: When we state that \(\displaystyle \lim_{x→a}f(x)\) exists, we mean that \(\displaystyle \lim_{x→a}f(x)=L\), where \(L\) is a real number.)
2. \(f\) has a jump discontinuity at \(a\) if \(\displaystyle \lim_{x→a^−}f(x)\) and \(\displaystyle \lim_{x→a^+}f(x)\) both exist, but \(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\). (Note: When we state that \(\displaystyle \lim_{x→a^−}f(x)\) and \(\displaystyle \lim_{x→a^+}f(x)\) both exist, we mean that both are real-valued and that neither take on the values \(±∞\).)
3. \(f\) has an infinite discontinuity at \(a\) if \(\displaystyle \lim_{x→a^−}f(x)=±∞\) or \(\displaystyle \lim_{x→a^+}f(x)=±∞\).
In Example \(\PageIndex{1A},\) we showed that \(f(x)=\dfrac{x^2−4}{x−2}\) is discontinuous at \(x=2\). Classify this discontinuity as removable, jump, or infinite.
Solution
To classify the discontinuity at \(2\) we must evaluate \(\displaystyle \lim_{x→2}f(x)\):
\(\displaystyle \begin{align*} \lim_{x→2}f(x) &=\lim_{x→2}\frac{x^2−4}{x−2}\\[4pt]
&= \lim_{x→2}\frac{(x−2)(x+2)}{x−2}\\[4pt]
&= \lim_{x→2}(x+2)\\[4pt]
&=4.\end{align*}\)
Since \(f\) is discontinuous at \(2\) and \(\displaystyle \lim_{x→2}f(x)\) exists, \(f\) has a removable discontinuity at \(x=2\).
In Example \(\PageIndex{1B}\), we showed that \(f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}\) is discontinuous at \(x=3\). Classify this discontinuity as removable, jump, or infinite.
Solution
Earlier, we showed that \(f\) is discontinuous at \(3\) because \(\displaystyle \lim_{x→3}f(x)\) does not exist. However, since \(\displaystyle \lim_{x→3^−}f(x)=−5\) and \(\displaystyle \lim_{x→3^+}f(x)=4\) both exist, we conclude that the function has a jump discontinuity at \(3\).
Determine whether \(f(x)=\dfrac{x+2}{x+1}\) is continuous at \(−1\). If the function is discontinuous at \(−1\), classify the discontinuity as removable, jump, or infinite.
Solution
The function value \(f(−1)\) is undefined. Therefore, the function is not continuous at \(−1\). To determine the type of discontinuity, we must determine the limit at \(−1\). We see that \(\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞\) and \(\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞\). Therefore, the function has an infinite discontinuity at \(−1\).
For \(f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}\), decide whether \(f\) is continuous at \(1\). If \(f\) is not continuous at \(1\), classify the discontinuity as removable, jump, or infinite.
- Hint
-
Consider the definitions of the various kinds of discontinuity stated above. If the function is discontinuous at \(1\), look at \(\displaystyle \lim_{x→1}f(x)\)
- Answer
-
Discontinuous at \(1\); removable
Continuity over an Interval
Now that we have explored the concept of continuity at a point, we extend that idea to continuity over an interval. As we develop this idea for different types of intervals, it may be useful to keep in mind the intuitive idea that a function is continuous over an interval if we can use a pencil to trace the function between any two points in the interval without lifting the pencil from the paper. In preparation for defining continuity on an interval, we begin by looking at the definition of what it means for a function to be continuous from the right at a point and continuous from the left at a point.
A function \(f(x)\) is said to be continuous from the right at \(a\) if \(\displaystyle \lim_{x→a^+}f(x)=f(a)\).
A function \(f(x)\) is said to be continuous from the left at \(a\) if \(\displaystyle \lim_{x→a^−}f(x)=f(a)\)
A function is continuous over an open interval if it is continuous at every point in the interval. A function \(f(x)\) is continuous over a closed interval of the form \([a,b]\) if it is continuous at every point in \((a,b)\) and is continuous from the right at \(a\) and is continuous from the left at \(b.\) Analogously, a function \(f(x)\) is continuous over an interval of the form \((a,b]\) if it is continuous over \((a,b)\) and is continuous from the left at \(b.\) Continuity over other types of intervals are defined in a similar fashion.
Requiring that \(\displaystyle \lim_{x→a^+}f(x)=f(a)\) and \(\displaystyle \lim_{x→b^−}f(x)=f(b)\) ensures that we can trace the graph of the function from the point \((a,f(a))\) to the point \((b,f(b))\) without lifting the pencil. If, for example, \(\displaystyle \lim_{x→a^+}f(x)≠f(a)\), we would need to lift our pencil to jump from \(f(a)\) to the graph of the rest of the function over \((a,b]\).
State the interval(s) over which the function \(f(x)=\dfrac{x−1}{x^2+2x}\) is continuous.
Solution
Since \(f(x)=\dfrac{x−1}{x^2+2x}\) is a rational function, it is continuous at every point in its domain. The domain of \(f(x)\) is the set \((−∞,−2)∪(−2,0)∪(0,+∞)\). Thus, \(f(x)\) is continuous over each of the intervals \((−∞,−2),(−2,0)\), and \((0,+∞)\).
State the interval(s) over which the function \(f(x)=\sqrt{4−x^2}\) is continuous.
Solution
From the limit laws, we know that \(\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}\) for all values of a in \((−2,2)\). We also know that \(\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0\) exists and \(\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0\) exists. Therefore, \(f(x)\) is continuous over the interval \([−2,2]\).
State the interval(s) over which the function \(f(x)=\sqrt{x+3}\) is continuous.
- Hint
-
Use Example \(\PageIndex{7}\) as a guide.
- Answer
-
\([−3,+∞)\)
Theorem \(\PageIndex{2}\) allows us to expand our ability to compute limits. In particular, this theorem ultimately allows us to demonstrate that trigonometric functions are continuous over their domains.
If \(f(x)\) is continuous at \(L\) and \(\displaystyle \lim_{x→a}g(x)=L\), then
\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).\)
Before we move on to Example \(\PageIndex{8},\) recall that earlier, in the section on limit laws, we showed \(\displaystyle \lim_{x→0}\cos x=1=\cos(0)\). Consequently, we know that \(f(x)=\cos x\) is continuous at \(0\). In Example \(\PageIndex{8},\) we see how to combine this result with the composite function theorem.
Evaluate \(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)\).
Solution
The given function is a composite of \(\cos x\) and \(x−\frac{π}{2}\). Since \(\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0\) and \(\cos x\) is continuous at \(0\), we may apply the composite function theorem. Thus,
\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.\)
Evaluate \(\displaystyle \lim_{x→π}\sin(x−π)\).
- Hint
-
\(f(x)=\sin x\) is continuous at \(0\). Use Example \(\PageIndex{8}\) as a guide.
- Answer
-
\(0\)
The proof of the next theorem uses the composite function theorem as well as the continuity of \(f(x)=\sin x\) and \(g(x)=\cos x\) at the point \(0\) to show that trigonometric functions are continuous over their entire domains.
Trigonometric functions are continuous over their entire domains.
We begin by demonstrating that \(\cos x\) is continuous at every real number. To do this, we must show that \(\displaystyle \lim_{x→a}\cos x=\cos a\) for all values of \(a\).
\(\displaystyle \begin{align*} \lim_{x→a}\cos x &=\lim_{x→a}\cos((x−a)+a) & & \text{Rewrite }x=x−a+a.\\[4pt]
&= \lim_{x→a}(\cos(x−a)\cos a−\sin(x−a)\sin a) & & \text{Apply the identity for the cosine of the sum of two angles.}\\[4pt]
&= \cos(\lim_{x→a}(x−a))\cos a−\sin(\lim_{x→a}(x−a))\sin a & &\text{Since }\lim_{x→a}(x−a)=0,\text{ and }\sin x\text{ and }\cos x\text{ are continuous at }0.\\[4pt]
&= \cos(0)\cos a−\sin(0)\sin a & & \text{Evaluate }\cos(0)\text{ and }\sin(0)\text{ and simplify.}\\[4pt]
&= 1⋅\cos a−0⋅\sin a=\cos a. \end{align*}\)
The proof that \(\sin x\) is continuous at every real number is analogous. Because the remaining trigonometric functions may be expressed in terms of \(\sin x\) and \(\cos x\), their continuity follows from the quotient limit law.
□
As you can see, the composite function theorem is invaluable in demonstrating the continuity of trigonometric functions. As we continue our study of calculus, we revisit this theorem many times.
The Intermediate Value Theorem
Functions that are continuous over intervals of the form \([a,b]\), where \(a\) and \(b\) are real numbers, exhibit many useful properties. Throughout our study of calculus, we will encounter many powerful theorems concerning such functions. The first of these theorems is the Intermediate Value Theorem.
Let \(f\) be continuous over a closed, bounded interval \([a,b]\). If \(z\) is any real number between \(f(a)\) and \(f(b)\), then there is a number \(c\) in \([a,b]\) satisfying \(f(c)=z\) in Figure \(\PageIndex{7}\).
![A diagram illustrating the intermediate value theorem. There is a generic continuous curved function shown over the interval [a,b]. The points fa. and fb. are marked, and dotted lines are drawn from a, b, fa., and fb. to the points (a, fa.) and (b, fb.). A third point, c, is plotted between a and b. Since the function is continuous, there is a value for fc. along the curve, and a line is drawn from c to (c, fc.) and from (c, fc.) to fc., which is labeled as z on the y axis.](https://math.libretexts.org/@api/deki/files/12348/2.4.3.png?revision=1)
Show that \(f(x)=x−\cos x\) has at least one zero.
Solution
Since \(f(x)=x−\cos x\) is continuous over \((−∞,+∞)\), it is continuous over any closed interval of the form \([a,b]\). If you can find an interval \([a,b]\) such that \(f(a)\) and \(f(b)\) have opposite signs, you can use the Intermediate Value Theorem to conclude there must be a real number \(c\) in \((a,b)\) that satisfies \(f(c)=0\). Note that
\(f(0)=0−\cos(0)=−1<0\)
and
\(f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0\).
Using the Intermediate Value Theorem, we can see that there must be a real number \(c\) in \([0,π/2]\) that satisfies \(f(c)=0\). Therefore, \(f(x)=x−\cos x\) has at least one zero.
If \(f(x)\) is continuous over \([0,2],f(0)>0\) and \(f(2)>0\), can we use the Intermediate Value Theorem to conclude that \(f(x)\) has no zeros in the interval \([0,2]\)? Explain.
Solution
No. The Intermediate Value Theorem only allows us to conclude that we can find a value between \(f(0)\) and \(f(2)\); it doesn’t allow us to conclude that we can’t find other values. To see this more clearly, consider the function \(f(x)=(x−1)^2\). It satisfies \(f(0)=1>0,f(2)=1>0\), and \(f(1)=0\).
For \(f(x)=1/x,f(−1)=−1<0\) and \(f(1)=1>0\). Can we conclude that \(f(x)\) has a zero in the interval \([−1,1]\)?
Solution
No. The function is not continuous over \([−1,1]\). The Intermediate Value Theorem does not apply here.
Show that \(f(x)=x^3−x^2−3x+1\) has a zero over the interval \([0,1]\).
- Hint
-
Find \(f(0)\) and \(f(1)\). Apply the Intermediate Value Theorem.
- Answer
-
\(f(0)=1>0,\;f(1)=−2<0;\;f(x)\) is continuous over \([0,1]\). It must have a zero on this interval.
Key Concepts
- For a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at that point must equal the value of the limit at that point.
- Discontinuities may be classified as removable, jump, or infinite.
- A function is continuous over an open interval if it is continuous at every point in the interval. It is continuous over a closed interval if it is continuous at every point in its interior and is continuous at its endpoints.
- The composite function theorem states: If \(f(x)\) is continuous at L and \(\displaystyle \lim_{x→a}g(x)=L\), then \(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)\).
- The Intermediate Value Theorem guarantees that if a function is continuous over a closed interval, then the function takes on every value between the values at its endpoints.
Glossary
- continuity at a point
- A function \(f(x)\) is continuous at a point \(a\) if and only if the following three conditions are satisfied: (1) \(f(a)\) is defined, (2) \(\displaystyle \lim_{x→a}f(x)\) exists, and (3) \(\displaystyle \lim{x→a}f(x)=f(a)\)
- continuity from the left
- A function is continuous from the left at \(b\) if \(\displaystyle \lim_{x→b^−}f(x)=f(b)\)
- continuity from the right
- A function is continuous from the right at \(a\) if \(\displaystyle \lim_{x→a^+}f(x)=f(a)\)
- continuity over an interval
- a function that can be traced with a pencil without lifting the pencil; a function is continuous over an open interval if it is continuous at every point in the interval; a function \(f(x)\) is continuous over a closed interval of the form [\(a,b\)] if it is continuous at every point in (\(a,b\)), and it is continuous from the right at \(a\) and from the left at \(b\)
- discontinuity at a point
- A function is discontinuous at a point or has a discontinuity at a point if it is not continuous at the point
- infinite discontinuity
- An infinite discontinuity occurs at a point \(a\) if \(\displaystyle \lim_{x→a^−}f(x)=±∞\) or \(\displaystyle \lim_{x→a^+}f(x)=±∞\)
- Intermediate Value Theorem
- Let \(f\) be continuous over a closed bounded interval [\(a,b\)] if \(z\) is any real number between \(f(a)\) and \(f(b)\), then there is a number \(c\) in [\(a,b\)] satisfying \(f(c)=z\)
- jump discontinuity
- A jump discontinuity occurs at a point \(a\) if \(\displaystyle \lim_{x→a^−}f(x)\) and \(\displaystyle \lim_{x→a^+}f(x)\) both exist, but \(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\)
- removable discontinuity
- A removable discontinuity occurs at a point \(a\) if \(f(x)\) is discontinuous at \(a\), but \(\displaystyle \lim_{x→a}f(x)\) exists

