6.6: Moments and Centers of Mass
- Page ID
- 8167
- Find the center of mass of objects distributed along a line.
- Locate the center of mass of a thin plate.
- Use symmetry to help locate the centroid of a thin plate.
- Apply the theorem of Pappus for volume.
In this section, we consider centers of mass (also called centroids, under certain conditions) and moments. The basic idea of the center of mass is the notion of a balancing point. Many of us have seen performers who spin plates on the ends of sticks. The performers try to keep several of them spinning without allowing any of them to drop. If we look at a single plate (without spinning it), there is a sweet spot on the plate where it balances perfectly on the stick. If we put the stick anywhere other than that sweet spot, the plate does not balance and it falls to the ground. (That is why performers spin the plates; the spin helps keep the plates from falling even if the stick is not exactly in the right place.) Mathematically, that sweet spot is called the center of mass of the plate.
In this section, we first examine these concepts in a one-dimensional context, then expand our development to consider centers of mass of two-dimensional regions and symmetry. Last, we use centroids to find the volume of certain solids by applying the theorem of Pappus.
Center of Mass and Moments
Let’s begin by looking at the center of mass in a one-dimensional context. Consider a long, thin wire or rod of negligible mass resting on a fulcrum, as shown in Figure \(\PageIndex{1a}\). Now suppose we place objects having masses \(m_1\) and \(m_2\) at distances \(d_1\) and \(d_2\) from the fulcrum, respectively, as shown in Figure \(\PageIndex{1b}\).
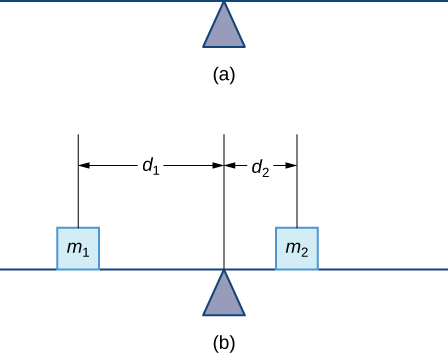
The most common real-life example of a system like this is a playground seesaw, or teeter-totter, with children of different weights sitting at different distances from the center. On a seesaw, if one child sits at each end, the heavier child sinks down and the lighter child is lifted into the air. If the heavier child slides in toward the center, though, the seesaw balances. Applying this concept to the masses on the rod, we note that the masses balance each other if and only if
\[m_1d_1=m_2d_2. \nonumber \]
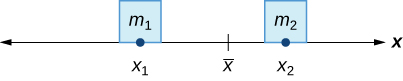
In the seesaw example, we balanced the system by moving the masses (children) with respect to the fulcrum. However, we are really interested in systems in which the masses are not allowed to move, and instead we balance the system by moving the fulcrum. Suppose we have two point masses, \(m_1\) and \(m_2\), located on a number line at points \(x_1\) and \(x_2\), respectively (Figure \(\PageIndex{2}\)). The center of mass, \(\bar{x}\), is the point where the fulcrum should be placed to make the system balance.
Thus, we have
\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]
or
\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]
The expression in the numerator of Equation \ref{COM}, \(m_1x_1+m_2x_2\), is called the first moment of the system with respect to the origin. If the context is clear, we often drop the word first and just refer to this expression as the moment of the system. The expression in the denominator, \(m_1+m_2\), is the total mass of the system. Thus, the center of mass of the system is the point at which the total mass of the system could be concentrated without changing the moment.
This idea is not limited just to two point masses. In general, if \(n\) masses, \(m_1,m_2,…,m_n,\) are placed on a number line at points \(x_1,x_2,…,x_n,\) respectively, then the center of mass of the system is given by
\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]
Let \(m_1,m_2,…,m_n\) be point masses placed on a number line at points \(x_1,x_2,…,x_n\), respectively, and let \(\displaystyle m=\sum_{i=1}^nm_i\) denote the total mass of the system. Then, the moment of the system with respect to the origin is given by
\[M=\sum_{i=1}^nm_ix_i \label{moment} \]
and the center of mass of the system is given by
\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]
We apply this theorem in the following example.
Suppose four point masses are placed on a number line as follows:
- \(m_1=30\,kg,\) placed at \(x_1=−2m\)
- \(m_2=5\,kg,\) placed at \(x_2=3m\)
- \(m_3=10\,kg,\) placed at \(x_3=6m\)
- \(m_4=15\,kg,\) placed at \(x_4=−3m.\)
Solution
Find the moment of the system with respect to the origin and find the center of mass of the system.
First, we need to calculate the moment of the system (Equation \ref{moment}):
\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]
Now, to find the center of mass, we need the total mass of the system:
\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]
Then we have (from Equation \ref{COM2a})
\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).
The center of mass is located 1/2 m to the left of the origin.
Suppose four point masses are placed on a number line as follows:
- \(m_1=12\,kg\) placed at \(x_1=−4m\)
- \(m_2=12\,kg\) placed at \(x_2=4m\)
- \(m_3=30\,kg\) placed at \(x_3=2m\)
- \(m_4=6\,kg,\) placed at \(x_4=−6m.\)
Find the moment of the system with respect to the origin and find the center of mass of the system.
- Hint
-
Use the process from the previous example.
- Answer
-
\(M=24,\bar{x}=\dfrac{2}{5}m\)
We can generalize this concept to find the center of mass of a system of point masses in a plane. Let \(m_1\) be a point mass located at point \((x_1,y_1)\) in the plane. Then the moment \(M_x\) of the mass with respect to the \(x\)-axis is given by \(M_x=m_1y_1\). Similarly, the moment \(M_y\) with respect to the \(y\)-axis is given by
\[M_y=m_1x_1. \nonumber \]
Notice that the \(x\)-coordinate of the point is used to calculate the moment with respect to the \(y\)-axis, and vice versa. The reason is that the \(x\)-coordinate gives the distance from the point mass to the \(y\)-axis, and the \(y\)-coordinate gives the distance to the \(x\)-axis (see the following figure).

If we have several point masses in the \(xy\)-plane, we can use the moments with respect to the \(x\)- and \(y\)-axes to calculate the \(x\)- and \(y\)-coordinates of the center of mass of the system.
Let \(m_1\), \(m_2\), …, \(m_n\) be point masses located in the \(xy\)-plane at points \((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) respectively, and let \(\displaystyle m=\sum_{i=1}^nm_i\) denote the total mass of the system. Then the moments \(M_x\) and \(M_y\) of the system with respect to the \(x\)- and \(y\)-axes, respectively, are given by
\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]
and
\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]
Also, the coordinates of the center of mass \((\bar{x},\bar{y})\) of the system are
\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]
and
\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]
The next example demonstrates how to the center of mass formulas (Equations \ref{COM1} - \ref{COM4}) may be applied.
Suppose three point masses are placed in the \(xy\)-plane as follows (assume coordinates are given in meters):
- \(m_1=2\,kg\) placed at \((−1,3),\)
- \(m_2=6\,kg\) placed at \((1,1),\)
- \(m_3=4\,kg\) placed at \((2,−2).\)
Find the center of mass of the system.
Solution
First we calculate the total mass of the system:
\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]
Next we find the moments with respect to the \(x\)- and \(y\)-axes:
\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]
Then we have
\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]
and
\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]
The center of mass of the system is \((1,1/3),\) in meters.
Suppose three point masses are placed on a number line as follows (assume coordinates are given in meters):
- \(m_1=5\,kg,\) placed at \((−2,−3),\)
- \(m_2=3\, kg,\) placed at \((2,3),\)
- \(m_3=2\, kg,\) placed at \((−3,−2).\)
Find the center of mass of the system.
- Hint
-
Use the process from the previous example.
- Answer
-
\((−1,−1)\) m
Center of Mass of Thin Plates
So far we have looked at systems of point masses on a line and in a plane. Now, instead of having the mass of a system concentrated at discrete points, we want to look at systems in which the mass of the system is distributed continuously across a thin sheet of material. For our purposes, we assume the sheet is thin enough that it can be treated as if it is two-dimensional. Such a sheet is called a lamina. Next we develop techniques to find the center of mass of a lamina. In this section, we also assume the density of the lamina is constant.
Laminas are often represented by a two-dimensional region in a plane. The geometric center of such a region is called its centroid. Since we have assumed the density of the lamina is constant, the center of mass of the lamina depends only on the shape of the corresponding region in the plane; it does not depend on the density. In this case, the center of mass of the lamina corresponds to the centroid of the delineated region in the plane. As with systems of point masses, we need to find the total mass of the lamina, as well as the moments of the lamina with respect to the \(x\)- and \(y\)-axes.
We first consider a lamina in the shape of a rectangle. Recall that the center of mass of a lamina is the point where the lamina balances. For a rectangle, that point is both the horizontal and vertical center of the rectangle. Based on this understanding, it is clear that the center of mass of a rectangular lamina is the point where the diagonals intersect, which is a result of the symmetry principle, and it is stated here without proof.
If a region \(R\) is symmetric about a line \(l\), then the centroid of \(R\) lies on \(l\).
Let’s turn to more general laminas. Suppose we have a lamina bounded above by the graph of a continuous function \(f(x)\), below by the \(x\)-axis, and on the left and right by the lines \(x=a\) and \(x=b\), respectively, as shown in the following figure.
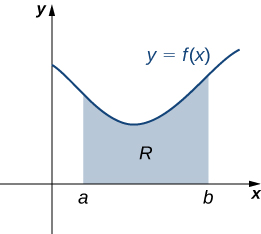
As with systems of point masses, to find the center of mass of the lamina, we need to find the total mass of the lamina, as well as the moments of the lamina with respect to the \(x\)- and \(y\)-axes. As we have done many times before, we approximate these quantities by partitioning the interval \([a,b]\) and constructing rectangles.
For \(i=0,1,2,…,n,\) let \(P={x_i}\) be a regular partition of \([a,b]\). Recall that we can choose any point within the interval \([x_{i−1},x_i]\) as our \(x^∗_i\). In this case, we want \(x^∗_i\) to be the x-coordinate of the centroid of our rectangles. Thus, for \(i=1,2,…,n\), we select \(x^∗_i∈[x_{i−1},x_i]\) such that \(x^∗_i\) is the midpoint of the interval. That is, \(x^∗_i=(x_{i−1}+x_i)/2\). Now, for \(i=1,2,…,n,\) construct a rectangle of height \(f(x^∗_i)\) on \([x_{i−1},x_i].\) The center of mass of this rectangle is \((x^∗_i,(f(x^∗_i))/2),\) as shown in the following figure.
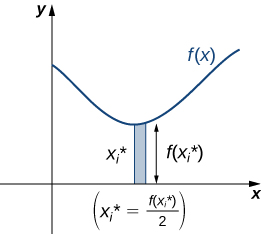
Next, we need to find the total mass of the rectangle. Let \(ρ\) represent the density of the lamina (note that \(ρ\) is a constant). In this case, \(ρ\) is expressed in terms of mass per unit area. Thus, to find the total mass of the rectangle, we multiply the area of the rectangle by \(ρ\). Then, the mass of the rectangle is given by \(ρf(x^∗_i)Δx\).
To get the approximate mass of the lamina, we add the masses of all the rectangles to get
\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]
Equation \ref{eq51} is a Riemann sum. Taking the limit as \(n→∞\) gives the exact mass of the lamina:
\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]
Next, we calculate the moment of the lamina with respect to the x-axis. Returning to the representative rectangle, recall its center of mass is \((x^∗_i,(f(x^∗_i))/2)\). Recall also that treating the rectangle as if it is a point mass located at the center of mass does not change the moment. Thus, the moment of the rectangle with respect to the x-axis is given by the mass of the rectangle, \(ρf(x^∗_i)Δx\), multiplied by the distance from the center of mass to the x-axis: \((f(x^∗_i))/2\). Therefore, the moment with respect to the x-axis of the rectangle is \(ρ([f(x^∗_i)]^2/2)Δx.\) Adding the moments of the rectangles and taking the limit of the resulting Riemann sum, we see that the moment of the lamina with respect to the x-axis is
\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]
We derive the moment with respect to the y-axis similarly, noting that the distance from the center of mass of the rectangle to the y-axis is \(x^∗_i\). Then the moment of the lamina with respect to the y-axis is given by
\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]
We find the coordinates of the center of mass by dividing the moments by the total mass to give \(\bar{x}=M_y/m\) and \(\bar{y}=M_x/m\). If we look closely at the expressions for \(M_x,M_y\), and \(m\), we notice that the constant \(ρ\) cancels out when \(\bar{x}\) and \(\bar{y}\) are calculated.
We summarize these findings in the following theorem.
Let R denote a region bounded above by the graph of a continuous function \(f(x)\), below by the x-axis, and on the left and right by the lines \(x=a\) and \(x=b\), respectively. Let \(ρ\) denote the density of the associated lamina. Then we can make the following statements:
- The mass of the lamina is \[m=ρ∫^b_af(x)dx. \label{eq4a} \]
- The moments \(M_x\) and \(M_y\) of the lamina with respect to the x- and y-axes, respectively, are \[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] and \[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
- The coordinates of the center of mass \((\bar{x},\bar{y})\) are \[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] and \[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]
In the next example, we use this theorem to find the center of mass of a lamina.
Let R be the region bounded above by the graph of the function \(f(x)=\sqrt{x}\) and below by the x-axis over the interval \([0,4]\). Find the centroid of the region.
Solution
The region is depicted in the following figure.
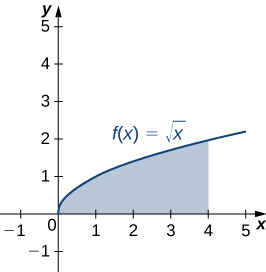
Since we are only asked for the centroid of the region, rather than the mass or moments of the associated lamina, we know the density constant \(ρ\) cancels out of the calculations eventually. Therefore, for the sake of convenience, let’s assume \(ρ=1\).
First, we need to calculate the total mass (Equation \ref{eq4a}):
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]
Next, we compute the moments (Equation \ref{eq4d}):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]
and (Equation \ref{eq4c}):
\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]
Thus, we have (Equation \ref{eq4d}):
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]
and (Equation \ref{eq4e}):
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]
The centroid of the region is \((12/5,3/4).\)
Let \(R\) be the region bounded above by the graph of the function \(f(x)=x^2\) and below by the x-axis over the interval \([0,2].\) Find the centroid of the region.
- Hint
-
Use the process from the previous example.
- Answer
-
The centroid of the region is \((3/2,6/5).\)
We can adapt this approach to find centroids of more complex regions as well. Suppose our region is bounded above by the graph of a continuous function \(f(x)\), as before, but now, instead of having the lower bound for the region be the x-axis, suppose the region is bounded below by the graph of a second continuous function, \(g(x)\), as shown in Figure \(\PageIndex{7}\).
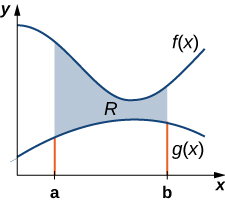
Again, we partition the interval \([a,b]\) and construct rectangles. A representative rectangle is shown in Figure \(\PageIndex{8}\).
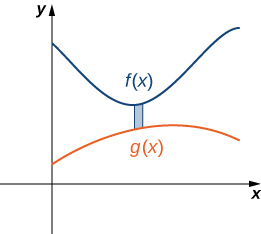
Note that the centroid of this rectangle is \((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). We won’t go through all the details of the Riemann sum development, but let’s look at some of the key steps. In the development of the formulas for the mass of the lamina and the moment with respect to the y-axis, the height of each rectangle is given by \(f(x^∗_i)−g(x^∗_i)\), which leads to the expression \(f(x)−g(x)\) in the integrands.
In the development of the formula for the moment with respect to the x-axis, the moment of each rectangle is found by multiplying the area of the rectangle, \(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) by the distance of the centroid from the \(x\)-axis, \((f(x^∗_i)+g(x^∗_i))/2\), which gives \(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). Summarizing these findings, we arrive at the following theorem.
Let \(R\) denote a region bounded above by the graph of a continuous function \(f(x),\) below by the graph of the continuous function \(g(x)\), and on the left and right by the lines \(x=a\) and \(x=b\), respectively. Let \(ρ\) denote the density of the associated lamina. Then we can make the following statements:
- The mass of the lamina is \[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
- The moments \(M_x\) and \(M_y\) of the lamina with respect to the x- and y-axes, respectively, are \[M_x=ρ∫^b_a\frac{1}{2}([f(x)]^2−[g(x)]^2)dx \nonumber \] and \[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
- The coordinates of the center of mass \(\bar{x},\bar{y})\) are \[\bar{x}=\dfrac{M_y}{m} \nonumber \] and \[\bar{y}=\dfrac{M_x}{m} \nonumber \]
We illustrate this theorem in the following example.
Let R be the region bounded above by the graph of the function \(f(x)=1−x^2\) and below by the graph of the function \(g(x)=x−1.\) Find the centroid of the region.
Solution
The region is depicted in the following figure.
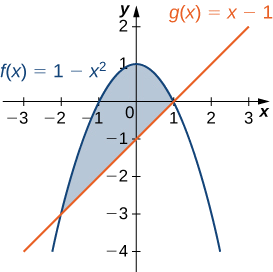
The graphs of the functions intersect at \((−2,−3)\) and \((1,0)\), so we integrate from −2 to 1. Once again, for the sake of convenience, assume \(ρ=1\).
First, we need to calculate the total mass:
\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]
Next, we compute the moments:
\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]
and
\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]
Therefore, we have
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]
and
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]
The centroid of the region is \((−(1/2),−(3/5)).\)
Let \(R\) be the region bounded above by the graph of the function \(f(x)=6−x^2\) and below by the graph of the function \(g(x)=3−2x.\) Find the centroid of the region.
- Hint
-
Use the process from the previous example.
- Answer
-
The centroid of the region is \((1,13/5).\)
The Symmetry Principle
We stated the symmetry principle earlier, when we were looking at the centroid of a rectangle. The symmetry principle can be a great help when finding centroids of regions that are symmetric. Consider the following example.
Let R be the region bounded above by the graph of the function \(f(x)=4−x^2\) and below by the x-axis. Find the centroid of the region.
Solution
The region is depicted in the following figure
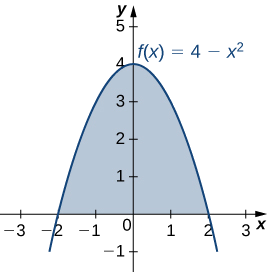
The region is symmetric with respect to the y-axis. Therefore, the x-coordinate of the centroid is zero. We need only calculate \(\bar{y}\). Once again, for the sake of convenience, assume \(ρ=1\).
First, we calculate the total mass:
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]
Next, we calculate the moments. We only need \(M_x\):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]
Then we have
\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]
The centroid of the region is \((0,8/5).\)
Let \(R\) be the region bounded above by the graph of the function \(f(x)=1−x^2\) and below by \(x\)-axis. Find the centroid of the region.
- Hint
-
Use the process from the previous example.
- Answer
-
The centroid of the region is \((0,2/5).\)
The Grand Canyon Skywalk opened to the public on March 28, 2007. This engineering marvel is a horseshoe-shaped observation platform suspended 4000 ft above the Colorado River on the West Rim of the Grand Canyon. Its crystal-clear glass floor allows stunning views of the canyon below (see the following figure).

The Skywalk is a cantilever design, meaning that the observation platform extends over the rim of the canyon, with no visible means of support below it. Despite the lack of visible support posts or struts, cantilever structures are engineered to be very stable and the Skywalk is no exception. The observation platform is attached firmly to support posts that extend 46 ft down into bedrock. The structure was built to withstand 100-mph winds and an 8.0-magnitude earthquake within 50 mi, and is capable of supporting more than 70,000,000 lb.
One factor affecting the stability of the Skywalk is the center of gravity of the structure. We are going to calculate the center of gravity of the Skywalk, and examine how the center of gravity changes when tourists walk out onto the observation platform.
The observation platform is U-shaped. The legs of the U are 10 ft wide and begin on land, under the visitors’ center, 48 ft from the edge of the canyon. The platform extends 70 ft over the edge of the canyon.
To calculate the center of mass of the structure, we treat it as a lamina and use a two-dimensional region in the xy-plane to represent the platform. We begin by dividing the region into three subregions so we can consider each subregion separately. The first region, denoted \(R_1\), consists of the curved part of the U. We model \(R_1\) as a semicircular annulus, with inner radius 25 ft and outer radius 35 ft, centered at the origin (Figure \(\PageIndex{12}\)).
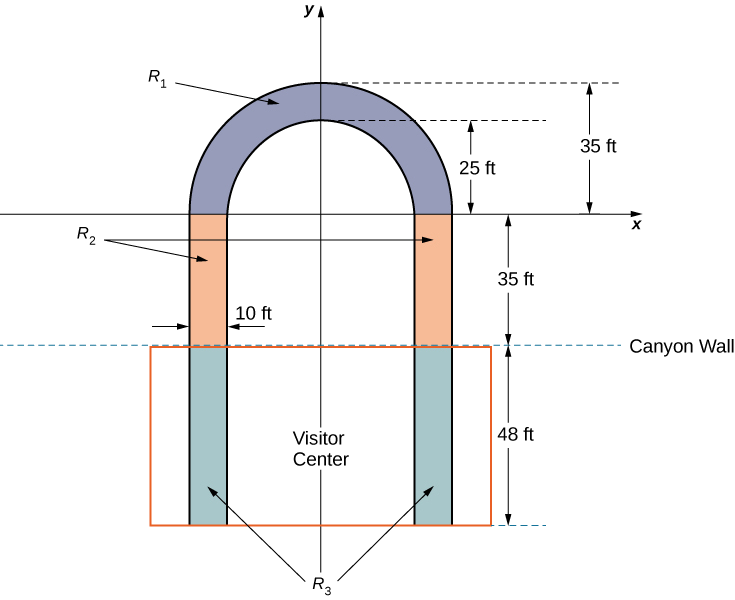
The legs of the platform, extending 35 ft between \(R_1\) and the canyon wall, comprise the second sub-region, \(R_2\). Last, the ends of the legs, which extend 48 ft under the visitor center, comprise the third sub-region, \(R_3\). Assume the density of the lamina is constant and assume the total weight of the platform is 1,200,000 lb (not including the weight of the visitor center; we will consider that later). Use \(g=32\;ft/sec^2\).
- Compute the area of each of the three sub-regions. Note that the areas of regions \(R_2\) and \(R_3\) should include the areas of the legs only, not the open space between them. Round answers to the nearest square foot.
- Determine the mass associated with each of the three sub-regions.
- Calculate the center of mass of each of the three sub-regions.
- Now, treat each of the three sub-regions as a point mass located at the center of mass of the corresponding sub-region. Using this representation, calculate the center of mass of the entire platform.
- Assume the visitor center weighs 2,200,000 lb, with a center of mass corresponding to the center of mass of \(R_3\).Treating the visitor center as a point mass, recalculate the center of mass of the system. How does the center of mass change?
- Although the Skywalk was built to limit the number of people on the observation platform to 120, the platform is capable of supporting up to 800 people weighing 200 lb each. If all 800 people were allowed on the platform, and all of them went to the farthest end of the platform, how would the center of gravity of the system be affected? (Include the visitor center in the calculations and represent the people by a point mass located at the farthest edge of the platform, 70 ft from the canyon wall.)
Theorem of Pappus
This section ends with a discussion of the theorem of Pappus for volume, which allows us to find the volume of particular kinds of solids by using the centroid. (There is also a theorem of Pappus for surface area, but it is much less useful than the theorem for volume.)
Let \(R\) be a region in the plane and let l be a line in the plane that does not intersect \(R\). Then the volume of the solid of revolution formed by revolving \(R\) around l is equal to the area of \(R\) multiplied by the distance d traveled by the centroid of \(R\).
We can prove the case when the region is bounded above by the graph of a function \(f(x)\) and below by the graph of a function \(g(x)\) over an interval \([a,b]\), and for which the axis of revolution is the \(y\)-axis. In this case, the area of the region is \(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Since the axis of rotation is the \(y\)-axis, the distance traveled by the centroid of the region depends only on the \(x\)-coordinate of the centroid, \(\bar{x}\), which is
\[x=\dfrac{M_y}{m}, \nonumber \]
where
\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]
and
\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Then,
\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]
and thus
\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
However, using the method of cylindrical shells, we have
\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
So,
\[V=d⋅A \nonumber \]
and the proof is complete.
□
Let \(R\) be a circle of radius 2 centered at \((4,0).\) Use the theorem of Pappus for volume to find the volume of the torus generated by revolving \(R\) around the \(y\)-axis.
Solution
The region and torus are depicted in the following figure.
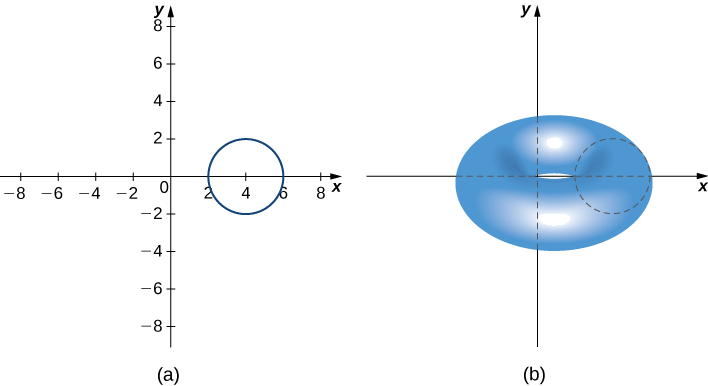
The region \(R\) is a circle of radius 2, so the area of R is \(A=4π\;\text{units}^2\). By the symmetry principle, the centroid of R is the center of the circle. The centroid travels around the \(y\)-axis in a circular path of radius 4, so the centroid travels \(d=8π\) units. Then, the volume of the torus is \(A⋅d=32π^2\) units3.
Let R be a circle of radius 1 centered at \((3,0).\) Use the theorem of Pappus for volume to find the volume of the torus generated by revolving R around the \(y\)-axis.
- Hint
-
Use the process from the previous example.
- Answer
-
\(6π^2\) units3
Key Concepts
- Mathematically, the center of mass of a system is the point at which the total mass of the system could be concentrated without changing the moment. Loosely speaking, the center of mass can be thought of as the balancing point of the system.
- For point masses distributed along a number line, the moment of the system with respect to the origin is \(\displaystyle M=\sum^n_{i=1}m_ix_i.\) For point masses distributed in a plane, the moments of the system with respect to the \(x\)- and \(y\)-axes, respectively, are \(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) and \(\displaystyle M_y=\sum^n_{i=}m_ix_i\), respectively.
- For a lamina bounded above by a function \(f(x)\), the moments of the system with respect to the \(x\)- and \(y\)-axes, respectively, are \(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) and \(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
- The \(x\)- and \(y\)-coordinates of the center of mass can be found by dividing the moments around the \(y\)-axis and around the \(x\)-axis, respectively, by the total mass. The symmetry principle says that if a region is symmetric with respect to a line, then the centroid of the region lies on the line.
- The theorem of Pappus for volume says that if a region is revolved around an external axis, the volume of the resulting solid is equal to the area of the region multiplied by the distance traveled by the centroid of the region.
Key Equations
- Mass of a lamina
\(\displaystyle m=ρ∫^b_af(x)dx\)
- Moments of a lamina
\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)
- Center of mass of a lamina
\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)
Glossary
- center of mass
- the point at which the total mass of the system could be concentrated without changing the moment
- centroid
- the centroid of a region is the geometric center of the region; laminas are often represented by regions in the plane; if the lamina has a constant density, the center of mass of the lamina depends only on the shape of the corresponding planar region; in this case, the center of mass of the lamina corresponds to the centroid of the representative region
- lamina
- a thin sheet of material; laminas are thin enough that, for mathematical purposes, they can be treated as if they are two-dimensional
- moment
- if n masses are arranged on a number line, the moment of the system with respect to the origin is given by \(\displaystyle M=\sum^n_{i=1}m_ix_i\); if, instead, we consider a region in the plane, bounded above by a function \(f(x)\) over an interval \([a,b]\), then the moments of the region with respect to the \(x\)- and \(y\)-axes are given by \(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) and \(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), respectively
- symmetry principle
- the symmetry principle states that if a region \(R\) is symmetric about a line \(I\), then the centroid of \(R\) lies on \(I\)
- theorem of Pappus for volume
- this theorem states that the volume of a solid of revolution formed by revolving a region around an external axis is equal to the area of the region multiplied by the distance traveled by the centroid of the region

