5.1: Solving Equations Part I
- Page ID
- 137921
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall that a variable is a symbol (usually a letter) that stands for a value that varies. If a variable in an equation is replaced by a number and a true statement results, then that number is called a solution of the equation.
Example 1
Is −6 a solution of the equation 2x + 5= −7?
Solution
Substitute −6 for x in the equation.
\[ \begin{aligned} 2x + 5 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 2(-6)+5 = -7 ~ & \textcolor{red}{ \text{ Substitute } -6 \text{ for } x.} \\ -12 + 5 = -7 ~ & \textcolor{red}{ \text{ On the left, multiply first.}} \\ -7 = -7 ~ & \textcolor{red}{ \text{ On the left, add.}} \end{aligned}\nonumber \]
Because the last statement is a true statement, −6 is a solution of the equation.
Exercise
Is −4 a solution of 8 − 2x = 5?
- Answer
-
No
Adding or Subtracting the Same Amount
Two equations having the same set of solutions are equivalent. For example, 2x+5 = −7 and x = −6 have the same solutions. Therefore, they are equivalent equations. Certain algebraic operations produce equivalent equations.
Producing Equivalent Equations
Adding the Same Quantity to Both Sides of an Equation. If we start with the equation
\[a = b,\nonumber \]
then adding c to both sides of the equation produces the equivalent equation
\[ a + c = b + c.\nonumber \]
Subtracting the Same Quantity from Both Sides of an Equation. If we start with the equation
\[a = b,\nonumber \]
then subtracting c from both sides of the equation produces the equivalent equation
\[a − c = b − c.\nonumber \]
That is, adding or subtracting the same amount from both sides of an equation will not change the solutions of the equation.
Example 2
Solve for x:
x + 3= −7
Solution
To undo the effect of adding 3, subtract 3 from both sides of the equation.
\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + 3 - 3 = -7 -3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ x = -7 + (-3) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify the left hand side. On the right,}} \\ \textcolor{red}{ \text{ express subtractions as adding the opposite.}} \end{array} \\ x = -10 \end{aligned}\nonumber \]
To check the solution, substitute −10 for x in the original equation and simplify.
\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -10 + 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ =7 = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Since the last line of the check is a true statement, this confirms that −10 is a solution.
Exercise
Solve for x:
x + 9 = -11
- Answer
-
x = −20
Example 3
Solve for x:
x − 8 = −11
Solution
To undo the effect of subtracting 8, add 8 to both sides of the equation.
\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - 8 + 8 = -11+ 8 ~ & \textcolor{red}{ \text{ Add 8 to both sides.}} \\ x = -3 ~ & \textcolor{red}{ \text{ Simplify both equations.}} \end{aligned}\nonumber \]
To check the solution, substitute −3 for x in the original equation and simplify.
\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3 - 8 = -11 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x.} \\ -11 = -11 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Since the last line of the check is a true statement, this confirms that −3 is a solution.
Exercise
Solve for x:
x − 2 = −7
- Answer
-
x = −5
Sometimes a bit of simplification is in order before you start the solution process.
Example 4
Solve for y:
−8 + 2 = y − 11(−4)
Solution
First, simplify both sides of the equation.
\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -6 = y -(-44) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify. On the left, } -8 + 2 = -6.} \\ \textcolor{red}{ \text{ On the right, } 11(-4) = -44.} \end{array} \\ -6 = y + 44 - 44 ~ & \textcolor{red}{ \text{ Subtract 44 from both sides of the equation.}} \\ -6 + (-44) = y ~ & \textcolor{red}{ \text{ Express subtraction as addition. Simplify on the right.}} \\ -50 = y \end{aligned}\nonumber \]
To check the solution, substitute −50 for y in the original equation and simplify.
\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -8 + 2 = -50 -11 (-4) ~ & \textcolor{red}{ \text{ Substitute } -50 \text{ for } y.} \\ -6 = -50 -(-44) ~ & \textcolor{red}{ \text{ Express subtraction on the right as addition.}} \\ -6 = -6 ~ & \textcolor{red}{ \text{ On the right, add: } -50 + 44 = -6.} \end{aligned}\nonumber \]
Since the last line of the check is a true statement, this confirms that −50 is a solution.
Exercise
Solve for y:
y + 2(−4) = −8 + 6
- Answer
-
y = 6
Multiplying or Dividing by the Same Amount
Adding and subtracting is not the only way to produce an equivalent equation.
Producing Equivalent Equations
Multiplying Both Sides of an Equation by the Same Quantity. If we start with the equation
\[a = b,\nonumber \]
then multiplying both sides of the equation by c produces the equivalent equation
\[ a \cdot c = b \cdot c, \text{ or equivalently, } ac = bc,\nonumber \]
provided c ≠ 0.
Dividing Both Sides of an Equation by the Same Quantity. If we start with the equation
\[ a = b,\nonumber \]
then dividing both sides of the equation by c produces the equivalent equation
\[ \frac{a}{c} = \frac{b}{c},\nonumber \]
provided c ≠ 0.
That is, multiplying or dividing both sides of an equation by the same amount will not change the solutions of the equation.
Example 5
Solve for x:
−3x = 30
Solution
To undo the effect of multiplying by −3, divide both sides of the equation by −3.
\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-3x}{-3} = \frac{30}{-3} ~ & \textcolor{red}{ \text{ Divide both sides by }-3.} \\ x = -10 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } -3 \text{ times } x, \text{ divided by } -3 \text{ is } x.} \\ \textcolor{red}{ \text{ On the right, } 30/(-3)=-10.} \end{array} \end{aligned}\nonumber \]
To check the solution, substitute −10 for x in the original equation and simplify.
\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3(-10) = 30 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ 30 - 30 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Because the last line of the check is a true statement, this confirms that −10 is a solution.
Exercise
Solve for z:
−4z = −28
- Answer
-
z = 7
Example 6
Solve for x:
\( \frac{x}{-2} = -20\)
Solution
To undo the effect of dividing by −2, multiply both sides of the equation by −2.
\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -2 \left( \frac{x}{-2} \right) - -2 (-20) ~ & \textcolor{red}{ \text{ Multiply both sides by } -2.} \\ x = 40 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } x \text{ divided by } -2, \text{ multiplied by } -2,} \\ \textcolor{red}{ \text{ the result is } x. \text{ On the right, } -2(-20) = 40.} \end{array} \end{aligned}\nonumber \]
To check the solution, substitute 40 for x in the original equation and simplify.
\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{40}{-2} = -20 ~ & \textcolor{red}{ \text{ Substitute 40 for } x.} \\ -20 = -20 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Because the last line of the check is a true statement, this confirms that 40 is a solution.
Combining Operations
Consider wrapping and unwrapping a present. To wrap a present we: (1) put the gift paper on, (2) put the tape on, and (3) put the decorative bow on. To unwrap the gift, we must “undo” each of these steps in inverse order. Hence, to unwrap the gift we: (1) take off the decorative bow, (2) take off the tape, and (3) take off the gift paper.
Now, imagine a machine that takes its input, then: (1) multiplies the input by 2, and (2) adds 3 to the result. This machine is pictured on the left in Figure 2.16.
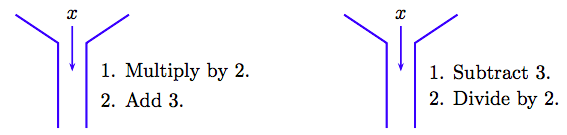
To “unwrap” the effect of the machine on the left, we need a machine that will “undo” each of the steps of the first machine, but in inverse order. The “unwrapping” machine is pictured on the right in Figure 2.16. It will first subtract three from its input, then divide the result by 2. Note that each of these operations “undoes” the corresponding operation of the first machine, but in inverse order.
For example, drop the integer 7 into the first machine on the left in Figure 2.16. First, we double 7, then add 3 to the result. The result is 2(7) + 3 = 17.
Now, to “unwrap” this result, we drop 17 into the second machine. We first subtract 3, then divide by 2. The result is (17 − 3)/2 = 7, the original integer input into the first machine.
Now, consider the equation
\[2x +3=7.\nonumber \]
On the left, order of operations demands that we first multiply x by 2, then add 3. To solve this equation for x, we must “undo” each of these operations in inverse order. Thus, we will (1) subtract three from both sides of the equation, then (2) divide both sides of the resulting equation by 2.
\[ \begin{aligned} 2x + 3 - 3 = 7 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = 4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2x}{2} = \frac{4}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Readers should check this solution in the original equation.
Example 7
Solve for x:
\(\frac{x}{4} - 3 = -7\)
Solution
On the left, order of operations demands that we first divide x by 4, then subtract 3. To solve this equation for x, we must “undo” each of these operations in inverse order. Thus, we will (1) add 3 to both sides of the equation, then (2) multiply both sides of the resulting equation by 4.
\[ \begin{aligned} \frac{x}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{x}{4} - 3 + 3 = -7 + 3 ~ & \textcolor{red}{ \text{ Add 3 to both sides.}} \\ \frac{x}{4} = -4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ 4 \left( \frac{x}{4} \right) = 4 (-4) ~ & \textcolor{red}{ \text{ Multiply both sides by 4.}} \\ x = -16 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Check
Substitute −16 for x in the original equation.
\[ \begin{aligned} \frac{x}{4} - 3 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-16}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -16 \text{ for } x.} \\ -4 -3 = -7 ~ & \textcolor{red}{ \text{ Divide first: } -16/4 = -4.} \\ -7 = - 7 ~ & \textcolor{red}{ \text{ Subtract: } -4 -3 = -7.} \end{aligned}\nonumber \]
Because the last line of the check is a true statement, −16 is a solution of the original equation.
Exercise
Solve for x:
\[ \frac{x}{2} + 6 = 4\nonumber \]
- Answer
-
x = -4
Example 8
Solve for t:
0 = 8 − 2t
Solution
On the right, order of operations demands that we first multiply t by −2, then add 8. To solve this equation for t, we must “undo” each of these operations in inverse order. Thus, we will (1) subtract 8 from both sides of the equation, then (2) divide both sides of the resulting equation by −2.
\[ \begin{aligned} 0 = 8 -2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 - 8 = 8 - 2t - 8 ~ & \textcolor{red}{ \text{ Subtract 8 from both sides.}} \\ -8 = -2t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{-8}{-2} = \frac{-2t}{-2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 4 = t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Check
Substitute 4 for t in the original equation.
\[ \begin{aligned} 0 = 8 - 2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 = 8 - 2(4) ~ & \textcolor{red}{ \text{ Substitute 4 for } t.} \\ 0 = 8-8 ~ & \textcolor{red}{ \text{ Multiply first: 2(4) = 8.}} \\ 0 = 0 ~ & \textcolor{red}{ \text{ Subtract: } 8-8=0.} \end{aligned}\nonumber \]
Because the last line in the check is a true statement, 4 is a solution of the original equation.
Exercise
Solve for r:
0 = 9 + 3r
- Answer
-
r = -3
Example 9
Solve for p:
\(-12 + 3 = -8+4 + \frac{p}{-3}.\)
Solution
Always simplify when possible.
\[ \begin{aligned} -12+3= -8+4+ \frac{p}{-3} ~ & \textcolor{red}{ \text{ Origianl equation.}} \\ -9 = -4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
On the right, order of operations demands that we first divide p by −3, then add −4. To solve this equation for p, we must “undo” each of these operations in inverse order. Thus, we will (1) add a positive 4 to both sides of the equation, then (2) multiply both sides of the resulting equation by −3.
\[ \begin{aligned} -9+-4 = -4+ \frac{p}{-3} + 4~ & \textcolor{red}{ \text{ Add 4 to both sides.}} \\ -5 = \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ -3(-5) = -3 \left( \frac{p}{-3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -3.} \\ 15 = p ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Check
Substitute 15 for p in the original equation.
\[ \begin{aligned} -12 + 3 = =8 + 4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ -12 + 3 = -8 + 4 + \frac{15}{-3} ~ & \textcolor{red}{ \text{ Substitute 15 for } p.} \\ -9 = -8 + 4 + (-5) ~ & \begin{aligned} \textcolor{red}{ \text{ On the left, add: } -12 + 3 = -9. \text{ On the }} \\ \textcolor{red}{ \text{ right, divide: } 15/(-3) = -5.} \end{aligned} \\ -9 = -4 + (-5) ~ & \textcolor{red}{ \text{ On the right, } -8 + 4 = -4.} \\ -9 = -9 ~ & \textcolor{red}{ \text{ On the right, add: } -4 + (-5) = -9.} \end{aligned}\nonumber \]
Because the last line in the check is a true statement, 15 is a solution of the original equation.
Exercise
Solve for q:
\[ \frac{q}{-2} -9 = -8+3\nonumber \]
- Answer
-
q = −8
Applications
Let’s look at some applications of equations involving integers. First, we remind readers that a solution of a word problem must incorporate each of the following steps.
Requirements for Word Problem Solutions
- Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation. Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation. You must always solve the equation set up in the previous step.
- Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units.
- Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
Example 10
A student’s bank account is overdrawn. After making a his account, Allen finds that he is overdrawn by $15. What was his account balance before his withdrawal? deposit of $120, he finds that his account is still overdrawn by an amount of $75. What was his balance before he made his deposit?
Solution
In our solution, we address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. In this case, the unknown is the original balance in the student’s account. Let B represent this original balance.
2. Set up an Equation. A positive integer represents a healthy balance, while a negative number represents an account that is overdrawn. After the student’s deposit, the account is still overdrawn by $75. We will say that this balance is −$75. Thus,
\[ \begin{array}{c c c c c} \colorbox{cyan}{Original Balance} & \text{plus} & \colorbox{cyan}{Student Deposit} & \text{equals} & \colorbox{cyan}{Current Balance} \\ B & + & $120 & = & -$75 \end{array}\nonumber \]
3. Solve the Equation. To “undo” the addition, subtract 120 from both sides of the equation.
\[ \begin{aligned} B + 120 = -75 ~ & \textcolor{red}{ \text{ Original equation.}} \\ B + 120 - 120 = -75 - 120 ~ & \textcolor{red}{ \text{ Subtract 120 from both sides.}} \\ B = -195 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Answer the Question. The original balance was overdrawn to the tune of $195.
5. Look Back. If the original balance was overdrawn by $195, then we let −$195 represent this balance. The student makes a deposit of $120. Add this to the original balance to get −$195 + $120 = −$75, the correct current balance.
Exercise
After withdrawing $125 from his account, Allen finds that he is overdrawn by $15. What was his account balance before his withdrawal?
- Answer
-
$110
Example 11
Three more than twice a certain number is −11. Find the unknown number.
Solution
In our solution, we address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. Let x represent the unknown number. 2. Set up an Equation. “Three more than twice a certain number” becomes:
\[ \begin{array}{c c c c c} \colorbox{cyan}{Three} & \text{more than} & \colorbox{cyan}{Twice a Certain Number} & \text{is} & \colorbox{cyan}{-11} \\ 3 & + & 2x & = & 11 \end{array}\nonumber \]
3. Solve the Equation. On the left, order of operations requires that we first multiply x by 2, then add 3. To solve this equation for x, we must “undo” each of these operations in inverse order. Thus, we will (1) subtract 3 from both sides of the equation, then (2) divide both sides of the resulting equation by 2.
\[ \begin{aligned} 3 + 2x = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 + 2x - 3 = -11 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = -14 ~ & \textcolor{red}{ \text{ Simplify both sides.}} ~ \\ \frac{2x}{2} = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Answer the Question. The unknown number is −7.
5. Look Back. Does the answer satisfy the problem constraints? Three more than twice −7 is three more than −14, or −11. So the solution is correct.
Exercise \(\PageIndex{1}\)
Five less than twice a certain number is −7. Find the unknown number.
- Answer
-
−1
Exercises
3. Is 6 a solution of 3x + 1 = 19?
5. Is -3 a solution of 4x +5= −8?
11. Is −6 a solution of −2x + 3 = 15?
In Exercises 13-28, solve the given equation for x.
13. x − 13 = 11
15. x − 3 = 6
17. x + 10 = 17
19. x − 6 = 1
21. x − 15 = −12
23. x + 11 = −19
25. x +2 = 1
27. x + 5= −5
Solve the given equation for x.
29. −x = −20
31. \(\frac{x}{−7}\) = 10
35. \(\frac{x}{9}\) = −16
37. −10x = 20
41. −2x = 28
44. \(\frac{x}{−8}\) = −1
49. 5x − 14 = −79
51. −10x − 16 = 24
53. 9x +5 = −85
57. −x + 8 = 13
59. 12x − 15 = −3
63. 19x + 18 = 113
65. −14x + 12 = −2
69. Two less than eight times an unknown number is −74. Find the unknown number.
71. Eight more than two times an unknown number is 0. Find the unknown number.
73. The number −6 is 2 more than an unknown number. Find the unknown number.
75. Three more than eight times an unknown number is −29. Find the unknown number.
79. The quotient of two integers is 5. One of the integers is −2. Find the other integer.
85. A student’s bank account is overdrawn. After making a deposit of $260, he finds that his account is still overdrawn by an amount of $70. What was his balance before he made his deposit?
87. A student’s bank account is overdrawn. After making a deposit of $360, he finds that his account is still overdrawn by an amount of $90. What was his balance before he made his deposit?
92. The number −16 is 4 times larger than an unknown number. Find the unknown number.
93. Two less than nine times an unknown number is 7. Find the unknown number.
Answers
3. Yes
5. No
11. Yes
13. 24
15. 9
17. 7
19. 7
21. 3
23. −30
25. −1
27. −10
29. 20
31. −70
35. −144
37. −2
41. −14
44. 8
49. −13
51. −4
53. −10
57. −5
59. 1
63. 5
65. 1
69. −9
71. −4
73. −8
75. −4
79. −10
85. −$330
87. −$450
92. −4
93. 1