9.3: General Applications of Percent
- Page ID
- 137939
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we will look at an assortment of practical problems involving percent.
Example 1
Myrna notes that 20% of her class is absent. If the class has 45 students, how many students are absent?
Solution
Let n represent the number of students that are absent. Then we can translate the problem statement into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Number absent} & \text{ is } & \colorbox{cyan}{20%} & \text{ of } & \colorbox{cyan}{total number of students in the class} \\ n & = & 20 \% & \cdot & 45 \end{array}\nonumber \]
Because 20% = 0.20,
\[ \begin{aligned} n = 0.20 \cdot 45 ~ & \textcolor{red}{20% = 0.20} \\ n = 9 ~ & \textcolor{red}{ \text{ Multiply: } 0.20 \cdot 45 = 9.} \end{aligned}\nonumber \]
Therefore, 9 students are absent.
Exercise
Aaron notes that 15% of his class is absent. If the class has 80 students, how many students are absent?
- Answer
-
12
Example 2
Misty answered 90% of the questions on her mathematics examination correctly. If Misty had 27 correct answers, how many questions were on the exam?
Solution
Let N represent the number of questions on the examination.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Number of correct answers} & \text{ is } & \colorbox{cyan}{90%} & \text{ of } & \colorbox{cyan}{total number of questions} \\ 27 & = & 90 \% & \cdot & N \end{array}\nonumber \]
Because 90% = 0.90, this last equation can be written as
\[27 = 0.90N.\nonumber \]
Solve for N.
\[ \begin{aligned} \frac{27}{0.90} = \frac{0.90N}{0.90} ~ & \textcolor{red}{ \text{ Divide both sides by 0.90.}} \\ 30 = N ~ & \textcolor{red}{ \text{ Divide: 27/0.90 = 30.}} \end{aligned}\nonumber \]
Hence, there were 30 questions on the examination.
Exercise
Erin asnwered 85% of the questions on her english examination correctly. If she had 34 correct answers, how many questions were on her exam?
- Answer
-
40
Example 3
Misty answered 30 of 40 possible questions on her sociology examination correctly. What percent of the total number of questions did Misty mark correctly?
Solution
Let p represent the percent of the total number of questions marked correctly. Then we can translate the problem statement into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Number of correct answers} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{total number of questions} \\ 30 & = & p & \cdot & 40 \end{array}\nonumber \]
Because multiplication is commutative, we can write the last equation in the form
\[30 = 40p.\nonumber \]
Solve for p.
\[ \begin{aligned} \frac{30}{40} = \frac{40p}{40} ~ & \textcolor{red}{ \text{ Divide both sides by 40.}} \\ \frac{3}{4} = p ~ & \textcolor{red}{ \text{ Reduce: 30/40 = 3/4.}} \end{aligned}\nonumber \]
We need to change p = 3/4 to a percent. There are two ways to do this:
- We can divide 3 by 4 to get
\[ \begin{aligned} p = \frac{3}{4} ~ \\ = 0.75 ~ & \textcolor{red}{ \text{ Divide: 3/4=0.75.}} \\ = 75 \% ~ & \textcolor{red}{ \text{ Move decimal point 2 places right.}} \end{aligned}\nonumber \]
- We can create an equivalent fraction with a denominator of 100; i.e.,
\[ \begin{aligned} p = \frac{3}{4} ~ \\ = \frac{3 \cdot \textcolor{red}{25}}{4 \cdot \textcolor{red}{25}} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 25.}} \\ = \frac{75}{100} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = 75 \%. ~ & \textcolor{red}{ \text{ Percent means parts per hundred.}} \end{aligned}\nonumber \]
Either way, Misty got 75% of the questions on her sociology examination correct.
Exercise
Alphonso answered 19 of 25 questions on his biology test correctly. What percent of the questions did he mark correctly?
- Answer
-
76%
Example 4
35 millilitres of a 60 millilitre solution is hydrochloric acid. What percent of the solution is hydrochloric acid?
Solution
Let p represent the percent of the percent of the solution that is hydrochloric acid. Then we can translate the problem statement into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Amount of hydrochloric acid} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{the tota amount of solution} \\ 35 & = & p & \cdot & 60 \end{array}\nonumber \]
Because multiplication is commutative, we can write the right-hand side of the last equation as follows.
\[35 = 60p\nonumber \]
Now we can solve for p.
\[ \begin{aligned} \frac{35}{60} = \frac{60p}{60} ~ & \textcolor{red}{ \text{ Divide both sides by 60.}} \\ \frac{7}{12} = p ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator by 5.}} \end{aligned}\nonumber \]
Now we must change p to a percent. We can do this exactly by creating an equivalent fraction with a denominator of 100.
\[ \frac{7}{12} = \frac{n}{100}\nonumber \]
Solve for n.
\[ \begin{aligned} 12n = 700 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ \frac{12n}{12} = \frac{700}{12} ~ & \textcolor{red}{ \text{ Divide both sides by 12.}} \\ n = \frac{175}{3} ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator by 4.}} \\ n = 58 \frac{1}{3} ~ & \textcolor{red}{ \text{ Change improper to mixed fraction.}} \end{aligned}\nonumber \]
Hence,
\[p = \frac{7}{12} = \frac{58 \frac{1}{3}}{100} = 58 \frac{1}{3} \%.\nonumber \]
Thus, \(58 \frac{1}{3} \%\) of the solution is hydrochloric acid.
Approximate Solution
If all that is needed is an approximate answer, say correct to the nearest tenth of a percent, then we would take a different approach starting with the line from above that has
\[\frac{35}{60} = p.\nonumber \]
We would divide 35 by 60 to get
\[p \approx 0.5833.\nonumber \]
Move the decimal two places to the right and append a percent symbol.

Round to the nearest tenth of a percent.
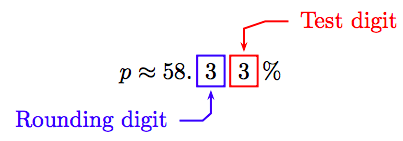
Because the test digit is less than 5, leave the rounding digit alone and truncate. Thus, correct to the nearest tenth of a percent,
\[p \approx 58.3 \%.\nonumber \]
Note that p ≈ 58.3% is approximate, but \(p = 58 \frac{1}{3} \%\) is exact.
Exercise
25 millilitres of a 40 millilitre solution is sulfuric acid. What percent of the solution is sulfuric acid?
- Answer
-
62.5%
Exercises
1. 31 millilitres of a 250 millilitre solution is sulphuric acid. What percent of the solution is sulphuric acid? Round your answer to the nearest tenth of a percent.
2. A family has completed 186 miles of a planned 346 mile trip. Find the percentage of the planned trip already traveled. Round your answer to the nearest percent.
3. Erin takes roll in her fifth grade class and finds that 19 out of 34 total students on her roster are present. Find the percentage of the class that is present, correct to the nearest percent.
4. A family has traveled 114 miles of a planned trip. This is 37% of the total distance they must travel on the trip. Find, correct to the nearest mile, the total distance they will travel on their trip.
5. Tami answered 70% of the questions on the physics examination correctly. If Tami had 98 correct answers, how many questions were on the exam?
6. A state charges 8% sales tax on all sales. If the sales tax on a computer is $20, find the sales price of the computer, correct to the nearest dollar.
7. Kenon earns 6% commission all his sales. If the sale of a computer earns him a $37 commission, find the sales price of the computer, correct to the nearest dollar.
8. A 23% nitric acid solution contains 59 millilitres of nitric acid. How many total millilitres of solution are present? Round your answer to the nearest millilitre.
9. In a state, a television sold for $428 is assessed a sales tax of $45. Find the sales tax rate, rounded to the nearest tenth of a percent.
10. Mars gravity. The force of gravity on Mars is only 38% of the force of gravity on earth. If you weigh 150 pounds on earth, how much will you weigh on Mars?
11. Seniors. 13% of Humboldt County’s population is age 65 and older, about 2% more than the state’s average. If the population of Humboldt County is approximately 130,000, how many people in Humboldt County are age 65 and older? Times-Standard 6/10/2009
12. Grow faster. “Approximately 28 million pounds of antibiotics were fed to farm animals in the US during 2008. Thirteen percent of that was fed to healthy animals to make them grow faster.” How many pounds of antibiotics were fed to healthy animals? Associated Press-Times-Standard 12/29/09 Pressure rises to stop antibiotics in agriculture.
13. Water supply. A new water desalination plant, the largest in the Western hemisphere, could come online by 2012 in Carlsbad, California, providing 50 million gallons of drinking water per day, or 10% of the supply for San Diego County. What is the total amount of drinking water supplied to San Diego County daily? Associated Press-Times-Standard
14. Reduce. Each year, Americans throw out an average of about 1, 600 pounds of waste per person. Arcata, CA resident Michael Winkler only uses one trash bag every year – totaling at most 40 pounds. Find the percent of average annual waste per person Mr. Winkler throws out to a tenth of a percent. Times-Standard Allison White 12/26/09 Waste not...
Answers
1. 12.4
2. 54
3. 56
4. 308 mi
5. 140
6. $250
7. $617
8. 257 ml
9. 10.5
10. 57 pounds
11. 16,900
12. 3.84 million pounds
13. 500 million gallons
14. Mr. Winkler throws out 2.5% of the average American’s waste.


