6.E: Applications of Integration (Exercises)
- Page ID
- 3438
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
These are homework exercises to accompany OpenStax's "Calculus" Textmap.
6.1: Areas between Curves
For exercises 1 - 2, determine the area of the region between the two curves in the given figure by integrating over the \(x\)-axis.
1) \(y=x^2−3\) and \(y=1\)
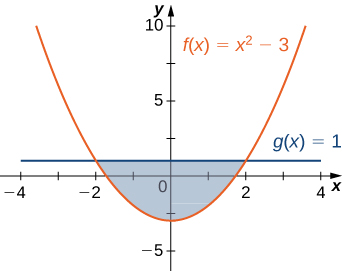
- Answer:
- \(\dfrac{32}{3} \, \text{units}^2\)
2) \(y=x^2\) and \(y=3x+4\)
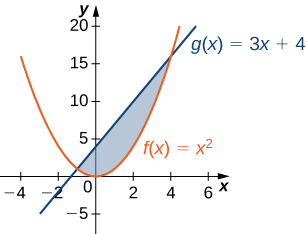
For exercises 3 - 4, split the region between the two curves into two smaller regions, then determine the area by integrating over the \(x\)-axis. Note that you will have two integrals to solve.
3) \(y=x^3\) and \( y=x^2+x\)
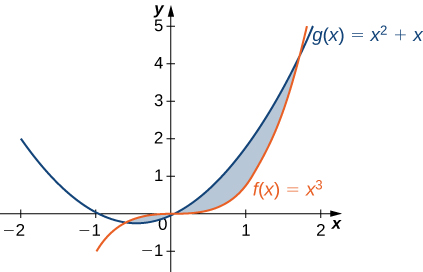
- Answer:
- \(\dfrac{13}{12}\, \text{units}^2\)
4) \(y=\cos θ\) and \( y=0.5\), for \( 0≤θ≤π\)
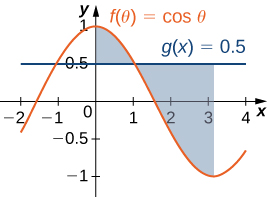
For exercises 5-6, determine the area of the region between the two curves by integrating over the \(y\)-axis.
5) \(x=y^2\) and \(x=9\)
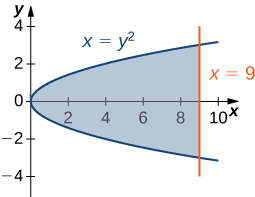
- Answer:
- \(36 \, \text{units}^2\)
6) \(y=x\) and \( x=y^2\)
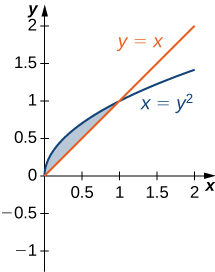
For exercises 7 - 13, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the \(x\)-axis.
7) \(y=x^2\) and \(y=−x^2+18x\)
- Answer:
-
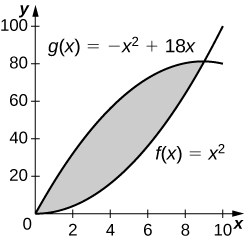
243 square units
8) \(y=\dfrac{1}{x}, \quad y=\dfrac{1}{x^2}\), and \(x=3\)
9) \(y=\cos x\) and \(y=\cos^2x\) on \(x \in [−π,π]\)
- Answer:
-
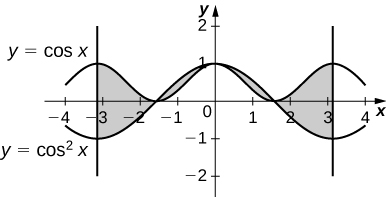
4 square units
10) \(y=e^x,\quad y=e^{2x−1}\), and \(x=0\)
11) \(y=e^x, \quad y=e^{−x}, \quad x=−1\) and \(x=1\)
- Answer:
-
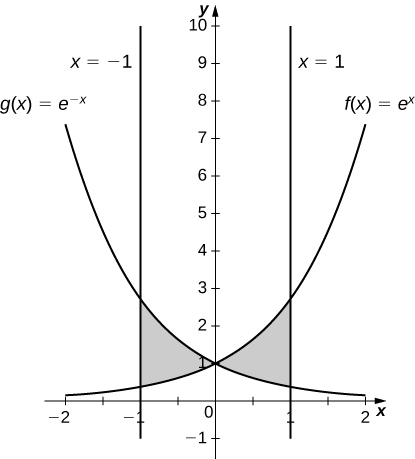
\(\dfrac{2(e−1)^2}{e}\, \text{units}^2\)
12) \( y=e, \quad y=e^x,\) and \(y=e^{−x}\)
13) \(y=|x|\) and \(y=x^2\)
- Answer:
-
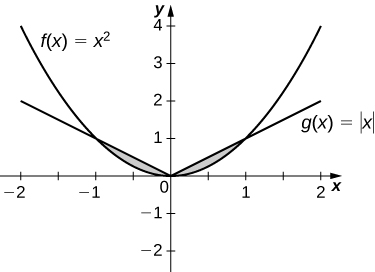
\(\dfrac{1}{3}\, \text{units}^2\)
For exercises 14 - 19, graph the equations and shade the area of the region between the curves. If necessary, break the region into sub-regions to determine its entire area.
14) \(y=\sin(πx),\quad y=2x,\) and \(x>0\)
15) \(y=12−x,\quad y=\sqrt{x},\) and \(y=1\)
- Answer:
-
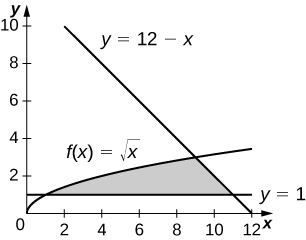
\(\dfrac{34}{3}\, \text{units}^2\)
16) \(y=\sin x\) and \(y=\cos x\) over \(x \in [−π,π]\)
17) \(y=x^3\) and \(y=x^2−2x\) over \(x \in [−1,1]\)
- Answer:
-
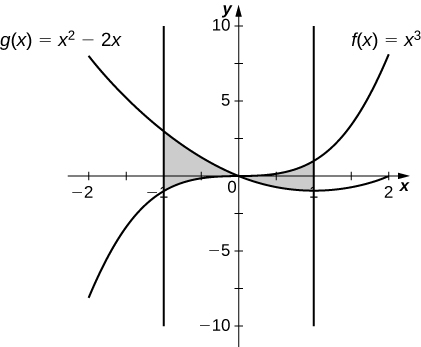
\(\dfrac{5}{2}\, \text{units}^2\)
18) \(y=x^2+9\) and \( y=10+2x\) over \(x \in [−1,3]\)
19) \(y=x^3+3x\) and \(y=4x\)
- Answer:
-
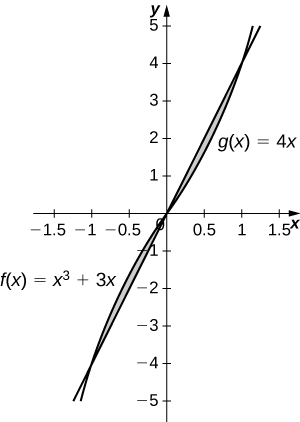
\(\dfrac{1}{2}\, \text{units}^2\)
For exercises 20 -25, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the \(y\)-axis.
20) \(x=y^3\) and \( x = 3y−2\)
21) \(x=y\) and \( x=y^3−y\)
- Answer:
-
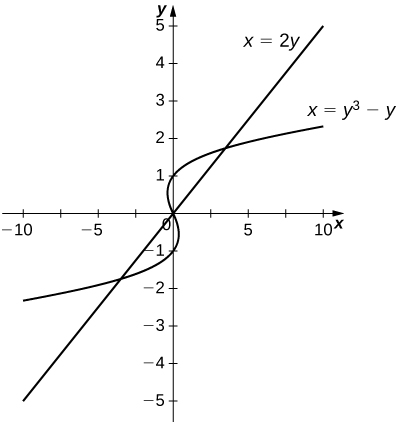
\(\dfrac{9}{2}\, \text{units}^2\)
22) \(x=−3+y^2\) and \( x=y−y^2\)
23) \(y^2=x\) and \(x=y+2\)
- Answer:
-
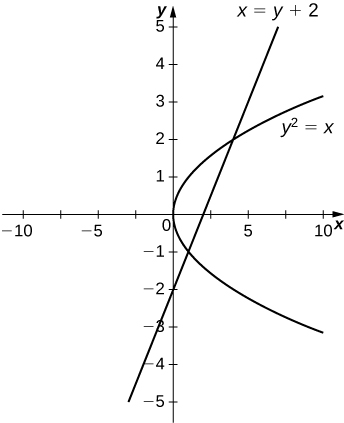
\(\dfrac{9}{2}\, \text{units}^2\)
24) \(x=|y|\) and \(2x=−y^2+2\)
25) \(x=\sin y,\quad x=\cos(2y),\quad y=π/2\), and \( y=−π/2\)
- Answer:
-
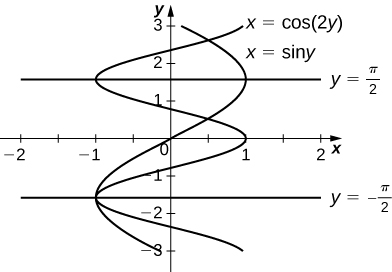
\(\dfrac{3\sqrt{3}}{2}\, \text{units}^2\)
For exercises 26 - 37, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the \(x\)-axis or \(y\)-axis, whichever seems more convenient.
26) \(x=y^4\) and \(x=y^5\)
27) \(y=xe^x,\quad y=e^x,\quad x=0\), and \(x=1\).
- Answer:
-
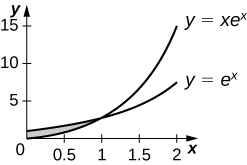
\(e^{−2}\, \text{units}^2\)
28) \(y=x^6\) and \(y=x^4\)
29) \(x=y^3+2y^2+1\) and \(x=−y^2+1\)
- Answer:
-
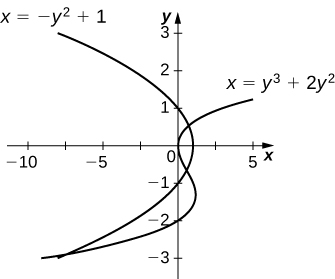
\(\dfrac{27}{4}\, \text{units}^2\)
30) \( y=|x|\) and \( y=x^2−1\)
31) \(y=4−3x\) and \(y=\dfrac{1}{x}\)
- Answer:
-
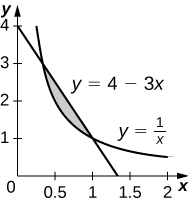
\(\left(\dfrac{4}{3}−\ln(3)\right)\, \text{units}^2\)
32) \(y=\sin x,\quad x=−π/6,\quad x=π/6,\) and \(y=\cos^3 x\)
33) \(y=x^2−3x+2\) and \( y=x^3−2x^2−x+2\)
- Answer:
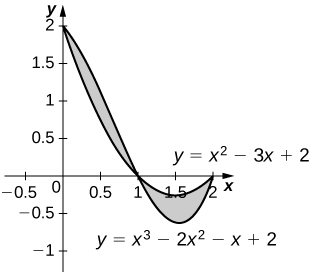
\(\dfrac{1}{2}\) square units
34) \(y=2\cos^3(3x),\quad y=−1,\quad x=\dfrac{π}{4},\) and \( x=−\dfrac{π}{4}\)
35) \(y+y^3=x\) and \(2y=x\)
- Answer:
-
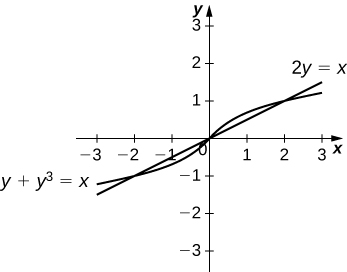
\(\dfrac{1}{2}\) square units
36) \( y=\sqrt{1−x^2}\) and \(y=x^2−1\)
37) \(y=\cos^{−1}x,\quad y=\sin^{−1}x,\quad x=−1,\) and \( x=1\)
- Answer:
-
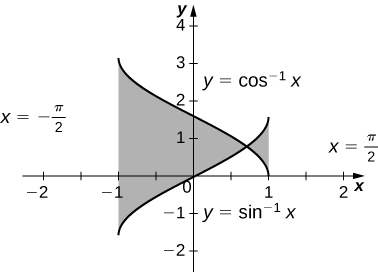
\(−2(\sqrt{2}−π)\) square units
For exercises 38 - 47, find the exact area of the region bounded by the given equations if possible. If you are unable to determine the intersection points analytically, use a calculator to approximate the intersection points with three decimal places and determine the approximate area of the region.
38) [T] \(x=e^y\) and \(y=x−2\)
39) [T] \(y=x^2\) and \(y=\sqrt{1−x^2}\)
- Answer:
- \(1.067\) square units
40) [T] \(y=3x^2+8x+9\) and \(3y=x+24\)
41) [T] \(x=\sqrt{4−y^2}\) and \( y^2=1+x^2\)
- Answer:
- \(0.852\) square units
42) [T] \(x^2=y^3\) and \(x=3y\)
43) [T] \(y=\sin^3x+2,\quad y=\tan x,\quad x=−1.5,\) and \(x=1.5\)
- Answer:
- \(7.523\) square units
44) [T] \(y=\sqrt{1−x^2}\) and \(y^2=x^2\)
45) [T] \(y=\sqrt{1−x^2}\) and \(y=x^2+2x+1\)
- Answer:
- \(\dfrac{3π−4}{12}\) square units
46) [T] \(x=4−y^2\) and \( x=1+3y+y^2\)
47) [T] \(y=\cos x,\quad y=e^x,\quad x=−π,\quad\) and\(\quad x=0\)
- Answer:
- \(1.429\) square units
48) The largest triangle with a base on the \(x\)-axis that fits inside the upper half of the unit circle \(y^2+x^2=1\) is given by \( y=1+x\) and \( y=1−x\). See the following figure. What is the area inside the semicircle but outside the triangle?
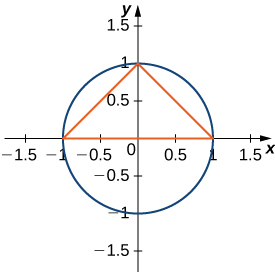
49) A factory selling cell phones has a marginal cost function \(C(x)=0.01x^2−3x+229\), where \(x\) represents the number of cell phones, and a marginal revenue function given by \(R(x)=429−2x.\) Find the area between the graphs of these curves and \(x=0.\) What does this area represent?
- Answer:
- $33,333.33 total profit for 200 cell phones sold
50) An amusement park has a marginal cost function \(C(x)=1000e−x+5\), where \(x\) represents the number of tickets sold, and a marginal revenue function given by \(R(x)=60−0.1x\). Find the total profit generated when selling \(550\) tickets. Use a calculator to determine intersection points, if necessary, to two decimal places.
51) The tortoise versus the hare: The speed of the hare is given by the sinusoidal function \(H(t)=1−\cos((πt)/2)\) whereas the speed of the tortoise is \(T(t)=(1/2)\tan^{−1}(t/4)\), where \(t\) is time measured in hours and the speed is measured in miles per hour. Find the area between the curves from time \(t=0\) to the first time after one hour when the tortoise and hare are traveling at the same speed. What does it represent? Use a calculator to determine the intersection points, if necessary, accurate to three decimal places.
- Answer:
- \(3.263\) mi represents how far ahead the hare is from the tortoise
52) The tortoise versus the hare: The speed of the hare is given by the sinusoidal function \(H(t)=(1/2)−(1/2)\cos(2πt)\) whereas the speed of the tortoise is \(T(t)=\sqrt{t}\), where \(t\) is time measured in hours and speed is measured in kilometers per hour. If the race is over in 1 hour, who won the race and by how much? Use a calculator to determine the intersection points, if necessary, accurate to three decimal places.
For exercises 53 - 55, find the area between the curves by integrating with respect to \(x\) and then with respect to \(y\). Is one method easier than the other? Do you obtain the same answer?
53) \(y=x^2+2x+1\) and \(y=−x^2−3x+4\)
- Answer:
- \(\dfrac{343}{24}\) square units
54) \(y=x^4\) and \(x=y^5\)
55) \(x=y^2−2\) and \(x=2y\)
- Answer:
- \(4\sqrt{3}\) square units
For exercises 56 - 57, solve using calculus, then check your answer with geometry.
56) Determine the equations for the sides of the square that touches the unit circle on all four sides, as seen in the following figure. Find the area between the perimeter of this square and the unit circle. Is there another way to solve this without using calculus?
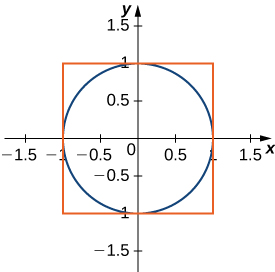
57) Find the area between the perimeter of the unit circle and the triangle created from \(y=2x+1,\,y=1−2x\) and \(y=−\dfrac{3}{5}\), as seen in the following figure. Is there a way to solve this without using calculus?
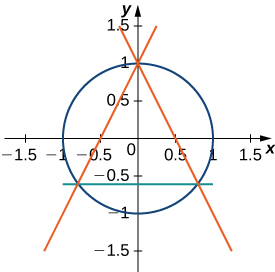
- Answer:
- \( \left(π−\dfrac{32}{25}\right)\) square units
6.2: Determining Volumes by Slicing
1) Derive the formula for the volume of a sphere using the slicing method.
2) Use the slicing method to derive the formula for the volume of a cone.
3) Use the slicing method to derive the formula for the volume of a tetrahedron with side length \(a.\)
4) Use the disk method to derive the formula for the volume of a trapezoidal cylinder.
5) Explain when you would use the disk method versus the washer method. When are they interchangeable?
Volumes by Slicing
For exercises 6 - 10, draw a typical slice and find the volume using the slicing method for the given volume.
6) A pyramid with height 6 units and square base of side 2 units, as pictured here.
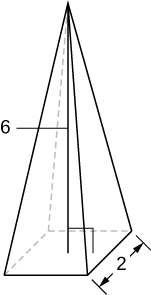
- Solution:
- Here the cross-sections are squares taken perpendicular to the \(y\)-axis.
We use the vertical cross-section of the pyramid through its center to obtain an equation relating \(x\) and \(y\).
Here this would be the equation, \( y = 6 - 6x \). Since we need the dimensions of the square at each \(y\)-level, we solve this equation for \(x\) to get, \(x = 1 - \tfrac{y}{6}\).
This is half the distance across the square cross-section at the \(y\)-level, so the side length of the square cross-section is, \(s = 2\left(1 - \tfrac{y}{6}\right).\)
Thus, we have the area of a cross-section is,
\(A(y) = \left[2\left(1 - \tfrac{y}{6}\right)\right]^2 = 4\left(1 - \tfrac{y}{6}\right)^2.\)
\(\begin{align*} \text{Then},\quad V &= \int_0^6 4\left(1 - \tfrac{y}{6}\right)^2 \, dy \\[5pt]
&= -24 \int_1^0 u^2 \, du, \quad \text{where} \, u = 1 - \tfrac{y}{6}, \, \text{so} \, du = -\tfrac{1}{6}\,dy, \quad \implies \quad -6\,du = dy \\[5pt]
&= 24 \int_0^1 u^2 \, du = 24\dfrac{u^3}{3}\bigg|_0^1 \\[5pt]
&= 8u^3\bigg|_0^1 \\[5pt]
&= 8\left( 1^3 - 0^3 \right) \quad= \quad 8\, \text{units}^3 \end{align*}\)
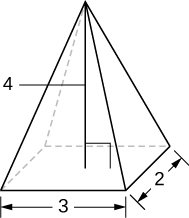
7) A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.
8) A tetrahedron with a base side of 4 units,as seen here.
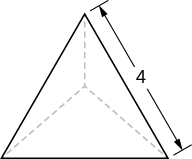
- Answer:
- \(V = \frac{32}{3\sqrt{2}} = \frac{16\sqrt{2}}{3}\) units3
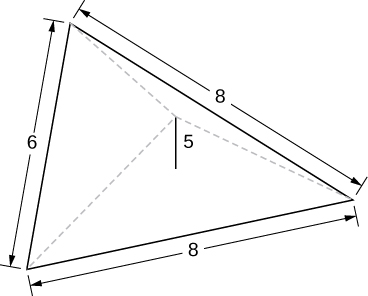
9) A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.
10) A cone of radius \( r\) and height \( h\) has a smaller cone of radius \( r/2\) and height \( h/2\) removed from the top, as seen here. The resulting solid is called a frustum.
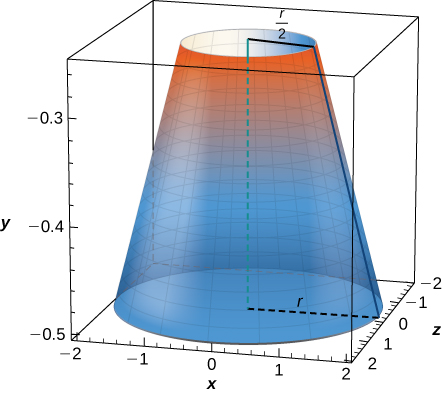
- Answer:
- \(V = \frac{7\pi}{12} hr^2\) units3
For exercises 11 - 16, draw an outline of the solid and find the volume using the slicing method.
11) The base is a circle of radius \( a\). The slices perpendicular to the base are squares.
12) The base is a triangle with vertices \( (0,0),(1,0),\) and \( (0,1)\). Slices perpendicular to the \(xy\)-plane are semicircles.
- Answer:
-
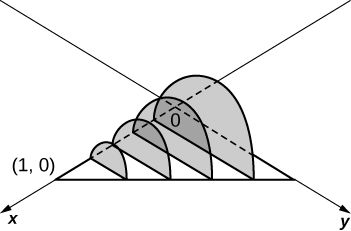
\(\displaystyle V = \int_0^1 \frac{\pi(1-x)^2}{8}\, dx \quad = \quad \frac{π}{24}\) units3
13) The base is the region under the parabola \( y=1−x^2\) in the first quadrant. Slices perpendicular to the \(xy\)-plane are squares.
14) The base is the region under the parabola \( y=1−x^2\) and above the \(x\)-axis. Slices perpendicular to the \(y\)-axis are squares.
- Answer:
-
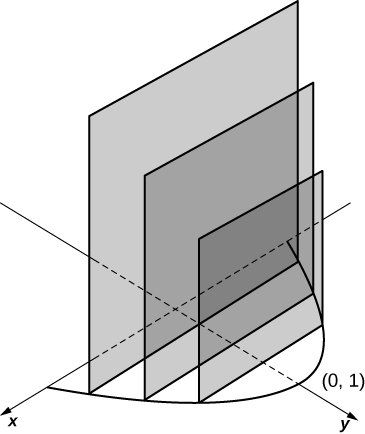
\(\displaystyle V = \int_0^1 4(1 - y)\,dy \quad = \quad 2\) units3
15) The base is the region enclosed by \( y=x^2)\) and \( y=9.\) Slices perpendicular to the \(x\)-axis are right isosceles triangles.
16) The base is the area between \( y=x\) and \( y=x^2\). Slices perpendicular to the \(x\)-axis are semicircles.
- Answer:
-
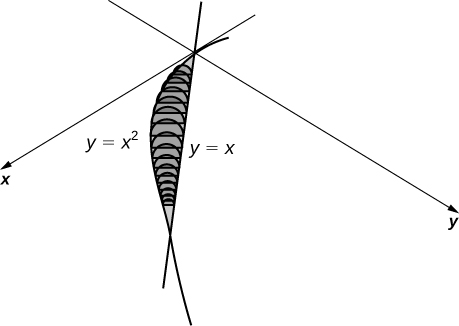
\(\displaystyle V = \int_0^1 \frac{\pi}{8}\left( x - x^2 \right)^2 \, dx \quad=\quad \frac{π}{240}\) units3
Disk and Washer Method
For exercises 17 - 24, draw the region bounded by the curves. Then, use the disk or washer method to find the volume when the region is rotated around the \(x\)-axis.
17) \( x+y=8,\quad x=0\), and \( y=0\)
18) \( y=2x^2,\quad x=0,\quad x=4,\) and \( y=0\)
- Answer:
-
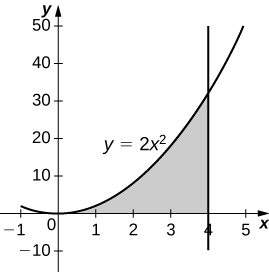
\(\displaystyle V = \int_0^4 4\pi x^4\, dx \quad=\quad \frac{4096π}{5}\) units3
19) \( y=e^x+1,\quad x=0,\quad x=1,\) and \( y=0\)
20) \( y=x^4,\quad x=0\), and \( y=1\)
- Answer:
-
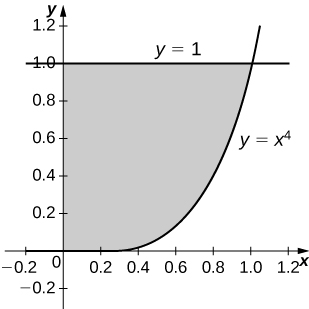
\(\displaystyle V = \int_0^1 \pi\left( 1^2 - \left( x^4\right)^2\right)\, dx = \int_0^1 \pi\left( 1 - x^8\right)\, dx \quad = \quad \frac{8π}{9}\) units3
21) \( y=\sqrt{x},\quad x=0,\quad x=4,\) and \( y=0\)
22) \( y=\sin x,\quad y=\cos x,\) and \( x=0\)
- Answer:
-
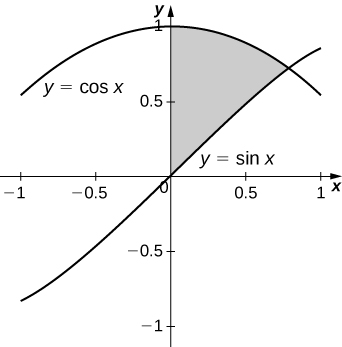
\(\displaystyle V = \int_0^{\pi/4} \pi \left( \cos^2 x - \sin^2 x\right) \, dx = \int_0^{\pi/4} \pi \cos 2x \, dx \quad=\quad \frac{π}{2}\) units3
23) \( y=\dfrac{1}{x},\quad x=2\), and \( y=3\)
24) \( x^2−y^2=9\) and \( x+y=9,\quad y=0\) and \( x=0\)
- Answer:
-
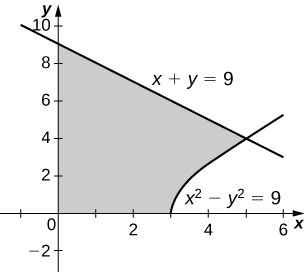
\(V = 207π\) units3
For exercises 25 - 32, draw the region bounded by the curves. Then, find the volume when the region is rotated around the \(y\)-axis.
25) \( y=4−\dfrac{1}{2}x,\quad x=0,\) and \( y=0\)
26) \( y=2x^3,\quad x=0,\quad x=1,\) and \( y=0\)
- Answer:
-
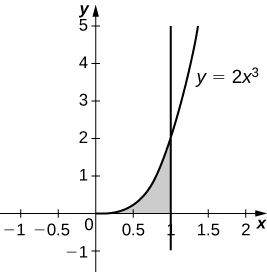
\(V = \frac{4π}{5}\) units3
27) \( y=3x^2,\quad x=0,\) and \( y=3\)
28) \( y=\sqrt{4−x^2},\quad y=0,\) and \( x=0\)
- Answer:
-
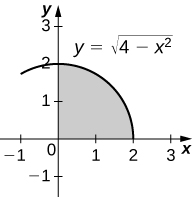
\(V = \frac{16π}{3}\) units3
29) \( y=\dfrac{1}{\sqrt{x+1}},\quad x=0\), and \( x=3\)
30) \( x=\sec(y)\) and \( y=\dfrac{π}{4},\quad y=0\) and \( x=0\)
- Answer:
-
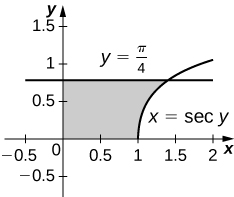
\(V = π\) units3
31) \( y=\dfrac{1}{x+1},\quad x=0\), and \( x=2\)
32) \( y=4−x,\quad y=x,\) and \( x=0\)
- Answer:
-
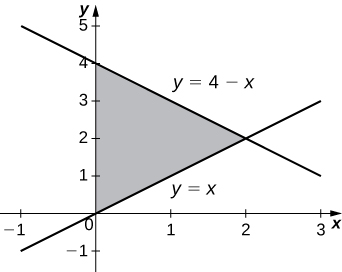
\(V = \frac{16π}{3}\) units3
For exercises 33 - 40, draw the region bounded by the curves. Then, find the volume when the region is rotated around the \(x\)-axis.
33) \( y=x+2,\quad y=x+6,\quad x=0\), and \( x=5\)
34) \( y=x^2\) and \( y=x+2\)
- Answer:
-
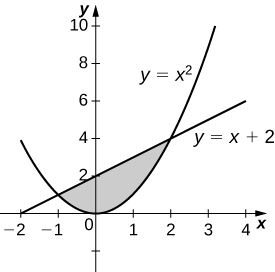
\(V = \frac{72π}{5}\) units3
35) \( x^2=y^3\) and \( x^3=y^2\)
36) \( y=4−x^2\) and \( y=2−x\)
- Answer:
-
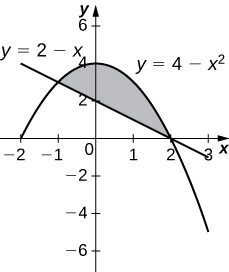
\(V = \frac{108π}{5}\) units3
37) [T] \( y=\cos x,\quad y=e^{−x},\quad x=0\), and \( x=1.2927\)
38) \( y=\sqrt{x}\) and \( y=x^2\)
- Answer:
-
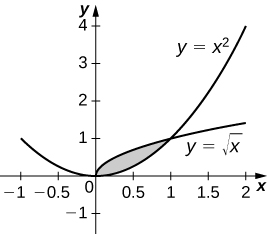
\(V = \frac{3π}{10}\) units3
39) \( y=\sin x,\quad y=5\sin x,\quad x=0\) and \( x=π\)
40) \( y=\sqrt{1+x^2}\) and \( y=\sqrt{4−x^2}\)
- Answer:
-
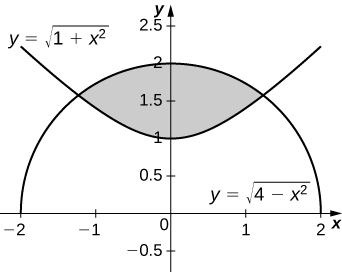
\(V = 2\sqrt{6}π\) units3
For exercises 41 - 45, draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the \(y\)-axis.
41) \( y=\sqrt{x},\quad x=4\), and \( y=0\)
42) \( y=x+2,\quad y=2x−1\), and \( x=0\)
- Answer:
-
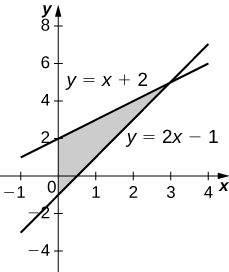
\(V = 9π\) units3
43) \( y=\dfrac{3}{x}\) and \( y=x^3\)
44) \( x=e^{2y},\quad x=y^2,\quad y=0\), and \( y=\ln(2)\)
- Answer:
-
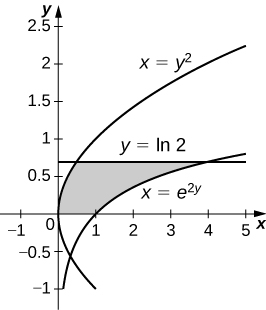
\(V = \dfrac{π}{20}(75−4\ln^5(2))\) units3
45) \( x=\sqrt{9−y^2},\quad x=e^{−y},\quad y=0\), and \( y=3\)
46) Yogurt containers can be shaped like frustums. Rotate the line \( y=\left(\frac{1}{m}\right)x\) around the \(y\)-axis to find the volume between \( y=a\) and \( y=b\).
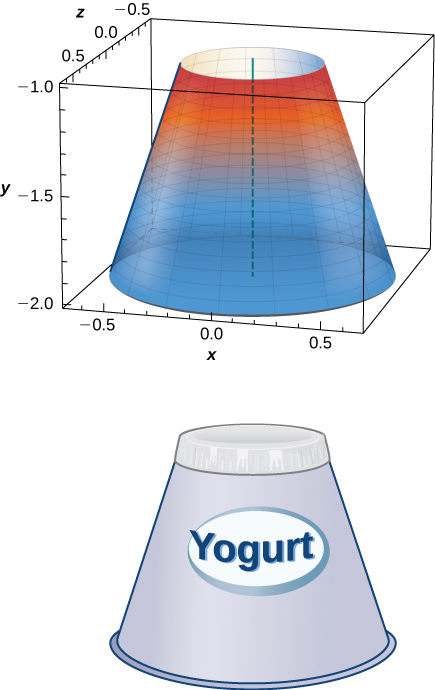
- Answer:
- \(V = \dfrac{m^2π}{3}(b^3−a^3)\) units3
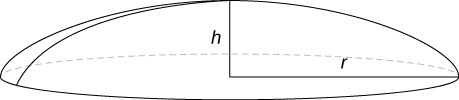
47) Rotate the ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) around the \(x\)-axis to approximate the volume of a football, as seen here.
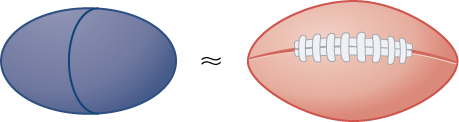
48) Rotate the ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) around the \(y\)-axis to approximate the volume of a football.
- Answer:
- \(V = \frac{4a^2bπ}{3}\) units3
49) A better approximation of the volume of a football is given by the solid that comes from rotating \( y=\sin x) around the \(x\)-axis from \( x=0\) to \( x=π\). What is the volume of this football approximation, as seen here?
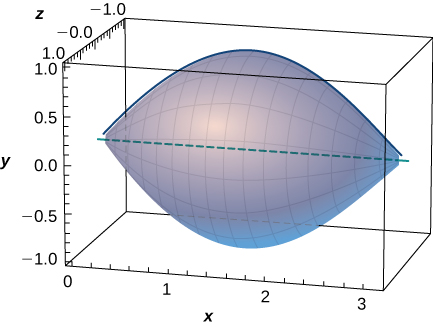
For exercises 51 - 56, find the volume of the solid described.
51) The base is the region between \( y=x\) and \( y=x^2\). Slices perpendicular to the \(x\)-axis are semicircles.
52) The base is the region enclosed by the generic ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.\) Slices perpendicular to the \(x\)-axis are semicircles.
- Answer:
- \(V = \frac{2ab^2π}{3}\) units3
53) Bore a hole of radius a down the axis of \(a\) right cone and through the base of radius \(b\), as seen here.
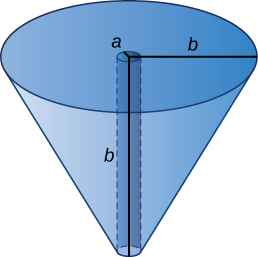
54) Find the volume common to two spheres of radius \(r\) with centers that are \(2h\) apart, as shown here.
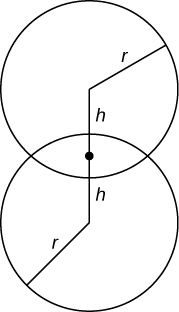
- Answer:
- \(V = \frac{π}{12}(r+h)^2(6r−h)\) units3
55) Find the volume of a spherical cap of height \(h\) and radius \(r\) where \(h<r\), as seen here.
56) Find the volume of a sphere of radius \(R\) with a cap of height \(h\) removed from the top, as seen here.
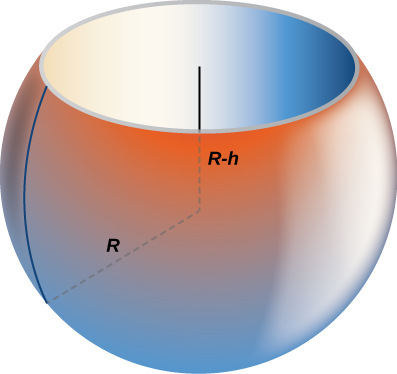
- Answer:
- \(V = \dfrac{π}{3}(h+R)(h−2R)^2\) units3
6.3: Volumes of Revolution: Cylindrical Shells
For exercises 1 - 6, find the volume generated when the region between the two curves is rotated around the given axis. Use both the shell method and the washer method. Use technology to graph the functions and draw a typical slice by hand.
1) [T] Over the curve of \( y=3x,\) \(x=0,\) and \( y=3\) rotated around the \(y\)-axis.
2) [T] Under the curve of \( y=3x,\) \(x=0\), and \( x=3\) rotated around the \(y\)-axis.
- Answer:
-
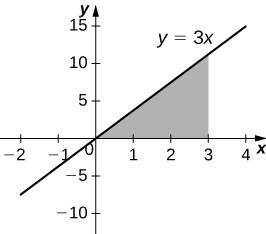
\(V = 54π\) units3
3) [T] Over the curve of \( y=3x,\) \(x=0\), and \( y=3\) rotated around the \(x\)-axis.
4) [T] Under the curve of \( y=3x,\) \(x=0,\) and \( x=3\) rotated around the \(x\)-axis.
- Answer:
-
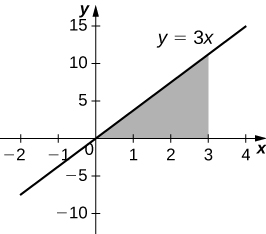
\(V = 81π\) units3
5) [T] Under the curve of \( y=2x^3,\;x=0,\) and \( x=2\) rotated around the \(y\)-axis.
6) [T] Under the curve of \( y=2x^3,\;x=0,\) and \( x=2\) rotated around the \(x\)-axis.
- Answer:
-
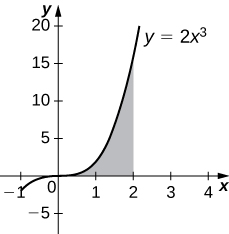
\(V = \frac{512π}{7}\) units3
For exercises 7 - 16, use shells to find the volumes of the given solids. Note that the rotated regions lie between the curve and the \(x\)-axis and are rotated around the \(y\)-axis.
7) \( y=1−x^2,\) \(x=0,\) and \( x=1\)
8) \( y=5x^3,\) \(x=0\), and \( x=1\)
- Answer:
- \(V = 2π\) units3
9) \( y=\dfrac{1}{x},\) \(x=1,\) and \( x=100\)
10) \( y=\sqrt{1−x^2},\) \(x=0\), and \( x=1\)
- Answer:
- \(V= \frac{2π}{3}\) units3
11) \( y=\dfrac{1}{1+x^2},\) \(x=0\),and \( x=3\)
12) \( y=\sin x^2,x=0\), and \( x=\sqrt{π}\)
- Answer:
- \(V= 2π\) units3
13) \( y=\dfrac{1}{\sqrt{1−x^2}},\) \(x=0\), and \( x=\frac{1}{2}\)
14) \( y=\sqrt{x},\) \(x=0\), and \( x=1\)
- Answer:
- \(V = \frac{4π}{5}\) units3
15) \( y=(1+x^2)^3,\) \(x=0\), and \( x=1\)
16) \( y=5x^3−2x^4,\) \(x=0\), and \( x=2\)
- Answer:
- \(V= \frac{64π}{3}\) units3
For exercises 17 - 26, use shells to find the volume generated by rotating the regions between the given curve and \( y=0\) around the \(x\)-axis.
17) \( y=\sqrt{1−x^2},\) \(x=0\), and \( x=1\)
18) \( y=x^2,\) \(x=0\), and \( x=2\)
- Answer:
- \(V = \frac{32π}{5}\) units3
19) \( y=e^x,\) \(x=0\), and \( x=1\)
20) \( y=\ln(x),\) \(x=1\), and \( x=e\)
- Answer:
- \(V= π(e−2)\) units3
21) \( x=\dfrac{1}{1+y^2},\) \(y=1\), and \( y=4\)
22) \( x=\dfrac{1+y^2}{y},\) \(y=0\), and \( y=2\)
- Answer:
- \(V= \frac{28π}{3}\) units3
23) \( x=\cos y,\) \(y=0\), and \( y=π\)
24) \( x=y^3−4y^2,\) \(x=−1\), and \( x=2\)
- Answer:
- \(V= \frac{84π}{5}\) units3
25) \( x=ye^y,\) \(x=−1\), and \( x=2\)
26) \( x=e^y\cos y,\) \(x=0\), and \( x=π\)
- Answer:
- \(V = e^ππ^2\) units3
For exercises 27 - 36, find the volume generated when the region between the curves is rotated around the given axis.
27) \( y=3−x\), \(y=0\), \(x=0\), and \( x=2\) rotated around the \(y\)-axis.
28) \( y=x^3\), \(y=0\), \(x=0\), and \( y=8\) rotated around the \(y\)-axis.
- Answer:
- \( V=\frac{64π}{5}\) units3
29) \( y=x^2,\) \(y=x,\) rotated around the \(y\)-axis.
30) \( y=\sqrt{x},\) \(x=0\), and \( x=1\) rotated around the line \( x=2.\)
- Answer:
- \(V=\frac{28π}{15}\) units3
31) \( y=\dfrac{1}{4−x},\) \(x=1,\) and \( x=2\) rotated around the line \( x=4\).
32) \( y=\sqrt{x}\) and \( y=x^2\) rotated around the \(y\)-axis.
- Answer:
- \(V=\frac{3π}{10}\) units3
33) \( y=\sqrt{x}\) and \( y=x^2\) rotated around the line \( x=2\).
34) \( x=y^3,\) \(y=\dfrac{1}{x},\) \(x=1\), and \( y=2\) rotated around the \(x\)-axis.
- Answer:
- \( \frac{52π}{5}\) units3
35) \( x=y^2\) and \( y=x\) rotated around the line \( y=2\).
36) [T] Left of \( x=\sin(πy)\), right of \( y=x\), around the \(y\)-axis.
- Answer:
- \(V \approx 0.9876\) units3
For exercises 37 - 44, use technology to graph the region. Determine which method you think would be easiest to use to calculate the volume generated when the function is rotated around the specified axis. Then, use your chosen method to find the volume.
37) [T] \( y=x^2\) and \( y=4x\) rotated around the \(y\)-axis.
38) [T] \( y=\cos(πx),y=\sin(πx),x=\frac{1}{4}\), and \( x=\frac{5}{4}\) rotated around the \(y\)-axis.
- Answer:
-
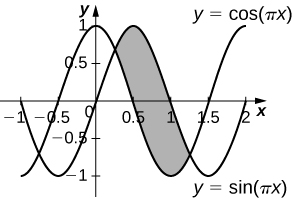
\(V = 3\sqrt{2}\) units3
39) [T] \( y=x^2−2x,\; x=2,\) and \( x=4\) rotated around the \(y\)-axis.
40) [T] \( y=x^2−2x,\; x=2,\) and \( x=4\) rotated around the \(x\)-axis.
- Answer:
-
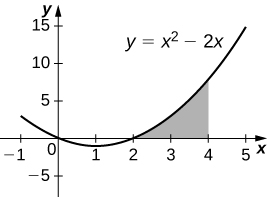
\(V= \frac{496π}{15}\) units3
41) [T] \( y=3x^3−2,\; y=x\), and \( x=2\) rotated around the \(x\)-axis.
42) [T] \( y=3x^3−2,\; y=x\), and \( x=2\) rotated around the \(y\)-axis.
- Answer:
-
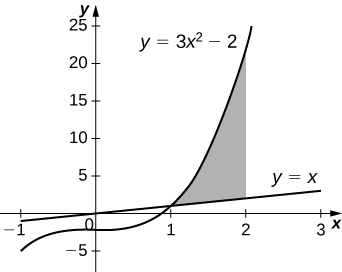
\( V = \frac{398π}{15}\) units3
43) [T] \( x=\sin(πy^2)\) and \( x=\sqrt{2}y\) rotated around the \(x\)-axis.
44) [T] \( x=y^2,\; x=y^2−2y+1\), and \( x=2\) rotated around the \(y\)-axis.
- Answer:
-
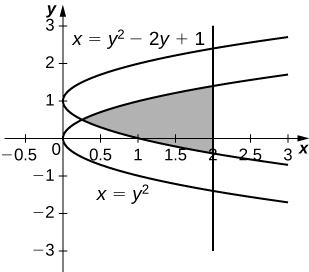
\( V =15.9074\) units3
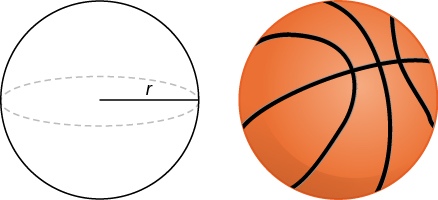
For exercises 45 - 51, use the method of shells to approximate the volumes of some common objects, which are pictured in accompanying figures.
45) Use the method of shells to find the volume of a sphere of radius \( r\).
46) Use the method of shells to find the volume of a cone with radius \( r\) and height \( h\).
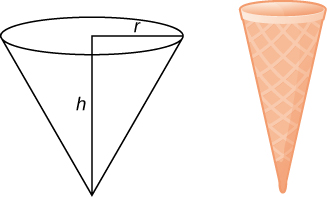
- Answer:
- \(V = \frac{1}{3}πr^2h\) units3
47) Use the method of shells to find the volume of an ellipse \( (x^2/a^2)+(y^2/b^2)=1\) rotated around the \(x\)-axis.
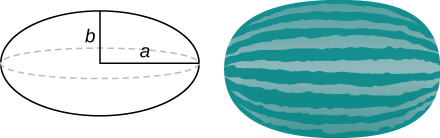
48) Use the method of shells to find the volume of a cylinder with radius \( r\) and height \( h\).
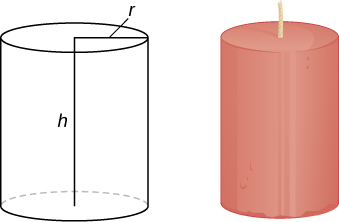
- Answer:
- \(V= πr^2h\) units3
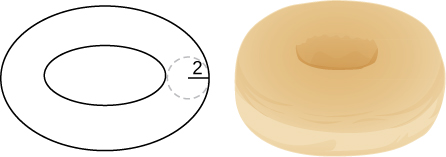
49) Use the method of shells to find the volume of the donut created when the circle \( x^2+y^2=4\) is rotated around the line \( x=4\).
50) Consider the region enclosed by the graphs of \( y=f(x),\; y=1+f(x),\; x=0,\; y=0,\) and \( x=a>0\). What is the volume of the solid generated when this region is rotated around the \(y\)-axis? Assume that the function is defined over the interval \( [0,a]\).
- Answer:
- \( V=πa^2\) units3
51) Consider the function \( y=f(x)\), which decreases from \( f(0)=b\) to \( f(1)=0\). Set up the integrals for determining the volume, using both the shell method and the disk method, of the solid generated when this region, with \( x=0\) and \( y=0\), is rotated around the \(y\)-axis. Prove that both methods approximate the same volume. Which method is easier to apply? (Hint: Since \( f(x)\) is one-to-one, there exists an inverse \( f^{−1}(y)\).)
6.4: Arc Length of a Curve and Surface Area
For exercises 1 - 3, find the length of the functions over the given interval.
1) \( y=5x\) from \( x=0\) to \( x=2\)
- Answer:
- \(s = 2\sqrt{26}\) units
2) \( y=−\frac{1}{2}x+25\) from \( x=1\) to \( x=4\)
3) \( x=4y\) from \( y=−1\) to \( y=1\)
- Answer:
- \( s = 2\sqrt{17}\) units
4) Pick an arbitrary linear function \( x=g(y)\) over any interval of your choice \( (y_1,y_2).\) Determine the length of the function and then prove the length is correct by using geometry.
5) Find the surface area of the volume generated when the curve \( y=\sqrt{x}\) revolves around the \(x\)-axis from \( (1,1)\) to \( (4,2)\), as seen here.
- Answer:
- \(A = \frac{π}{6}(17\sqrt{17}−5\sqrt{5})\) units2
6) Find the surface area of the volume generated when the curve \( y=x^2\) revolves around the \(y\)-axis from \( (1,1)\) to \( (3,9)\).
For exercises 7 - 16, find the lengths of the functions of \(x\) over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.
7) \( y=x^{3/2}\) from \( (0,0)\) to \( (1,1)\)
- Answer:
- \(s= \frac{13\sqrt{13}−8}{27}\) units
8) \( y=x^{2/3}\) from \( (1,1)\) to \( (8,4)\)
9) \( y=\frac{1}{3}(x^2+2)^{3/2}\) from \( x=0\) to \( x=1\)
- Answer:
- \(s= \frac{4}{3}\) units
10) \( y=\frac{1}{3}(x^2−2)^{3/2}\) from \( x=2\) to \( x=4\)
11) [T] \( y=e^x\) on \( x=0\) to \( x=1\)
- Answer:
- \(s \approx 2.0035\) units
12) \( y=\dfrac{x^3}{3}+\dfrac{1}{4x}\) from \( x=1\) to \( x=3\)
13) \( y=\dfrac{x^4}{4}+\dfrac{1}{8x^2}\) from \( x=1\) to \( x=2\)
- Answer:
- \(s= \frac{123}{32}\) units
14) \( y=\dfrac{2x^{3/2}}{3}−\dfrac{x^{1/2}}{2}\) from \( x=1\) to \( x=4\)
15) \( y=\frac{1}{27}(9x^2+6)^{3/2}\) from \( x=0\) to \( x=2\)
- Answer:
- \(s=10\) units
16) [T] \( y=\sin x\) on \( x=0\) to \( x=π\)
For exercises 17 - 26, find the lengths of the functions of \(y\) over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.
17) \( y=\dfrac{5−3x}{4}\) from \( y=0\) to \( y=4\)
- Answer:
- \(s= \frac{20}{3}\) units
18) \( x=\frac{1}{2}(e^y+e^{−y})\) from \( y=−1\) to \( y=1\)
19) \( x=5y^{3/2}\) from \( y=0\) to \( y=1\)
- Answer:
- \(s= \frac{1}{675}(229\sqrt{229}−8)\) units
20) [T] \( x=y^2\) from \( y=0\) to \( y=1\)
21) \( x=\sqrt{y}\) from \( y=0\) to \( y=1\)
- Answer:
- \(s= \frac{1}{8}(4\sqrt{5}+\ln(9+4\sqrt{5}))\) units
22) \( x=\frac{2}{3}(y^2+1)^{3/2}\) from \( y=1\) to \( y=3\)
23) [T] \( x=\tan y\) from \( y=0\) to \( y=\frac{3}{4}\)
- Answer:
- \(s \approx 1.201\) units
24) [T] \( x=\cos^2y\) from \( y=−\frac{π}{2}\) to \( y=\frac{π}{2}\)
25) [T] \( x=4^y\) from \( y=0\) to \( y=2\)
- Answer:
- \(s \approx 15.2341\) units
26) [T] \( x=\ln(y)\) on \( y=\dfrac{1}{e}\) to \( y=e\)
For exercises 27 - 34, find the surface area of the volume generated when the following curves revolve around the \(x\)-axis. If you cannot evaluate the integral exactly, use your calculator to approximate it.
27) \( y=\sqrt{x}\) from \( x=2\) to \( x=6\)
- Answer:
- \(A= \frac{49π}{3}\) units2
28) \( y=x^3\) from \( x=0\) to \( x=1\)
29) \( y=7x\) from \( x=−1\) to \( x=1\)
- Answer:
- \(A = 70π\sqrt{2}\) units2
30) [T] \( y=\frac{1}{x^2}\) from \( x=1\) to \( x=3\)
31) \( y=\sqrt{4−x^2}\) from \( x=0\) to \( x=2\)
- Answer:
- \(A = 8π\) units2
32) \( y=\sqrt{4−x^2}\) from \( x=−1\) to \( x=1\)
33) \( y=5x\) from \( x=1\) to \( x=5\)
- Answer:
- \(A = 120π\sqrt{26}\) units2
34) [T] \( y=\tan x\) from \( x=−\frac{π}{4}\) to \( x=\frac{π}{4}\)
For exercises 35 - 42, find the surface area of the volume generated when the following curves revolve around the \(y\)-axis. If you cannot evaluate the integral exactly, use your calculator to approximate it.
35) \( y=x^2\) from \( x=0\) to \( x=2\)
- Answer:
- \(A= \frac{π}{6}(17\sqrt{17}−1)\) units2
36) \( y=\frac{1}{2}x^2+\frac{1}{2}\) from \( x=0\) to \( x=1\)
37) \( y=x+1\) from \( x=0\) to \( x=3\)
- Answer:
- \(A = 9\sqrt{2}π\) units2
38) [T] \( y=\dfrac{1}{x}\) from \( x=\dfrac{1}{2}\) to \( x=1\)
39) \( y=\sqrt[3]{x}\) from \( x=1\) to \( x=27\)
- Answer:
- \(A = \frac{10\sqrt{10}π}{27}(73\sqrt{73}−1)\) units2
40) [T] \( y=3x^4\) from \( x=0\) to \( x=1\)
41) [T] \( y=\dfrac{1}{\sqrt{x}}\) from \( x=1\) to \( x=3\)
- Answer:
- \(A \approx 25.645\) units2
42) [T] \( y=\cos x\) from \( x=0\) to \( x=\frac{π}{2}\)
43) The base of a lamp is constructed by revolving a quarter circle \( y=\sqrt{2x−x^2}\) around the \(y\)-axis from \( x=1\) to \( x=2\), as seen here. Create an integral for the surface area of this curve and compute it.
- Answer:
- \(A = 2π\) units2
44) A light bulb is a sphere with radius \(1/2\) in. with the bottom sliced off to fit exactly onto a cylinder of radius \(1/4\) in. and length \(1/3\) in., as seen here. The sphere is cut off at the bottom to fit exactly onto the cylinder, so the radius of the cut is \(1/4\) in. Find the surface area (not including the top or bottom of the cylinder).
45) [T] A lampshade is constructed by rotating \( y=1/x\) around the \(x\)-axis from \( y=1\) to \( y=2\), as seen here. Determine how much material you would need to construct this lampshade—that is, the surface area—accurate to four decimal places.
- Answer:
- \(10.5017\) units2
46) [T] An anchor drags behind a boat according to the function \( y=24e^{−x/2}−24\), where \( y\) represents the depth beneath the boat and \( x\) is the horizontal distance of the anchor from the back of the boat. If the anchor is \( 23\) ft below the boat, how much rope do you have to pull to reach the anchor? Round your answer to three decimal places.
47) [T] You are building a bridge that will span \( 10\) ft. You intend to add decorative rope in the shape of \( y=5|\sin((xπ)/5)|\), where \( x\) is the distance in feet from one end of the bridge. Find out how much rope you need to buy, rounded to the nearest foot.
- Answer:
- \( 23\) ft
For exercise 48, find the exact arc length for the following problems over the given interval.
48) \( y=\ln(\sin x)\) from \( x=π/4\) to \( x=(3π)/4\). (Hint: Recall trigonometric identities.)
49) Draw graphs of \(y=x^2, y=x^6\), and \(y=x^{10}\). For \( y=x^n\), as \( n\) increases, formulate a prediction on the arc length from \( (0,0)\) to \( (1,1)\). Now, compute the lengths of these three functions and determine whether your prediction is correct.
- Answer:
- \(2\)
50) Compare the lengths of the parabola \(x=y^2\) and the line \(x=by\) from \((0,0)\) to \((b^2,b)\) as \(b\) increases. What do you notice?
51) Solve for the length of \(x=y^2\) from \((0,0)\) to \((1,1)\). Show that \( x=\dfrac{y^2}{2}\) from \((0,0)\) to \((2,2)\) is twice as long. Graph both functions and explain why this is so.
- Answer:
- Answers may vary
52) [T] Which is longer between \((1,1)\) and \(\left(2,\frac{1}{2}\right)\): the hyperbola \(y=\dfrac{1}{x}\) or the graph of \(x+2y=3\)?
53) Explain why the surface area is infinite when \(y=1/x\) is rotated around the \(x\)-axis for \( 1≤x<∞,\) but the volume is finite.
- Answer:
- For more information, look up Gabriel’s Horn.
6.5: Physical Applications
Basic Work Problems
For exercises 1 - 6, find the work done.
1) Find the work done when a constant force \( F=12\) lb moves a chair from \( x=0.9\) to \( x=1.1\) ft.
2) How much work is done when a person lifts a \( 50\) lb box of comics onto a truck that is \( 3\) ft off the ground?
- Answer:
- \(W = 150\) ft-lb
3) What is the work done lifting a \( 20\) kg child from the floor to a height of \( 2\) m? (Note that \( 1\) kg equates to \( 9.8\) N)
4) Find the work done when you push a box along the floor \( 2\) m, when you apply a constant force of \( F=100\) N.
- Answer:
- \(W = 200\) J
5) Compute the work done for a force \( F=\dfrac{12}{x^2}\) N from \( x=1\) to \( x=2\) m.
6) What is the work done moving a particle from \( x=0\) to \( x=1\) m if the force acting on it is \( F=3x^2\) N?
- Answer:
- \(W = 1\) J
Density Problems
In exercises 7 - 11, find the mass of the one-dimensional object.
7) A wire that is \(2\) ft long (starting at \(x=0\)) and has a density function of \(ρ(x)=x^2+2x\) lb/ft
8) A car antenna that is \(3\) ft long (starting at \(x=0)\) and has a density function of \(ρ(x)=3x+2\) lb/ft
- Answer:
- \( \frac{39}{2}\)
9) A metal rod that is \( 8\) in. long (starting at \( x=0\)) and has a density function of \( ρ(x)=e^{1/2x}\) lb/in.
10) A pencil that is \( 4\) in. long (starting at \( x=2\)) and has a density function of \( ρ(x)=\dfrac{5}{x}\) oz/in.
- Answer:
- \( \ln(243)\)
11) A ruler that is \( 12\) in. long (starting at \( x=5\)) and has a density function of \( ρ(x)=\ln(x)+(1/2)x^2\) oz/in.
In exercises 12 - 16, find the mass of the two-dimensional object that is centered at the origin.
12) An oversized hockey puck of radius \( 2\) in. with density function \( ρ(x)=x^3−2x+5\)
- Answer:
- \( \frac{332π}{15}\)
13) A frisbee of radius \( 6\) in. with density function \( ρ(x)=e^{−x}\)
14) A plate of radius \( 10\) in. with density function \( ρ(x)=1+\cos(πx)\)
- Answer:
- \( 100π\)
15) A jar lid of radius \( 3\) in. with density function \(ρ(x)=\ln(x+1)\)
16) A disk of radius \(5\) cm with density function \(ρ(x)=\sqrt{3x}\)
- Answer:
- \(20π\sqrt{15}\)
Spring Work Problems
17) A \( 12\)-in. spring is stretched to \( 15\) in. by a force of \( 75\) lb. What is the spring constant?
18) A spring has a natural length of \( 10\) cm. It takes \( 2\) J to stretch the spring to \( 15\) cm. How much work would it take to stretch the spring from \( 15\) cm to \( 20\) cm?
- Answer:
- \(W = 6\) J
19) A \( 1\)-m spring requires \( 10\) J to stretch the spring to \( 1.1\) m. How much work would it take to stretch the spring from \( 1\) m to \( 1.2\) m?
20) A spring requires \( 5\) J to stretch the spring from \( 8\) cm to \( 12\) cm, and an additional \( 4\) J to stretch the spring from \( 12\) cm to \( 14\) cm. What is the natural length of the spring?
- Answer:
- The natural length is\( 5\) cm.
21) A shock absorber is compressed 1 in. by a weight of 1 ton. What is the spring constant?
22) A force of \( F=\left(20x−x^3\right)\) N stretches a nonlinear spring by \( x\) meters. What work is required to stretch the spring from \( x=0\) to \( x=2\) m?
- Answer:
- \(W = 36\) J
Cable and Chain Work Problems
23) Find the work done by winding up a hanging cable of length \( 100\) ft and weight-density \( 5\) lb/ft.
24) For the cable in the preceding exercise, how much work is done to lift the cable \( 50\) ft?
- Answer:
- \(W = 18,750\) ft-lb
25) For the cable in the preceding exercise, how much additional work is done by hanging a \( 200\) lb weight at the end of the cable?
Pyramid & Satellite/Rocket Work Problems
26) [T] A pyramid of height \( 500\) ft has a square base \( 800\) ft by \( 800\) ft. Find the area \( A\) at height \( h\). If the rock used to build the pyramid weighs approximately \( w=100\,\text{lb/ft}^3\), how much work did it take to lift all the rock?
- Answer:
- \(W= \frac{32}{3}×10^9\) ft-lb
27) [T] For the pyramid in the preceding exercise, assume there were \( 1000\) workers each working \( 10\) hours a day, \( 5\) days a week, \( 50\) weeks a year. If each of the workers, on average, lifted ten 100-lb rocks \( 2\) ft/hr, how long did it take to build the pyramid?
28) [T] The force of gravity on a mass \( m\) is \( F=−((GMm)/x^2)\) newtons. For a rocket of mass \( m=1000\) kg, compute the work to lift the rocket from \( x=6400\) to \( x=6500\) km. (Note: \( G=6×10^{−17}\,\text{N m}^2/\text{kg}^2\) and \( M=6×10^{24}\) kg.)
- Answer:
- \(W = 8.65×10^5\) J
29) [T] For the rocket in the preceding exercise, find the work to lift the rocket from \( x=6400\) to \( x=∞\).
Hydrostatic Force and Pressure
30) [T] A rectangular dam is \(40\) ft high and \(60\) ft wide. Compute the total force \(F\) on the dam when
a. the surface of the water is at the top of the dam and
b. the surface of the water is halfway down the dam.
- Answer:
- a. \(3,000,000\) lb,
b. \(749,000\) lb
Pumping Work Problems
31) [T] Find the work required to pump all the water out of a cylinder that has a circular base of radius \( 5\)ft and height \( 200\) ft. Use the fact that the density of water is \( 62\) lb/ft3.
32) [T] Find the work required to pump all the water out of the cylinder in the preceding exercise if the cylinder is only half full.
- Answer:
- \(W = 23.25π\) million ft-lb
33) [T] How much work is required to pump out a swimming pool if the area of the base is \(800 \, \text{ft}^2\), the water is \(4\) ft deep, and the top is \(1\) ft above the water level? Assume that the density of water is \( 62\) lb/ft3.
34) A cylinder of depth \(H\) and cross-sectional area \(A\) stands full of water at density \(ρ\). Compute the work to pump all the water to the top.
- Answer:
- \(W = \dfrac{AρH^2}{2}\)
35) For the cylinder in the preceding exercise, compute the work to pump all the water to the top if the cylinder is only half full.
36) A cone-shaped tank has a cross-sectional area that increases with its depth: \( A=\dfrac{πr^2h^2}{H^3}\). Show that the work to empty it is half the work for a cylinder with the same height and base.
- Answer:
- Answers may vary.
6.6: Moments and Centers of Mass
In exercises 1 - 6, calculate the center of mass for the collection of masses given.
1) \(m_1=2\) at \(x_1=1\) and \(m_2=4\) at \(x_2=2\)
2) \(m_1=1\) at \(x_1=−1\) and \(m_2=3\) at \(x_2=2\)
- Answer:
- \(x = \frac{5}{4}\)
3) \(m=3\) at \(x=0,1,2,6\)
4) Unit masses at \((x,y)=(1,0),(0,1),(1,1)\)
- Answer:
- \(\left(\frac{2}{3},\, \frac{2}{3}\right)\)
5) \(m_1=1\) at \((1,0)\) and \(m_2=4\) at \((0,1)\)
6) \(m_1=1\) at \((1,0)\) and \(m_2=3\) at \((2,2)\)
- Answer:
- \(\left(\frac{7}{4},\,\frac{3}{2}\right)\)
In exercises 7 - 16, compute the center of mass \(\bar x.\)
7) \(ρ=1\) for \(x∈(−1,3)\)
8) \(ρ=x^2\) for \(x∈(0,L)\)
- Answer:
- \(\dfrac{3L}{4}\)
9) \(ρ=1\) for \(x∈(0,1)\) and \(ρ=2\) for \(x∈(1,2)\)
10) \(ρ=\sin x\) for \(x∈(0,π)\)
- Answer:
- \(\frac{π}{2}\)
11) \(ρ=\cos x\) for \(x∈\left(0,\frac{π}{2}\right)\)
12) \(ρ=e^x\) for \(x∈(0,2)\)
- Answer:
- \(\dfrac{e^2+1}{e^2−1}\)
13) \(ρ=x^3+xe^{−x}\) for \(x∈(0,1)\)
14) \(ρ=x\sin x\) for \(x∈(0,π)\)
- Answer:
- \(\dfrac{π^2−4}{π}\)
15) \(ρ=\sqrt{x}\) for \(x∈(1,4)\)
16) \(ρ=\ln x\) for \(x∈(1,e)\)
- Answer:
- \(\frac{1}{4}(1+e^2)\)
In exercises 17 - 19, compute the center of mass \((\bar{x},\bar{y}).\) Use symmetry to help locate the center of mass whenever possible.
17) \(ρ=7\) in the square \(0≤x≤1, \; 0≤y≤1\)
18) \(ρ=3\) in the triangle with vertices \((0,0), \, (a,0)\), and \((0,b)\)
- Answer:
- \(\left(\frac{a}{3},\, \frac{b}{3}\right)\)
19) \(ρ=2\) for the region bounded by \(y=\cos(x), \; y=−\cos(x), \; x=−\frac{π}{2}\), and \(x=\frac{π}{2}\)
In exercises 20 - 26, use a calculator to draw the region, then compute the center of mass \((\bar{x},\bar{y}).\) Use symmetry to help locate the center of mass whenever possible.
20) [T] The region bounded by \(y=\cos(2x), \; x=−\frac{π}{4}\), and \(x=\frac{π}{4}\)
- Answer:
- \(\left(0,\frac{π}{8}\right)\)
21) [T] The region between \(y=2x^2, \; y=0, \; x=0,\) and \(x=1\)
22) [T] The region between \(y=\frac{5}{4}x^2\) and \(y=5\)
- Answer:
- \((0,3)\)
23) [T] Region between \(y=\sqrt{x}, \; y=\ln x, \; x=1,\) and \(x=4\)
24) [T] The region bounded by \(y=0\) and \(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
- Answer:
- \(\left(0,\frac{4}{π}\right)\)
25) [T] The region bounded by \(y=0, \; x=0,\) and \(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
26) [T] The region bounded by \(y=x^2\) and \(y=x^4\) in the first quadrant
- Answer:
- \(\left(\frac{5}{8},\, \frac{1}{3}\right)\)
In exercises 27 - 31, use the theorem of Pappus to determine the volume of the shape.
27) Rotating \(y=mx\) around the \(x\)-axis between \(x=0\) and \(x=1\)
28) Rotating \(y=mx\) around the \(y\)-axis between \(x=0\) and \(x=1\)
- Answer:
- \(V = \frac{mπ}{3}\) units³
29) A general cone created by rotating a triangle with vertices \((0,0), \, (a,0),\) and \((0,b)\) around the \(y\)-axis. Does your answer agree with the volume of a cone?
30) A general cylinder created by rotating a rectangle with vertices \((0,0), \, (a,0), \, (0,b),\) and \((a,b)\) around the \(y\)-axis. Does your answer agree with the volume of a cylinder?
- Answer:
- \(V = πa^2b\) units³
31) A sphere created by rotating a semicircle with radius \(a\) around the \(y\)-axis. Does your answer agree with the volume of a sphere?
In exercises 32 - 36, use a calculator to draw the region enclosed by the curve. Find the area \(M\) and the centroid \((\bar{x},\bar{y})\) for the given shapes. Use symmetry to help locate the center of mass whenever possible.
32) [T] Quarter-circle: \(y=\sqrt{1−x^2}, \; y=0\), and \(x=0\)
- Answer:
- \(\left(\frac{4}{3π},\, \frac{4}{3π}\right)\)
33) [T] Triangle: \(y=x, \; y=2−x\), and \(y=0\)
34) [T] Lens: \(y=x^2\) and \(y=x\)
- Answer:
- \(\left(\frac{1}{2},\, \frac{2}{5}\right)\)
35) [T] Ring: \(y^2+x^2=1\) and \(y^2+x^2=4\)
36) [T] Half-ring: \(y^2+x^2=1, \; y^2+x^2=4,\) and \(y=0\)
- Answer:
- \(\left(0,\, \frac{28}{9π}\right)\)
37) Find the generalized center of mass in the sliver between \(y=x^a\) and \(y=x^b\) with \(a>b\). Then, use the Pappus theorem to find the volume of the solid generated when revolving around the \(y\)-axis.
38) Find the generalized center of mass between \(y=a^2−x^2, \; x=0\), and \(y=0\). Then, use the Pappus theorem to find the volume of the solid generated when revolving around the \(y\)-axis.
- Answer:
- Center of mass: \(\left(\frac{a}{6},\,\frac{4a^2}{5}\right),\)
Volume: \(\dfrac{2πa^4}{9}\) units³
39) Find the generalized center of mass between \(y=b\sin(ax),\; x=0,\) and \(x=\dfrac{π}{a}.\) Then, use the Pappus theorem to find the volume of the solid generated when revolving around the \(y\)-axis.
40) Use the theorem of Pappus to find the volume of a torus (pictured here). Assume that a disk of radius \(a\) is positioned with the left end of the circle at \(x=b, \, b>0,\) and is rotated around the \(y\)-axis.
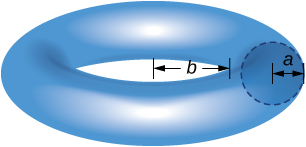
- Answer:
- Volume: \(V = 2\pi^2a^2(b+a)\)
41) Find the center of mass \((\bar{x},\bar{y})\) for a thin wire along the semicircle \(y=\sqrt{1−x^2}\) with unit mass. (Hint: Use the theorem of Pappus.)
6.7: Integrals, Exponential Functions, and Logarithms
In exercises 1 - 3, find the derivative \(\dfrac{dy}{dx}\).
1) \(y=\ln(2x)\)
- Answer:
- \(\dfrac{dy}{dx} = \dfrac{1}{x}\)
2) \(y=\ln(2x+1)\)
3) \(y=\dfrac{1}{\ln x}\)
- Answer:
- \(\dfrac{dy}{dx} = −\dfrac{1}{x(\ln x)^2}\)
In exercises 4 - 5, find the indefinite integral.
4) \(\displaystyle ∫\frac{dt}{3t}\)
5) \(\displaystyle ∫\frac{dx}{1+x}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{1+x} = \ln|x+1|+C\)
In exercises 6 - 15, find the derivative \(\dfrac{dy}{dx}.\) (You can use a calculator to plot the function and the derivative to confirm that it is correct.)
6) [T] \(y=\dfrac{\ln x}{x}\)
7) [T] \(y=x\ln x\)
- Answer:
- \(\dfrac{dy}{dx} = \ln(x)+1\)
8) [T] \(y=\log_{10}x\)
9) [T] \(y=\ln(\sin x)\)
- Answer:
- \(\dfrac{dy}{dx} = \cot x\)
10) [T] \(y=\ln(\ln x)\)
11) [T] \(y=7\ln(4x)\)
- Answer:
- \(\dfrac{dy}{dx} = \frac{7}{x}\)
12) [T] \(y=\ln\big((4x)^7\big)\)
13) [T] \(y=\ln(\tan x)\)
- Answer:
- \(\dfrac{dy}{dx} = \csc x\sec x\)
14) [T] \(y=\ln(\tan 3x)\)
15) [T] \(y=\ln(\cos^2x)\)
- Answer:
- \(\dfrac{dy}{dx} = −2\tan x\)
In exercises 16 - 25, find the definite or indefinite integral.
16) \(\displaystyle ∫^1_0\frac{dx}{3+x}\)
17) \(\displaystyle ∫^1_0\frac{dt}{3+2t}\)
- Answer:
- \(\displaystyle ∫^1_0\frac{dt}{3+2t} = \tfrac{1}{2}\ln\left(\tfrac{5}{3}\right)\)
18) \(\displaystyle ∫^2_0\frac{x}{x^2+1}\, dx\)
19) \(\displaystyle ∫^2_0\frac{x^3}{x^2+1}\,dx\)
- Answer:
- \(\displaystyle ∫^2_0\frac{x^3}{x^2+1}\,dx = 2−\tfrac{1}{2}\ln(5)\)
20) \(\displaystyle ∫^e_2\frac{dx}{x\ln x}\)
21) \(\displaystyle ∫^e_2\frac{dx}{(x\ln x)^2}\)
- Answer:
- \(\displaystyle ∫^e_2\frac{dx}{(x\ln x)^2} = \frac{1}{\ln(2)}−1\)
22) \(\displaystyle ∫\frac{\cos x}{\sin x}\, dx\)
23) \(\displaystyle ∫^{π/4}_0\tan x\,dx\)
- Answer:
- \(\displaystyle ∫^{π/4}_0\tan x\,dx = \tfrac{1}{2}\ln(2)\)
24) \(\displaystyle ∫\cot(3x)\,dx\)
25) \(\displaystyle ∫\frac{(\ln x)^2}{x}\, dx\)
- Answer:
- \(\displaystyle ∫\frac{(\ln x)^2}{x}\, dx = \tfrac{1}{3}(\ln x)^3\)
In exercises 26 - 35, compute \(\dfrac{dy}{dx}\) by differentiating \(\ln y\).
26) \(y=\sqrt{x^2+1}\)
27) \(y=\sqrt{x^2+1}\sqrt{x^2−1}\)
- Answer:
- \(\dfrac{dy}{dx} = \dfrac{2x^3}{\sqrt{x^2+1}\sqrt{x^2−1}}\)
28) \(y=e^{\sin x}\)
29) \(y=x^{−1/x}\)
- Answer:
- \(\dfrac{dy}{dx} = x^{−2−(1/x)}(\ln x−1)\)
30) \(y=e^{ex}\)
31) \(y=x^e\)
- Answer:
- \(\dfrac{dy}{dx} = ex^{e−1}\)
32) \(y=x^{(ex)}\)
33) \(y=\sqrt{x}\sqrt[3]{x}\sqrt[6]{x}\)
- Answer:
- \(\dfrac{dy}{dx} = 1\)
34) \(y=x^{−1/\ln x}\)
35) \(y=e^{−\ln x}\)
- Answer:
- \(\dfrac{dy}{dx} = −\dfrac{1}{x^2}\)
In exercises 36 - 40, evaluate by any method.
36) \(\displaystyle ∫^{10}_5\dfrac{dt}{t}−∫^{10x}_{5x}\dfrac{dt}{t}\)
37) \(\displaystyle ∫^{e^π}_1\dfrac{dx}{x}+∫^{−1}_{−2}\dfrac{dx}{x}\)
- Answer:
- \(π−\ln(2)\)
38) \(\dfrac{d}{dx}\left[\displaystyle ∫^1_x\dfrac{dt}{t}\right]\)
39) \(\dfrac{d}{dx}\left[\displaystyle ∫^{x^2}_x\dfrac{dt}{t}\right]\)
- Answer:
- \(\dfrac{1}{x}\)
40) \(\dfrac{d}{dx}\Big[\ln(\sec x+\tan x)\Big]\)
In exercises 41 - 44, use the function \(\ln x\). If you are unable to find intersection points analytically, use a calculator.
41) Find the area of the region enclosed by \(x=1\) and \(y=5\) above \(y=\ln x\).
- Answer:
- \((e^5−6)\text{ units}^2\)
42) [T] Find the arc length of \(\ln x\) from \(x=1\) to \(x=2\).
43) Find the area between \(\ln x\) and the \(x\)-axis from \(x=1\) to \(x=2\).
- Answer:
- \(\ln(4)−1) \text{ units}^2\)
44) Find the volume of the shape created when rotating this curve from \(x=1\) to \(x=2\) around the \(x\)-axis, as pictured here.
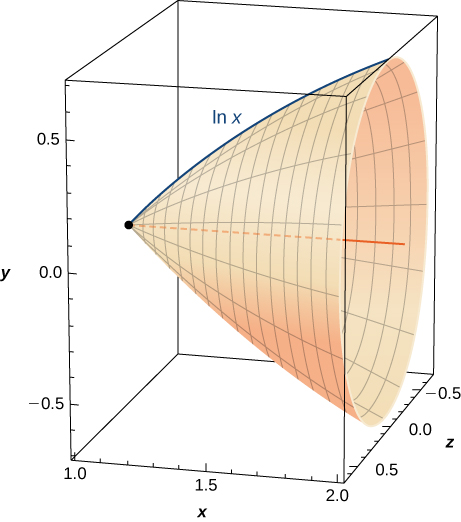
45) [T] Find the surface area of the shape created when rotating the curve in the previous exercise from \(x=1\) to \(x=2\) around the \(x\)-axis.
- Answer:
- \(2.8656 \text{ units}^2\)
If you are unable to find intersection points analytically in the following exercises, use a calculator.
46) Find the area of the hyperbolic quarter-circle enclosed by \(x=2\) and \(y=2\) above \(y=1/x.\)
47) [T] Find the arc length of \(y=1/x\) from \(x=1\) to \(x=4\).
- Answer:
- \(s = 3.1502\) units
48) Find the area under \(y=1/x\) and above the \(x\)-axis from \(x=1\) to \(x=4\).
In exercises 49 - 53, verify the derivatives and antiderivatives.
49) \(\dfrac{d}{dx}\Big[\ln(x+\sqrt{x^2+1})\Big]=\dfrac{1}{\sqrt{1+x^2}}\)
50) \(\dfrac{d}{dx}\Big[\ln\left(\frac{x−a}{x+a}\right)\Big]=\dfrac{2a}{(x^2−a^2)}\)
51) \(\dfrac{d}{dx}\Big[\ln\left(\frac{1+\sqrt{1−x^2}}{x}\right)\Big]=−\dfrac{1}{x\sqrt{1−x^2}}\)
52) \(\dfrac{d}{dx}\Big[\ln(x+\sqrt{x^2−a^2})\Big]=\dfrac{1}{\sqrt{x^2−a^2}}\)
53) \(\displaystyle ∫\frac{dx}{x\ln(x)\ln(\ln x)}=\ln|\ln(\ln x)|+C\)
6.8: Exponential Growth and Decay
In exercises 1 - 2, answer True or False? If true, prove it. If false, find the true answer.
1) The doubling time for \(y=e^{ct}\) is \(\dfrac{\ln 2}{\ln c}\).
2) If you invest \($500\), an annual rate of interest of \(3\%\) yields more money in the first year than a \(2.5\%\) continuous rate of interest.
- Answer:
- True
3) If you leave a \(100°C\) pot of tea at room temperature (\(25°C\)) and an identical pot in the refrigerator \((5°C)\), with \(k=0.02\), the tea in the refrigerator reaches a drinkable temperature \((70°C)\) more than \(5\) minutes before the tea at room temperature.
4) If given a half-life of t years, the constant \(k\) for \(y=e^{kt}\) is calculated by \(k=\frac{\ln\left(\frac{1}{2}\right)}{t}\).
- Answer:
- False; \(k=\dfrac{\ln 2}{t}\)
In exercises 5 - 18, use \(y=y_0e^{kt}.\)
5) If a culture of bacteria doubles in \(3\) hours, how many hours does it take to multiply by \(10\)?
6) If bacteria increase by a factor of \(10\) in \(10\) hours, how many hours does it take to increase by \(100\)?
- Answer:
- \(20\) hours
7) How old is a skull that contains one-fifth as much radiocarbon as a modern skull? Note that the half-life of radiocarbon is \(5730\) years.
8) If a relic contains \(90\%\) as much radiocarbon as new material, can it have come from the time of Christ (approximately \(2000\) years ago)? Note that the half-life of radiocarbon is \(5730\) years.
- Answer:
- No. The relic is approximately \(871\) years old.
9) The population of Cairo grew from \(5\) million to \(10\) million in \(20\) years. Use an exponential model to find when the population was \(8\) million.
10) The populations of New York and Los Angeles are growing at \(1\%\) and \(1.4\%\) a year, respectively. Starting from \(8\) million (New York) and \(6\) million (Los Angeles), when are the populations equal?
- Answer:
- \(71.92\) years
11) Suppose the value of \($1\) in Japanese yen decreases at \(2\%\) per year. Starting from \($1=¥250\), when will \($1=¥1\)?
12) The effect of advertising decays exponentially. If \(40\%\) of the population remembers a new product after \(3\) days, how long will \(20\%\)remember it?
- Answer:
- \(5\) days \(6\) hours \(27\)minutes
13) If \(y=1000\) at \(t=3\) and \(y=3000\) at \(t=4\), what was \(y_0\) at \(t=0\)?
14) If \(y=100\) at \(t=4\) and \(y=10\) at \(t=8\), when does \(y=1\)?
- Answer:
- At \(t = 12\)
15) If a bank offers annual interest of \(7.5\%\) or continuous interest of \(7.25\%,\) which has a better annual yield?
16) What continuous interest rate has the same yield as an annual rate of \(9\%\)?
- Answer:
- \(s = 3.1502\) units
Solution: \(8.618\%\)
17) If you deposit \($5000\)at \(8\%\) annual interest, how many years can you withdraw \($500\) (starting after the first year) without running out of money?
18) You are trying to save \($50,000\) in \(20\) years for college tuition for your child. If interest is a continuous \(10\%,\) how much do you need to invest initially?
- Answer:
- $6766.76
19) You are cooling a turkey that was taken out of the oven with an internal temperature of \(165°F\). After \(10\) minutes of resting the turkey in a \(70°F\) apartment, the temperature has reached \(155°F\). What is the temperature of the turkey \(20\) minutes after taking it out of the oven?
20) You are trying to thaw some vegetables that are at a temperature of \(1°F\). To thaw vegetables safely, you must put them in the refrigerator, which has an ambient temperature of \(44°F\). You check on your vegetables \(2\) hours after putting them in the refrigerator to find that they are now \(12°F\). Plot the resulting temperature curve and use it to determine when the vegetables reach \(33°\).
- Answer:
- \(9\)hours \(13\)minutes
21) You are an archeologist and are given a bone that is claimed to be from a Tyrannosaurus Rex. You know these dinosaurs lived during the Cretaceous Era (\(146\) million years to \(65\) million years ago), and you find by radiocarbon dating that there is \(0.000001\%\) the amount of radiocarbon. Is this bone from the Cretaceous?
22) The spent fuel of a nuclear reactor contains plutonium-239, which has a half-life of \(24,000\) years. If \(1\) barrel containing \(10\) kg of plutonium-239 is sealed, how many years must pass until only \(10\) g of plutonium-239 is left?
- Answer:
- \(239,179\) years
For exercises 23 - 26, use the following table, which features the world population by decade.
| Years since 1950 | Population (millions) |
| 0 | 2,556 |
| 10 | 3,039 |
| 20 | 3,706 |
| 30 | 4,453 |
| 40 | 5,279 |
| 50 | 6,083 |
| 60 | 6,849 |
Source: http:/www.factmonster.com/ipka/A0762181.html.
23) [T] The best-fit exponential curve to the data of the form \(P(t)=ae^{bt}\) is given by \(P(t)=2686e^{0.01604t}\). Use a graphing calculator to graph the data and the exponential curve together.
24) [T] Find and graph the derivative \(y′\) of your equation. Where is it increasing and what is the meaning of this increase?
- Answer:
- \(P'(t)=43e^{0.01604t}\). The population is always increasing.
25) [T] Find and graph the second derivative of your equation. Where is it increasing and what is the meaning of this increase?
26) [T] Find the predicted date when the population reaches \(10\) billion. Using your previous answers about the first and second derivatives, explain why exponential growth is unsuccessful in predicting the future.
- Answer:
- The population reaches \(10\) billion people in \(2027\).
For exercises 27 - 29, use the following table, which shows the population of San Francisco during the 19th century.
| Years since 1850 | Population (thousands) |
| 0 | 21.00 |
| 10 | 56.80 |
| 20 | 149.5 |
| 30 | 234.0 |
Source: http:/www.sfgenealogy.com/sf/history/hgpop.htm.
27) [T] The best-fit exponential curve to the data of the form \(P(t)=ae^{bt}\) is given by \(P(t)=35.26e^{0.06407t}\). Use a graphing calculator to graph the data and the exponential curve together.
28) [T] Find and graph the derivative \(y′\) of your equation. Where is it increasing? What is the meaning of this increase? Is there a value where the increase is maximal?
- Answer:
- \(P'(t)=2.259e^{0.06407t}\). The population is always increasing.
29) [T] Find and graph the second derivative of your equation. Where is it increasing? What is the meaning of this increase?
6.9: Calculus of the Hyperbolic Functions
Chapter Review Exercises
True or False? Justify your answer with a proof or a counterexample.
1) The amount of work to pump the water out of a half-full cylinder is half the amount of work to pump the water out of the full cylinder.
- Answer:
- False
2) If the force is constant, the amount of work to move an object from \(x=a\) to \(x=b\) is \(F(b−a)\).
3) The disk method can be used in any situation in which the washer method is successful at finding the volume of a solid of revolution.
- Answer:
- False
4) If the half-life of \(seaborgium-266\) is \(360\) ms, then \(k=(\ln(2))/360.\)
For exercises 5 - 8, use the requested method to determine the volume of the solid.
5) The volume that has a base of the ellipse \(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\) and cross-sections of an equilateral triangle perpendicular to the \(y\)-axis. Use the method of slicing.
- Answer:
- \(V = 32\sqrt{3}\, \text{units}^3\)
6) \(y=x^2−x\), from \(x=1\) to \(x=4\), rotated around the \(y\)-axis using the washer method
7) \(x=y^2\) and \(x=3y\) rotated around the \(y\)-axis using the washer method
- Answer:
- \(V = \frac{162π}{5}\, \text{units}^3\)
Solution:
8) \(x=2y^2−y^3,\; x=0\),and \(y=0\) rotated around the x-axis using cylindrical shells
For exercises 9 - 14, find
a. the area of the region,
b.the volume of the solid when rotated around the \(x\)-axis, and
c. the volume of the solid when rotated around the \(y\)-axis. Use whichever method seems most appropriate to you.
9) \(y=x^3,x=0,y=0\), and \(x=2\)
- Answer:
- a. \(A = 4\) units2
b. \(V = \frac{128π}{7}\) units3
c. \(V = \frac{64π}{5}\) units3
10) \(y=x^2−x\) and \(x=0\)
11) [T] \(y=\ln(x)+2\) and \(y=x\)
- Answer:
- a. \(A \approx 1.949\) units2
b. \(V \approx 21.952\) units3
c. \(V = \approx 17.099\) units3
12) \(y=x^2\) and \(y=\sqrt{x}\)
13) \(y=5+x, y=x^2, x=0\), and \(x=1\)
- Answer:
- a. \(A = \frac{31}{6}\) units2
b. \(V = \frac{452π}{15}\) units3
c. \(V = \frac{31π}{6}\) units3
14) Below \(x^2+y^2=1\) and above \(y=1−x\)
15) Find the mass of \(ρ=e^{−x}\) on a disk centered at the origin with radius \(4\).
- Answer:
- \(m \approx 245.282\)
16) Find the center of mass for \(ρ=\tan^2x\) on \(x∈(−\frac{π}{4},\frac{π}{4})\).
17) Find the mass and the center of mass of \(ρ=1\) on the region bounded by \(y=x^5\) and \(y=\sqrt{x}\).
- Answer:
- Mass: \(\frac{1}{2},\)
Center of mass: \((\frac{18}{35},\frac{9}{11})\)
For exercises 18 - 19, find the requested arc lengths.
18) The length of \(x\) for \(y=\cosh(x)\) from \(x=0\) to \(x=2\).
19) The length of \(y\) for \(x=3−\sqrt{y}\) from \(y=0\) to \(y=4\)
- Answer:
- \(s = \big[\sqrt{17}+\frac{1}{8}\ln(33+8\sqrt{17})\big]\) units
For exercises 20 - 21, find the surface area and volume when the given curves are revolved around the specified axis.
20) The shape created by revolving the region between \(y=4+x, \;y=3−x, \;x=0,\) and \(x=2\) rotated around the \(y\)-axis.
21) The loudspeaker created by revolving \(y=1/x\) from \(x=1\) to \(x=4\) around the \(x\)-axis.
- Answer:
- Volume: \(V = \frac{3π}{4}\) units3
Surface area: \(A = π\left(\sqrt{2}−\sinh^{−1}(1)+\sinh^{−1}(16)−\frac{\sqrt{257}}{16}\right)\) units2
For exercise 22, consider the Karun-3 dam in Iran. Its shape can be approximated as an isosceles triangle with height \(205\) m and width \(388\) m. Assume the current depth of the water is \(180\) m. The density of water is \(1000\) kg/m3.
22) Find the total force on the wall of the dam.
23) You are a crime scene investigator attempting to determine the time of death of a victim. It is noon and \(45\) °F outside and the temperature of the body is \(78\) °F. You know the cooling constant is \(k=0.00824\) °F/min. When did the victim die, assuming that a human’s temperature is \(98\) °F?
- Answer:
- 11:02 a.m.
For the following exercise, consider the stock market crash in 1929 in the United States. The table lists the Dow Jones industrial average per year leading up to the crash.
| Year after 1920 | Value ($) |
| 1 | 63.90 |
| 3 | 100 |
| 5 | 110 |
| 7 | 160 |
| 9 | 381.17 |
Source: http:/stockcharts.com/freecharts/hi...a19201940.html
24) [T] The best-fit exponential curve to these data is given by \(y=40.71+1.224^x\). Why do you think the gains of the market were unsustainable? Use first and second derivatives to help justify your answer. What would this model predict the Dow Jones industrial average to be in 2014 ?
For exercises 25 - 26, consider the catenoid, the only solid of revolution that has a minimal surface, or zero mean curvature. A catenoid in nature can be found when stretching soap between two rings.
25) Find the volume of the catenoid \(y=\cosh(x)\) from \(x=−1\) to \(x=1\) that is created by rotating this curve around the \(x\)-axis, as shown here.

- Answer:
- \(V = π\big(1+\sinh(1)\cosh(1)\big)\) units3
26) Find surface area of the catenoid \(y=\cosh(x)\) from \(x=−1\) to \(x=1\) that is created by rotating this curve around the \(x\)-axis.
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


