7.E: Techniques of Integration (Exercises)

7.1: Integration by Parts

In using the technique of integration by parts, you must carefully choose which expression is \(u\). For each of the following problems, use the guidelines in this section to choose \(u\). Do not evaluate the integrals.

1) \(\displaystyle ∫x^3e^{2x}\,dx\)

Answer

\( u=x^3\)

2) \(\displaystyle ∫x^3\ln(x)\,dx\)

3) \(\displaystyle ∫y^3\cos y\,dy\)

Answer

\(u=y^3\)

4) \(\displaystyle ∫x^2\arctan x\,dx\)

5) \(\displaystyle ∫e^{3x}\sin(2x)\,dx\)

Answer

\(u=\sin(2x)\)

In exercises 6 - 37, find the integral by using the simplest method. Not all problems require integration by parts.

6) \(\displaystyle ∫v\sin v\,dv\)

7) \(\displaystyle ∫\ln x\,dx\) (Hint: \(\displaystyle ∫\ln x\,dx\) is equivalent to \(\displaystyle ∫1⋅\ln(x)\,dx.)\)

Answer

\(\displaystyle ∫\ln x\,dx \quad = \quad−x+x\ln x+C\)

8) \(\displaystyle ∫x\cos x\,dx\)

9) \(\displaystyle ∫\tan^{−1}x\,dx\)

Answer

\(\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C\)

10) \(\displaystyle ∫x^2e^x\,dx\)

11) \(\displaystyle ∫x\sin(2x)\,dx\)

Answer

\(\displaystyle ∫x\sin(2x)\,dx \quad = \quad −\tfrac{1}{2}x\cos(2x)+\tfrac{1}{4}\sin(2x)+C\)

12) \(\displaystyle ∫xe^{4x}\,dx\)

13) \(\displaystyle ∫xe^{−x}\,dx\)

Answer

\(\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C\)

14) \(\displaystyle ∫x\cos 3x\,dx\)

15) \(\displaystyle ∫x^2\cos x\,dx\)

Answer

\(\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C\)

16) \(\displaystyle ∫x\ln x\,dx\)

17) \(\displaystyle ∫\ln(2x+1)\,dx\)

Answer

\(\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C\)

18) \(\displaystyle ∫x^2e^{4x}\,dx\)

19) \(\displaystyle ∫e^x\sin x\,dx\)

Answer

\(\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C\)

20) \(\displaystyle ∫e^x\cos x\,dx\)

21) \(\displaystyle ∫xe^{−x^2}\,dx\)

Answer

\(\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C\)

22) \(\displaystyle ∫x^2e^{−x}\,dx\)

23) \(\displaystyle ∫\sin(\ln(2x))\,dx\)

Answer

\(\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C\)

24) \(\displaystyle ∫\cos(\ln x)\,dx\)

25) \(\displaystyle ∫(\ln x)^2\,dx\)

Answer

\(\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C\)

26) \(\displaystyle ∫\ln(x^2)\,dx\)

27) \(\displaystyle ∫x^2\ln x\,dx\)

Answer

\(\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C\)

28) \(\displaystyle ∫\sin^{−1}x\,dx\)

29) \(\displaystyle ∫\cos^{−1}(2x)\,dx\)

Answer

\(\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C\)

30) \(\displaystyle ∫x\arctan x\,dx\)

31) \(\displaystyle ∫x^2\sin x\,dx\)

Answer

\(\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C\)

32) \(\displaystyle ∫x^3\cos x\,dx\)

33) \(\displaystyle ∫x^3\sin x\,dx\)

Answer

\(\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C\)

34) \(\displaystyle ∫x^3e^x\,dx\)

35) \(\displaystyle ∫x\sec^{−1}x\,dx\)

Answer

\(\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C\)

36) \(\displaystyle ∫x\sec^2x\,dx\)

37) \(\displaystyle ∫x\cosh x\,dx\)

Answer

\(\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C\)

In exercises 38 - 46, compute the definite integrals. Use a graphing utility to confirm your answers.

38) \(\displaystyle ∫^1_{1/e}\ln x\,dx\)

39) \(\displaystyle ∫^1_0xe^{−2x}\,dx\) (Express the answer in exact form.)

Answer

\(\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}\)

40) \(\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad (\text{let}\, u=\sqrt{x})\)

41) \(\displaystyle ∫^e_1\ln(x^2)\,dx\)

Answer

\(\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2\)

42) \(\displaystyle ∫^π_0x\cos x\,dx\)

43) \(\displaystyle ∫^π_{−π}x\sin x\,dx\) (Express the answer in exact form.)

Answer

\(\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi\)

44) \(\displaystyle ∫^3_0\ln(x^2+1)\,dx\) (Express the answer in exact form.)

45) \(\displaystyle ∫^{π/2}_0x^2\sin x\,dx\) (Express the answer in exact form.)

Answer

\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π\)

46) \(\displaystyle ∫^1_0x5^x\,dx\) (Express the answer using five significant digits.)

47) Evaluate \(\displaystyle ∫\cos x\ln(\sin x)\,dx\)

Answer

\(\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C\)

In exercises 48 - 50, derive the following formulas using the technique of integration by parts. Assume that \(n\) is a positive integer. These formulas are called reduction formulas because the exponent in the \(x\) term has been reduced by one in each case. The second integral is simpler than the original integral.

48) \(\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx\)

49) \(\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx\)

Answer

Answers vary

50) \(\displaystyle ∫x^n\sin x\,dx=\)______

51) Integrate \(\displaystyle ∫2x\sqrt{2x−3}\,dx\) using two methods:

a. Using parts, letting \(dv=\sqrt{2x−3}\,dx\)

b. Substitution, letting \(u=2x−3\)

Answer

a. \(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
b. \(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)

 

In exercises 52 - 57, state whether you would use integration by parts to evaluate the integral. If so, identify \(u\) and \(dv\). If not, describe the technique used to perform the integration without actually doing the problem.

52) \(\displaystyle ∫x\ln x\,dx\)

53) \(\displaystyle ∫\frac{\ln^2x}{x}\,dx\)

Answer

Do not use integration by parts. Choose \(u\) to be \(\ln x\), and the integral is of the form \(\displaystyle ∫u^2\,du.\)

54) \(\displaystyle ∫xe^x\,dx\)

55) \(\displaystyle ∫xe^{x^2−3}\,dx\)

Answer

Do not use integration by parts. Let \(u=x^2−3\), and the integral can be put into the form \(∫e^u\,du\).

56) \(\displaystyle ∫x^2\sin x\,dx\)

57) \(\displaystyle ∫x^2\sin(3x^3+2)\,dx\)

Answer

Do not use integration by parts. Choose \(u\) to be \(u=3x^3+2\) and the integral can be put into the form \(\displaystyle ∫\sin(u)\,du.\)

 

In exercises 58-59, sketch the region bounded above by the curve, the \(x\)-axis, and \(x=1\), and find the area of the region. Provide the exact form or round answers to the number of places indicated.

58) \(y=2xe^{−x}\) (Approximate answer to four decimal places.)

59) \(y=e^{−x}\sin(πx)\) (Approximate answer to five decimal places.)

Answer

The area under graph is \(0.39535 \, \text{units}^2.\)

 

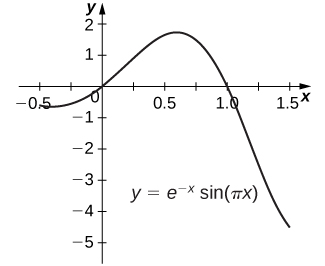
In exercises 60 - 61, find the volume generated by rotating the region bounded by the given curves about the specified line. Express the answers in exact form or approximate to the number of decimal places indicated.

60) \(y=\sin x,\,y=0,\,x=2π,\,x=3π;\) about the \(y\)-axis (Express the answer in exact form.)

61) \(y=e^{−x}, \,y=0,\,x=−1, \, x=0;\) about \(x=1\) (Express the answer in exact form.)

Answer

\(V = 2πe \, \text{units}^3\)

 

62) A particle moving along a straight line has a velocity of \(v(t)=t^2e^{−t}\) after \(t\) sec. How far does it travel in the first 2 sec? (Assume the units are in feet and express the answer in exact form.)

63) Find the area under the graph of \(y=\sec^3x\) from \(x=0\) to \(x=1\). (Round the answer to two significant digits.)

Answer

\(A= 2.05 \, \text{units}^2\)

64) Find the area between \(y=(x−2)e^x\) and the \(x\)-axis from \(x=2\) to \(x=5\). (Express the answer in exact form.)

65) Find the area of the region enclosed by the curve \(y=x\cos x\) and the \(x\)-axis for \(\frac{11π}{2}≤x≤\frac{13π}{2}.\) (Express the answer in exact form.)

Answer

\(A = 12π \, \text{units}^2\)

66) Find the volume of the solid generated by revolving the region bounded by the curve \(y=\ln x\), the \(x\)-axis, and the vertical line \(x=e^2\) about the \(x\)-axis. (Express the answer in exact form.)

67) Find the volume of the solid generated by revolving the region bounded by the curve \(y=4\cos x\) and the \(x\)-axis, \(\frac{π}{2}≤x≤\frac{3π}{2},\) about the \(x\)-axis. (Express the answer in exact form.)

Answer

\(V = 8π^2 \, \text{units}^3\)

68) Find the volume of the solid generated by revolving the region in the first quadrant bounded by \(y=e^x\) and the \(x\)-axis, from \(x=0\) to \(x=\ln(7)\), about the \(y\)-axis. (Express the answer in exact form.)

69) What is the volume of the Bundt cake that comes from rotating \( y=\sin x\) around the \(y\)-axis from \( x=0\) to \( x=π\)?

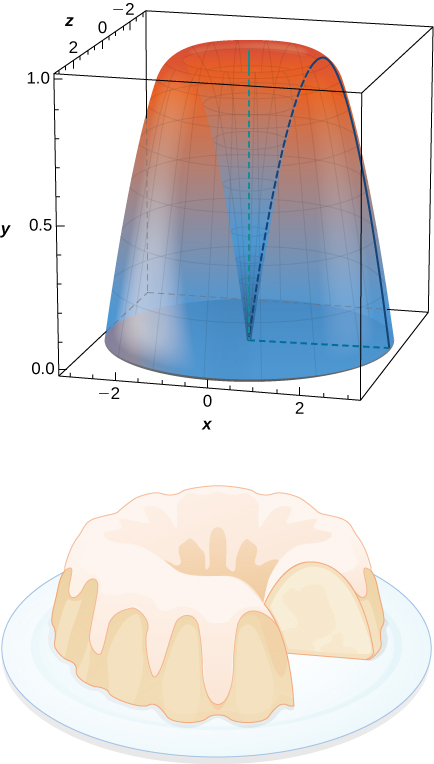
Answer

\(V = 2π^2\) units³

7.2: Trigonometric Integrals

Fill in the blank to make a true statement.

1) \(\sin^2x+\)_______\( =1\)

Answer

\(\cos^2x\)

2) \(\sec^2x−1=\)_______

Answer

\(\tan^2x\)

Use an identity to reduce the power of the trigonometric function to a trigonometric function raised to the first power.

3) \(\sin^2x=\)_______

Answer

\(\dfrac{1−\cos(2x)}{2}\)

4) \(\cos^2x=\)_______

Answer

\(\dfrac{1+\cos(2x)}{2}\)

 

Evaluate each of the following integrals by \(u\)-substitution.

5) \(\displaystyle ∫\sin^3x\cos x\,dx\)

Answer

\(\displaystyle ∫\sin^3x\cos x\,dx \quad = \quad \frac{\sin^4x}{4}+C\)

6) \(\displaystyle ∫\sqrt{\cos x}\sin x\,dx\)

7) \(\displaystyle ∫\tan^5(2x)\sec^2(2x)\,dx\)

Answer

\(\displaystyle ∫\tan^5(2x)\sec^2(2x)\,dx \quad = \quad \tfrac{1}{12}\tan^6(2x)+C\)

8) \(\displaystyle ∫\sin^7(2x)\cos(2x)\,dx\)

9) \(\displaystyle ∫\tan(\frac{x}{2})\sec^2(\frac{x}{2})\,dx\)

Answer

\(\displaystyle ∫\tan(\frac{x}{2})\sec^2(\frac{x}{2})\,dx \quad = \quad \tan^2(\frac{x}{2})+C\)

10) \(\displaystyle ∫\tan^2x\sec^2x\,dx\)

 

Compute the following integrals using the guidelines for integrating powers of trigonometric functions. Use a CAS to check the solutions. (Note: Some of the problems may be done using techniques of integration learned previously.)

11) \(\displaystyle ∫\sin^3x\,dx\)

Answer

\(\displaystyle ∫\sin^3x\,dx \quad = \quad −\frac{3\cos x}{4}+\tfrac{1}{12}\cos(3x)+C=−\cos x+\frac{\cos^3x}{3}+C\)

12) \(\displaystyle ∫\cos^3x\,dx\)

13) \(\displaystyle ∫\sin x\cos x\,dx\)

Answer

\(\displaystyle ∫\sin x\cos x\,dx \quad = \quad −\tfrac{1}{2}\cos^2x+C\)

14) \(\displaystyle ∫\cos^5x\,dx\)

15) \(\displaystyle ∫\sin^5x\cos^2x\,dx\)

Answer

\(\displaystyle ∫\sin^5x\cos^2x\,dx \quad = \quad −\frac{5\cos x}{64}−\tfrac{1}{192}\cos(3x)+\tfrac{3}{320}\cos(5x)−\tfrac{1}{448}\cos(7x)+C\)

16) \(\displaystyle ∫\sin^3x\cos^3x\,dx\)

17) \(\displaystyle ∫\sqrt{\sin x}\cos x\,dx\)

Answer

\(\displaystyle ∫\sqrt{\sin x}\cos x\,dx \quad = \quad \tfrac{2}{3}(\sin x)^{3/2}+C\)

18) \(\displaystyle ∫\sqrt{\sin x}\cos^3x\,dx\)

19) \(\displaystyle ∫\sec x\tan x\,dx\)

Answer

\(\displaystyle ∫\sec x\tan x\,dx \quad = \quad \sec x+C\)

20) \(\displaystyle ∫\tan(5x)\,dx\)

21) \(\displaystyle ∫\tan^2x\sec x\,dx\)

Answer

\(\displaystyle ∫\tan^2x\sec x\,dx \quad = \quad \tfrac{1}{2}\sec x\tan x−\tfrac{1}{2}\ln(\sec x+\tan x)+C\)

22) \(\displaystyle ∫\tan x\sec^3x\,dx\)

23) \(\displaystyle ∫\sec^4x\,dx\)

Answer

\(\displaystyle ∫\sec^4x\,dx \quad = \quad \frac{2\tan x}{3}+\tfrac{1}{3}\sec^2 x\tan x=\tan x+\frac{\tan^3x}{3}+C\)

24) \(\displaystyle ∫\cot x\,dx\)

25) \(\displaystyle ∫\csc x\,dx\)

Answer

\(\displaystyle ∫\csc x\,dx \quad = \quad −\ln|\cot x+\csc x|+C\)

26) \(\displaystyle ∫\frac{\tan^3x}{\sqrt{\sec x}}\,dx\)

 

For exercises 27 - 28, find a general formula for the integrals.

27) \(\displaystyle ∫\sin^2ax\cos ax\,dx\)

Answer

\(\displaystyle ∫\sin^2ax\cos ax\,dx \quad = \quad \frac{\sin^3(ax)}{3a}+C\)

28) \(\displaystyle ∫\sin ax\cos ax\,dx.\)

 

Use the double-angle formulas to evaluate the integrals in exercises 29 - 34.

29) \(\displaystyle ∫^π_0\sin^2x\,dx\)

Answer

\(\displaystyle ∫^π_0\sin^2x\,dx \quad = \quad \frac{π}{2}\)

30) \(\displaystyle ∫^π_0\sin^4 x\,dx\)

31) \(\displaystyle ∫\cos^2 3x\,dx\)

Answer

\(\displaystyle ∫\cos^2 3x\,dx \quad = \quad \frac{x}{2}+\tfrac{1}{12}\sin(6x)+C\)

32) \(\displaystyle ∫\sin^2x\cos^2x\,dx\)

33) \(\displaystyle ∫\sin^2x\,dx+∫\cos^2x\,dx\)

Answer

\(\displaystyle ∫\sin^2x\,dx+∫\cos^2x\,dx \quad = \quad x+C\)

34) \(\displaystyle ∫\sin^2 x\cos^2(2x)\,dx\)

 

For exercises 35 - 43, evaluate the definite integrals. Express answers in exact form whenever possible.

35) \(\displaystyle ∫^{2π}_0\cos x\sin 2x\,dx\)

Answer

\(\displaystyle ∫^{2π}_0\cos x\sin 2x\,dx \quad = \quad 0\)

36) \(\displaystyle ∫^π_0\sin 3x\sin 5x\,dx\)

37) \(\displaystyle ∫^π_0\cos(99x)\sin(101x)\,dx\)

Answer

\(\displaystyle ∫^π_0\cos(99x)\sin(101x)\,dx \quad = \quad 0\)

38) \(\displaystyle ∫^π_{−π}\cos^2(3x)\,dx\)

39) \(\displaystyle ∫^{2π}_0\sin x\sin(2x)\sin(3x)\,dx\)

Answer

\(\displaystyle ∫^{2π}_0\sin x\sin(2x)\sin(3x)\,dx \quad = \quad 0\)

40) \(\displaystyle ∫^{4π}_0\cos(x/2)\sin(x/2)\,dx\)

41) \(\displaystyle ∫^{π/3}_{π/6}\frac{\cos^3x}{\sqrt{\sin x}}\,dx\) (Round this answer to three decimal places.)

Answer

\(\displaystyle ∫^{π/3}_{π/6}\frac{\cos^3x}{\sqrt{\sin x}}\,dx \quad \approx \quad 0.239\)

42) \(\displaystyle ∫^{π/3}_{−π/3}\sqrt{\sec^2x−1}\,dx\)

43) \(\displaystyle ∫^{π/2}_0\sqrt{1−\cos(2x)}\,dx\)

Answer

\(\displaystyle ∫^{π/2}_0\sqrt{1−\cos(2x)}\,dx \quad = \quad \sqrt{2}\)

 

44) Find the area of the region bounded by the graphs of the equations \(y=\sin x,\, y=\sin^3x,\, x=0,\) and \(x=\frac{π}{2}.\)

45) Find the area of the region bounded by the graphs of the equations \(y=\cos^2x,\, y=\sin^2x,\, x=−\frac{π}{4},\) and \(x=\frac{π}{4}.\)

Answer

\(A = 1 \,\text{unit}^2\)

46) A particle moves in a straight line with the velocity function \(v(t)=\sin(ωt)\cos^2(ωt).\) Find its position function \(x=f(t)\) if \( f(0)=0.\)

47) Find the average value of the function \(f(x)=\sin^2x\cos^3x\) over the interval \([−π,π].\)

Answer

\(0\)

 

For exercises 48 - 49, solve the differential equations.

48) \(\dfrac{dy}{\,dx}=\sin^2x.\) The curve passes through point \((0,0).\)

49) \(\dfrac{dy}{dθ}=\sin^4(πθ)\)

Answer

\(f(x) = \dfrac{3θ}{8}−\tfrac{1}{4π}\sin(2πθ)+\tfrac{1}{32π}\sin(4πθ)+C\)

 

50) Find the length of the curve \(y=\ln(\csc x),\, \text{for}\,\tfrac{π}{4}≤x≤\tfrac{π}{2}.\)

51) Find the length of the curve \(y=\ln(\sin x),\, \text{for}\,\tfrac{π}{3}≤x≤\tfrac{π}{2}.\)

Answer

\(s = \ln(\sqrt{3})\)

52) Find the volume generated by revolving the curve \(y=\cos(3x)\) about the \(x\)-axis, for \( 0≤x≤\tfrac{π}{36}.\)

 

For exercises 53 - 54, use this information: The inner product of two functions \(f\) and \(g\) over \([a,b]\) is defined by \(\displaystyle f(x)⋅g(x)=⟨f,g⟩=∫^b_af⋅g\,dx.\) Two distinct functions \(f\) and \(g\) are said to be orthogonal if \(⟨f,g⟩=0.\)

53) Show that \({\sin(2x),\, \cos(3x)}\) are orthogonal over the interval \([−π,\, π]\).

Answer

\(\displaystyle ∫^π_{−π}\sin(2x)\cos(3x)\,dx=0\)

54) Evaluate \(\displaystyle ∫^π_{−π}\sin(mx)\cos(nx)\,dx.\)

 

55) Integrate \(y′=\sqrt{\tan x}\sec^4x.\)

Answer

\(\displaystyle y = \int \sqrt{\tan x}\sec^4x \, dx \quad = \quad \tfrac{2}{3}\left(\tan x\right)^{3/2} + \tfrac{2}{7}\left(\tan x\right)^{7/2}+C= \tfrac{2}{21}\left(\tan x\right)^{3/2}\left[ 7 + 3\tan^2 x \right]+C\)

 

For each pair of integrals in exercises 56 - 57, determine which one is more difficult to evaluate. Explain your reasoning.

56) \(\displaystyle ∫\sin^{456}x\cos x\,dx\) or \(\displaystyle ∫\sin^2x\cos^2x\,dx\)

57) \(\displaystyle ∫\tan^{350}x\sec^2x\,dx\) or \(\displaystyle ∫\tan^{350}x\sec x\,dx\)

Answer

The second integral is more difficult because the first integral is simply a \(u\)-substitution type.

 

7.3: Trigonometric Substitution

Simplify the expressions in exercises 1 - 5 by writing each one using a single trigonometric function.

1) \(4−4\sin^2θ\)

2) \(9\sec^2θ−9\)

Answer

\(9\sec^2θ−9 \quad = \quad 9\tan^2θ\)

3) \(a^2+a^2\tan^2θ\)

4) \(a^2+a^2\sinh^2θ\)

Answer

\(a^2+a^2\sinh^2θ \quad = \quad a^2\cosh^2θ\)

5) \(16\cosh^2θ−16\)

 

Use the technique of completing the square to express each trinomial in exercises 6 - 8 as the square of a binomial.

6) \(4x^2−4x+1\)

Answer

\( 4(x−\frac{1}{2})^2\)

7) \(2x^2−8x+3\)

8) \(−x^2−2x+4\)

Answer

\( −(x+1)^2+5\)

 

In exercises 9 - 28, integrate using the method of trigonometric substitution. Express the final answer in terms of the original variable.

9) \(\displaystyle ∫\frac{dx}{\sqrt{4−x^2}}\)

10) \(\displaystyle ∫\frac{dx}{\sqrt{x^2−a^2}}\)

Answer

\(\displaystyle ∫\frac{dx}{\sqrt{x^2−a^2}} \quad = \quad \ln∣x+\sqrt{−a^2+x^2}∣+C\)

11) \(\displaystyle ∫\sqrt{4−x^2}\,dx\)

12) \(\displaystyle ∫\frac{dx}{\sqrt{1+9x^2}}\)

Answer

\(\displaystyle ∫\frac{dx}{\sqrt{1+9x^2}} \quad = \quad \tfrac{1}{3}\ln∣\sqrt{9x^2+1}+3x∣+C\)

13) \(\displaystyle ∫\frac{x^2\,dx}{\sqrt{1−x^2}}\)

14) \(\displaystyle ∫\frac{dx}{x^2\sqrt{1−x^2}}\)

Answer

\(\displaystyle ∫\frac{dx}{x^2\sqrt{1−x^2}} \quad = \quad −\frac{\sqrt{1−x^2}}{x}+C\)

15) \(\displaystyle ∫\frac{dx}{(1+x^2)^2}\)

16) \(\displaystyle ∫\sqrt{x^2+9}\,dx\)

Answer

\(\displaystyle ∫\sqrt{x^2+9}\,dx \quad = \quad 9\left[\frac{x\sqrt{x^2+9}}{18}+\tfrac{1}{2}\ln\left|\frac{\sqrt{x^2+9}}{3}+\frac{x}{3}\right|\right]+C\)

17) \(\displaystyle ∫\frac{\sqrt{x^2−25}}{x}\,dx\)

18) \(\displaystyle ∫\frac{θ^3}{\sqrt{9−θ^2}}\,dθ\)

Answer

\(\displaystyle ∫\frac{θ^3dθ}{\sqrt{9−θ^2}}\,dθ \quad = \quad −\tfrac{1}{3}\sqrt{9−θ^2}(18+θ^2)+C\)

19) \(\displaystyle ∫\frac{dx}{\sqrt{x^6−x^2}}\)

20) \(\displaystyle ∫\sqrt{x^6−x^8}\,dx\)

Answer

\(\displaystyle ∫\sqrt{x^6−x^8}\,dx \quad = \quad \frac{(−1+x^2)(2+3x^2)\sqrt{x^6−x^8}}{15x^3}+C\)

21) \(\displaystyle ∫\frac{dx}{(1+x^2)^{3/2}}\)

22) \(\displaystyle ∫\frac{dx}{(x^2−9)^{3/2}}\)

Answer

\(\displaystyle ∫\frac{dx}{(x^2−9)^{3/2}} \quad = \quad −\frac{x}{9\sqrt{x^2-9}}+C\)

23) \(\displaystyle ∫\frac{\sqrt{1+x^2}}{x}\,dx\)

24) \(\displaystyle ∫\frac{x^2}{\sqrt{x^2−1}}\,dx\)

Answer

\(\displaystyle ∫\frac{x^2}{\sqrt{x^2−1}}\,dx \quad = \quad \tfrac{1}{2}(\ln∣x+\sqrt{x^2−1}∣+x\sqrt{x^2−1})+C\)

25) \(\displaystyle ∫\frac{x^2}{x^2+4}\,dx\)

26) \(\displaystyle ∫\frac{dx}{x^2\sqrt{x^2+1}}\)

Answer

\(\displaystyle ∫\frac{dx}{x^2\sqrt{x^2+1}} \quad = \quad −\frac{\sqrt{1+x^2}}{x}+C\)

27) \(\displaystyle ∫\frac{x^2}{\sqrt{1+x^2}}\,dx\)

28) \(\displaystyle ∫^1_{−1}(1−x^2)^{3/2}\,dx\)

Answer

\(\displaystyle ∫^1_{−1}(1−x^2)^{3/2}\,dx \quad = \quad \tfrac{1}{8}\left(x(5−2x^2)\sqrt{1−x^2}+3\arcsin x\right)+C\)

 

In exercises 29 - 34, use the substitutions \(x=\sinh θ, \, \cosh θ,\) or \(\tanh θ.\) Express the final answers in terms of the variable \(x\).

29) \(\displaystyle ∫\frac{dx}{\sqrt{x^2−1}}\)

30) \(\displaystyle ∫\frac{dx}{x\sqrt{1−x^2}}\)

Answer

\(\displaystyle ∫\frac{dx}{x\sqrt{1−x^2}} \quad = \quad \ln x−\ln∣1+\sqrt{1−x^2}∣+C\)

31) \(\displaystyle ∫\sqrt{x^2−1}\,dx\)

32) \(\displaystyle ∫\frac{\sqrt{x^2−1}}{x^2}\,dx\)

Answer

\(\displaystyle ∫\frac{\sqrt{x^2−1}}{x^2}\,dx \quad = \quad −\frac{\sqrt{−1+x^2}}{x}+\ln\left|x+\sqrt{−1+x^2}\right|+C\)

33) \(\displaystyle ∫\frac{dx}{1−x^2}\)

34) \(\displaystyle ∫\frac{\sqrt{1+x^2}}{x^2}\,dx\)

Answer

\(\displaystyle ∫\frac{\sqrt{1+x^2}}{x^2}\,dx \quad = \quad −\frac{\sqrt{1+x^2}}{x}+\text{arcsinh}\, x+C\)

 

Use the technique of completing the square to evaluate the integrals in exercises 35 - 39.

35) \(\displaystyle ∫\frac{1}{x^2−6x}\,dx\)

36) \(\displaystyle ∫\frac{1}{x^2+2x+1}\,dx\)

Answer

\(\displaystyle ∫\frac{1}{x^2+2x+1}\,dx \quad = \quad −\frac{1}{1+x}+C\)

37) \(\displaystyle ∫\frac{1}{\sqrt{−x^2+2x+8}}\,dx\)

38) \(\displaystyle ∫\frac{1}{\sqrt{−x^2+10x}}\,dx\)

Answer

\(\displaystyle ∫\frac{1}{\sqrt{−x^2+10x}}\,dx \quad = \quad \sin^{-1}\left(\frac{x-5}{5}\right)+C\)

39) \(\displaystyle ∫\frac{1}{\sqrt{x^2+4x−12}}\,dx\)

 

 

40) Evaluate the integral without using calculus: \(\displaystyle ∫^3_{−3}\sqrt{9−x^2}\,dx.\)

Answer

\(\displaystyle ∫^3_{−3}\sqrt{9−x^2}\,dx \quad = \quad \frac{9π}{2}\); area of a semicircle with radius 3

41) Find the area enclosed by the ellipse \(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1.\)

42) Evaluate the integral \(\displaystyle ∫\frac{dx}{\sqrt{1−x^2}}\) using two different substitutions. First, let \(x=\cos θ\) and evaluate using trigonometric substitution. Second, let \(x=\sin θ\) and use trigonometric substitution. Are the answers the same?

Answer

\(\displaystyle ∫\frac{dx}{\sqrt{1−x^2}} \quad = \quad \arcsin(x)+C\) is the common answer.

43) Evaluate the integral \(\displaystyle ∫\frac{dx}{x\sqrt{x^2−1}}\) using the substitution \(x=\sec θ\). Next, evaluate the same integral using the substitution \(x=\csc θ.\) Show that the results are equivalent.

44) Evaluate the integral \(\displaystyle ∫\frac{x}{x^2+1}\,dx\) using the form \(\displaystyle ∫\frac{1}{u}\,du\). Next, evaluate the same integral using \(x=\tan θ.\) Are the results the same?

Answer

\(\displaystyle ∫\frac{x}{x^2+1}\,dx \quad = \quad \frac{1}{2}\ln(1+x^2)+C\) is the result using either method.

45) State the method of integration you would use to evaluate the integral \(\displaystyle ∫x\sqrt{x^2+1}\,dx.\) Why did you choose this method?

46) State the method of integration you would use to evaluate the integral \(\displaystyle ∫x^2\sqrt{x^2−1}\,dx.\) Why did you choose this method?

Answer

Use trigonometric substitution. Let \(x=\sec(θ).\)

47) Evaluate \(\displaystyle ∫^1_{−1}\frac{x}{x^2+1}\,dx\)

48) Find the length of the arc of the curve over the specified interval: \(y=\ln x,\quad [1,5].\) Round the answer to three decimal places.

Answer

\( s = 4.367\) units

49) Find the surface area of the solid generated by revolving the region bounded by the graphs of \(y=x^2,\, y=0,\, x=0\), and \(x=\sqrt{2}\) about the \(x\)-axis. (Round the answer to three decimal places).

50) The region bounded by the graph of \(f(x)=\dfrac{1}{1+x^2}\) and the \(x\)-axis between \(x=0\) and \(x=1\) is revolved about the \(x\)-axis. Find the volume of the solid that is generated.

Answer

\( V = \left(\frac{π^2}{8}+\frac{π}{4}\right) \, \text{units}^3\)

 

In exercises 51 - 52, solve the initial-value problem for \(y\) as a function of \(x\).

51) \((x^2+36)\dfrac{dy}{dx}=1, \quad y(6)=0\)

52) \((64−x^2)\dfrac{dy}{dx}=1, \quad y(0)=3\)

Answer

\( y=\tfrac{1}{16}\ln\left|\dfrac{x+8}{x−8}\right|+3\)

 

53) Find the area bounded by \(y=\dfrac{2}{\sqrt{64−4x^2}},\, x=0,\, y=0\), and \(x=2\).

54) An oil storage tank can be described as the volume generated by revolving the area bounded by \(y=\dfrac{16}{\sqrt{64+x^2}},\, x=0,\, y=0,\, x=2\) about the \(x\)-axis. Find the volume of the tank (in cubic meters).

Answer

\(V = 24.6\) m³

55) During each cycle, the velocity \(v\) (in feet per second) of a robotic welding device is given by \(v=2t−\dfrac{14}{4+t^2}\), where \(t\) is time in seconds. Find the expression for the displacement \(s\) (in feet) as a function of \(t\) if \(s=0\) when \(t=0\).

56) Find the length of the curve \(y=\sqrt{16−x^2}\) between \(x=0\) and \(x=2\).

Answer

\( s = \frac{2π}{3}\) units

 

7.4: Partial Fractions

Use partial fraction decomposition (or a simpler technique) to express the rational function as a sum or difference of two or more simpler rational expressions.

1) \(\dfrac{1}{(x−3)(x−2)}\)

2) \(\dfrac{x^2+1}{x(x+1)(x+2)}\)

Answer

\(\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}\)

3) \(\dfrac{1}{x^3−x}\)

4) \(\dfrac{3x+1}{x^2}\)

Answer

\(\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}\)

5) \(\dfrac{3x^2}{x^2+1}\) (Hint: Use long division first.)

6) \(\dfrac{2x^4}{x^2−2x}\)

Answer

\(\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}\)

7) \(\dfrac{1}{(x−1)(x^2+1)}\)

8) \(\dfrac{1}{x^2(x−1)}\)

Answer

\(\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}\)

9) \(\dfrac{x}{x^2−4}\)

10) \(\dfrac{1}{x(x−1)(x−2)(x−3)}\)

Answer

\(\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}\)

11) \(\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}\)

12) \(\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}\)

Answer

\(\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}\)

13) \(\dfrac{2x}{(x+2)^2}\)

14) \(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}\)

Answer

\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}\)

 

In exercises 15 - 25, use the method of partial fractions to evaluate each of the following integrals.

15) \(\displaystyle ∫\frac{dx}{(x−3)(x−2)}\)

16) \(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx\)

Answer

\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C\)

17) \(\displaystyle ∫\frac{dx}{x^3−x}\)

18) \(\displaystyle ∫\frac{x}{x^2−4}\,dx\)

Answer

\(\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C\)

19) \(\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}\)

20) \(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx\)

Answer

\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C\)

21) \(\displaystyle ∫\frac{dx}{x^2−5x+6}\)

22) \(\displaystyle ∫\frac{2−x}{x^2+x}\,dx\)

Answer

\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C\)

23) \(\displaystyle ∫\frac{2}{x^2−x−6}\,dx\)

24) \(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}\)

Answer

\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C\)

25) \(\displaystyle ∫\frac{dx}{x^4−10x^2+9}\)

 

In exercises 26 - 29, evaluate the integrals with irreducible quadratic factors in the denominators.

26) \(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx\)

Answer

\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C\)

27) \(\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx\)

28) \(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx\)

Answer

\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C\)

29) \(\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx\)

 

In exercises 30 - 32, use the method of partial fractions to evaluate the integrals.

30) \(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx\)

Answer

\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C\)

31) \(\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx\)

32) \(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx\) (Hint: Use the rational root theorem.)

Answer

\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C\)

 

In exercises 33 - 46, use substitution to convert the integrals to integrals of rational functions. Then use partial fractions to evaluate the integrals.

33) \(\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx\) (Give the exact answer and the decimal equivalent. Round to five decimal places.)

34) \(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx\)

Answer

\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C\)

35) \(\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}\)

36) \(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx\)

Answer

\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C\)

37) \(\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx\)

38) \(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}\)

Answer

\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C\)

39) \(\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx\)

40) \(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}\)

Answer

\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C\)

41) \(\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}\)

42) \(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx\)

Answer

\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C\)

43) \(\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx\)

44) \(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx\)

Answer

\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}\)

45) \(\displaystyle ∫\frac{1}{2+e^{−x}}\,dx\)

46) \(\displaystyle ∫\frac{1}{1+e^x}\,dx\)

Answer

\(\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C\)

 

In exercises 47 - 48, use the given substitution to convert the integral to an integral of a rational function, then evaluate.

47) \(\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3\)

48) \(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6\)

Answer

\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C\)

 

49) Graph the curve \(y=\dfrac{x}{1+x}\) over the interval \([0,5]\). Then, find the area of the region bounded by the curve, the \(x\)-axis, and the line \(x=4\).

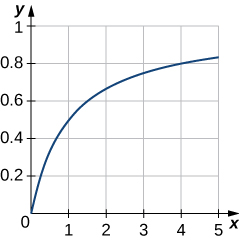
50) Find the volume of the solid generated when the region bounded by \(y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,\) and \(x=2\) is revolved about the \(x\)-axis.

Answer

\(V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3\)

51) The velocity of a particle moving along a line is a function of time given by \(v(t)=\dfrac{88t^2}{t^2+1}.\) Find the distance that the particle has traveled after \(t=5\) sec.

In exercises 52 - 54, solve the initial-value problem for \(x\) as a function of \(t\).

52) \((t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0\)

Answer

\( x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|\)

53) \((t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1\)

54) \((2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0\)

Answer

\(x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5\)

55) Find the \(x\)-coordinate of the centroid of the area bounded by \(y(x^2−9)=1, \, y=0, \,x=4,\) and \(x=5.\) (Round the answer to two decimal places.)

56) Find the volume generated by revolving the area bounded by \(y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7\), and \(y=0\) about the \(y\)-axis.

Answer

\(V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3\)

57) Find the area bounded by \(y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,\) and \(x=4\). (Round the answer to the nearest hundredth.)

58) Evaluate the integral \(\displaystyle ∫\frac{dx}{x^3+1}.\)

Answer

\(\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C\)

For problems 59 - 62, use the substitutions \(\tan(\frac{x}{2})=t, \,dx=\dfrac{2}{1+t^2}\,dt, \, \sin x=\dfrac{2t}{1+t^2},\) and \(\cos x=\dfrac{1−t^2}{1+t^2}.\)

59) \(\displaystyle ∫\frac{dx}{3−5\sin x}\)

60) Find the area under the curve \(y=\dfrac{1}{1+\sin x}\) between \(x=0\) and \(x=π.\) (Assume the dimensions are in inches.)

Answer

2.0 in.²

61) Given \(\tan(\frac{x}{2})=t,\) derive the formulas \(dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}\), and \(\cos x=\dfrac{1−t^2}{1+t^2}.\)

62) Evaluate \(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.\)

Answer

\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C\)

7.5: Other Strategies for Integration

Use a table of integrals to evaluate the following integrals.

1) \(\displaystyle ∫_0^4\frac{x}{\sqrt{1+2x}}\,dx\)

2) \(\displaystyle ∫\frac{x+3}{x^2+2x+2}\,dx\)

Answer

\(\displaystyle ∫\frac{x+3}{x^2+2x+2}\,dx = \tfrac{1}{2}\ln |x^2+2x+2|+2\arctan(x+1)+C\)

3) \(\displaystyle ∫x^3\sqrt{1+2x^2}\,dx\)

4) \(\displaystyle ∫\frac{1}{\sqrt{x^2+6x}}\,dx\)

Answer

\(\displaystyle ∫\frac{1}{\sqrt{x^2+6x}}\,dx = \cosh^{−1}\left(\frac{x+3}{3}\right)+C\)

5) \(\displaystyle ∫\frac{x}{x+1}\,dx\)

6) \(\displaystyle ∫x⋅2^{x^2}\,dx\)

Answer

\(\displaystyle ∫x⋅2^{x^2}\,dx = \frac{2^{x^2−1}}{\ln 2}+C\)

7) \(\displaystyle ∫\frac{1}{4x^2+25}\,dx\)

8) \(\displaystyle ∫\frac{dy}{\sqrt{4−y^2}}\)

Answer

\(\displaystyle ∫\frac{dy}{\sqrt{4−y^2}} = \arcsin\left(\frac{y}{2}\right)+C\)

9) \(\displaystyle ∫\sin^3(2x)\cos(2x)\,dx\)

10) \(\displaystyle ∫\csc(2w)\cot(2w)\,dw\)

Answer

\(\displaystyle ∫\csc(2w)\cot(2w)\,dw = −\tfrac{1}{2}\csc(2w)+C\)

11) \(\displaystyle ∫2^y\,dy\)

12) \(\displaystyle ∫^1_0\frac{3x}{\sqrt{x^2+8}}\,dx\)

Answer

\(\displaystyle ∫^1_0\frac{3x}{\sqrt{x^2+8}}\,dx = 9−6\sqrt{2}\)

13) \(\displaystyle ∫^{1/4}_{−1/4}\sec^2(πx)\tan(πx)\,dx\)

14) \(\displaystyle ∫^{π/2}_0\tan^2\left(\frac{x}{2}\right)\,dx\)

Answer

\(\displaystyle ∫^{π/2}_0\tan^2\left(\frac{x}{2}\right)\,dx = 2−\frac{π}{2}\)

15) \(\displaystyle ∫\cos^3x\,dx\)

16) \(\displaystyle ∫\tan^5(3x)\,dx\)

Answer

\(\displaystyle ∫\tan^5(3x)\,dx = \tfrac{1}{12}\tan^4(3x)−\tfrac{1}{6}\tan^2(3x)+\tfrac{1}{3}\ln|\sec 3x|+C\)

17) \(\displaystyle ∫\sin^2y\cos^3y\,dy\)

Use a CAS to evaluate the following integrals. Tables can also be used to verify the answers.

18) [T] \(\displaystyle ∫\frac{dw}{1+\sec\left(\frac{w}{2}\right)}\)

Answer

\(\displaystyle ∫\frac{dw}{1+\sec\left(\frac{w}{2}\right)} = 2\cot\left(\tfrac{w}{2}\right)−2\csc\left(\tfrac{w}{2}\right)+w+C\)

19) [T] \(\displaystyle ∫\frac{dw}{1−\cos(7w)}\)

20) [T] \(\displaystyle ∫^t_0\frac{dt}{4\cos t+3\sin t}\)

Answer

\(\displaystyle ∫^t_0\frac{dt}{4\cos t+3\sin t} = \tfrac{1}{5}\ln\Big|\frac{2(5+4\sin t−3\cos t)}{4\cos t+3\sin t}\Big|\)

21) [T] \(\displaystyle ∫\frac{\sqrt{x^2−9}}{3x}\,dx\)

22) [T] \(\displaystyle ∫\frac{dx}{x^{1/2}+x^{1/3}}\)

Answer

\(\displaystyle ∫\frac{dx}{x^{1/2}+x^{1/3}} = 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln[1+x^{1/6}]+C\)

23) [T] \(\displaystyle ∫\frac{dx}{x\sqrt{x−1}}\)

24) [T] \(\displaystyle ∫x^3\sin x\,dx\)

Answer

\(\displaystyle ∫x^3\sin x\,dx = −x^3\cos x+3x^2\sin x+6x\cos x−6\sin x+C\)

25) [T] \(\displaystyle ∫x\sqrt{x^4−9}\,dx\)

26) [T] \(\displaystyle ∫\frac{x}{1+e^{−x^2}}\,dx\)

Answer

\(\displaystyle ∫\frac{x}{1+e^{−x^2}}\,dx = \tfrac{1}{2}\left(x^2+\ln|1+e^{−x^2}|\right)+C\)

27) [T] \(\displaystyle ∫\frac{\sqrt{3−5x}}{2x}\,dx\)

28) [T] \(\displaystyle ∫\frac{dx}{x\sqrt{x−1}}\)

Answer

\(\displaystyle ∫\frac{dx}{x\sqrt{x−1}} = 2\arctan\big(\sqrt{x−1}\big)+C\)

29) [T] \(\displaystyle ∫e^x\cos^{−1}(e^x)\,dx\)

Use a calculator or CAS to evaluate the following integrals.

30) [T] \(\displaystyle ∫^{π/4}_0\cos 2x \, dx\)

Answer

\(\displaystyle ∫^{π/4}_0\cos 2x \, dx = 0.5=\frac{1}{2}\)

31) [T] \(\displaystyle ∫^1_0x⋅e^{−x^2}\,dx\)

32) [T] \(\displaystyle ∫^8_0\frac{2x}{\sqrt{x^2+36}}\,dx\)

Answer

\(\displaystyle ∫^8_0\frac{2x}{\sqrt{x^2+36}}\,dx = 8.0\)

33) [T] \(\displaystyle ∫^{2/\sqrt{3}}_0\frac{1}{4+9x^2}\,dx\)

34) [T] \(\displaystyle ∫\frac{dx}{x^2+4x+13}\)

Answer

\(\displaystyle ∫\frac{dx}{x^2+4x+13} = \tfrac{1}{3}\arctan\left(\tfrac{1}{3}(x+2)\right)+C\)

35) [T] \(\displaystyle ∫\frac{dx}{1+\sin x}\)

Use tables to evaluate the integrals. You may need to complete the square or change variables to put the integral into a form given in the table.

36) \(\displaystyle ∫\frac{dx}{x^2+2x+10}\)

Answer

\(\displaystyle ∫\frac{dx}{x^2+2x+10} = \tfrac{1}{3}\arctan\left(\frac{x+1}{3}\right)+C\)

37) \(\displaystyle ∫\frac{dx}{\sqrt{x^2−6x}}\)

38) \(\displaystyle ∫\frac{e^x}{\sqrt{e^{2x}−4}}\,dx\)

Answer

\(\displaystyle ∫\frac{e^x}{\sqrt{e^{2x}−4}}\,dx = \ln\left(e^x+\sqrt{4+e^{2x}}\right)+C\)

39) \(\displaystyle ∫\frac{\cos x}{\sin^2x+2\sin x}\,dx\)

40) \(\displaystyle ∫\frac{\arctan(x^3)}{x^4}\,dx\)

Answer

\(\displaystyle ∫\frac{\arctan(x^3)}{x^4}\,dx = \ln x−\tfrac{1}{6}\ln(x^6+1)−\frac{\arctan(x^3)}{3x^3}+C\)

41) \(\displaystyle ∫\frac{\ln|x|\arcsin\left(\ln|x|\right)}{x}\,dx\)

Use tables to perform the integration.

42) \(\displaystyle ∫\frac{dx}{\sqrt{x^2+16}}\)

Answer

\(\displaystyle ∫\frac{dx}{\sqrt{x^2+16}} = \ln |x|+\sqrt{16+x^2}∣+C\)

43) \(\displaystyle ∫\frac{3x}{2x+7}\,dx\)

44) \(\displaystyle ∫\frac{dx}{1−\cos 4x}\)

Answer

\(\displaystyle ∫\frac{dx}{1−\cos 4x} = −\frac{1}{4}\cot 2x+C\)

45) \(\displaystyle ∫\frac{dx}{\sqrt{4x+1}}\)

46) Find the area bounded by \(y(4+25x^2)=5,\;x=0,\;y=0,\) and \(x=4.\) Use a table of integrals or a CAS.

Answer

\(\frac{1}{2}\arctan 10\) units²

47) The region bounded between the curve \(y=\dfrac{1}{\sqrt{1+\cos x}}, \; 0.3≤x≤1.1,\) and the \(x\)-axis is revolved about the \(x\)-axis to generate a solid. Use a table of integrals to find the volume of the solid generated. (Round the answer to two decimal places.)

48) Use substitution and a table of integrals to find the area of the surface generated by revolving the curve \(y=e^x,\; 0≤x≤3,\) about the \(x\)-axis. (Round the answer to two decimal places.)

Answer

\(1276.14\) units²

49) [T] Use an integral table and a calculator to find the area of the surface generated by revolving the curve \(y=\dfrac{x^2}{2},\; 0≤x≤1,\) about the \(x\)-axis. (Round the answer to two decimal places.)

50) [T] Use a CAS or tables to find the area of the surface generated by revolving the curve \(y=\cos x,\; 0≤x≤\frac{π}{2},\) about the \(x\)-axis. (Round the answer to two decimal places.)

Answer

\(7.21\) units²

51) Find the length of the curve \(y=\dfrac{x^2}{4}\) over \([0,8]\).

52) Find the length of the curve \(y=e^x\) over \([0,\,\ln(2)].\)

Answer

\(\left(\sqrt{5}−\sqrt{2}+\ln\Big|\frac{2+2\sqrt{2}}{1+\sqrt{5}}\Big|\right)\) units

53) Find the area of the surface formed by revolving the graph of \(y=2\sqrt{x}\) over the interval \([0,9]\) about the \(x\)-axis.

54) Find the average value of the function \(f(x)=\dfrac{1}{x^2+1}\) over the interval \([−3,3].\)

Answer

\(\frac{1}{3}\arctan(3)≈0.416\)

55) Approximate the arc length of the curve \(y=\tan πx\) over the interval \(\left[0,\frac{1}{4}\right]\). (Round the answer to three decimal places.)

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

7.6: Numerical Integration

In exercises 1 - 5, approximate the following integrals using either the midpoint rule, trapezoidal rule, or Simpson’s rule as indicated. (Round answers to three decimal places.)

1) \( \displaystyle ∫^2_1\frac{dx}{x};\) trapezoidal rule; \( n=5\)

Answer

\( 0.696\)

2) \( \displaystyle ∫^3_0\sqrt{4+x^3}\;dx;\) trapezoidal rule; \( n=6\)

3) \( \displaystyle ∫^3_0\sqrt{4+x^3}\;dx;\) Simpson’s rule; \( n=6\)

Answer

\( 9.279\)

4) \( \displaystyle ∫^{12}_0x^2\;dx;\) midpoint rule; \( n=6\)

5) \( \displaystyle ∫^1_0\sin^2(\pi x)\;dx;\) midpoint rule; \( n=3\)

Answer

\( 0.500\)

 

6) Use the midpoint rule with eight subdivisions to estimate \( \displaystyle ∫^4_2x^2\;dx.\)

7) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^4_2x^2\;dx.\)

Answer

\( T_4=18.75\)

8) Find the exact value of \( \displaystyle ∫^4_2x^2\;dx.\) Find the error of approximation between the exact value and the value calculated using the trapezoidal rule with four subdivisions. Draw a graph to illustrate.

 

Approximate the integral to four decimal places using the indicated rule.

9) \( \displaystyle ∫^1_0\sin^2(\pi x)\;dx;\) trapezoidal rule; \( n=6\)

Answer

\( 0.5000\)

10) \( \displaystyle ∫^3_0\frac{1}{1+x^3}\;dx;\) trapezoidal rule; \( n=6\)

11) \( \displaystyle ∫^3_0\frac{1}{1+x^3}\;dx;\) Simpson’s rule; \( n=6\)

Answer

\( 1.1614\)

12) \( \displaystyle ∫^{0.8}_0e^{−x^2}\;dx;\) trapezoidal rule; \( n=4\)

13) \( \displaystyle ∫^{0.8}_0e^{−x^2}\;dx;\) Simpson’s rule; \( n=4\)

Answer

\(0.6577\)

14) \(\displaystyle ∫^{0.4}_0\sin(x^2)\;dx;\) trapezoidal rule; \( n=4\)

15) \(\displaystyle ∫^{0.4}_0\sin(x^2)\;dx;\) Simpson’s rule; \( n=4\)

Answer

\(0.0213\)

16) \( \displaystyle ∫^{0.5}_{0.1}\frac{\cos x}{x}\;dx;\) trapezoidal rule; \(n=4\)

17) \( \displaystyle ∫^{0.5}_{0.1}\frac{\cos x}{x}\;dx;\) Simpson’s rule; \(n=4\)

Answer

\(1.5629\)

18) Evaluate \( \displaystyle ∫^1_0\frac{dx}{1+x^2}\) exactly and show that the result is \( π/4\). Then, find the approximate value of the integral using the trapezoidal rule with \( n=4\) subdivisions. Use the result to approximate the value of \( π\).

19) Approximate \( \displaystyle ∫^4_2\frac{1}{\ln x}\;dx\) using the midpoint rule with four subdivisions to four decimal places.

Answer

\( 1.9133\)

20) Approximate \( \displaystyle ∫^4_2\frac{1}{\ln x}\;dx\) using the trapezoidal rule with eight subdivisions to four decimal places.

21) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^{0.8}_0x^3\;dx\) to four decimal places.

Answer

\( T(4)=0.1088\)

22) Use the trapezoidal rule with four subdivisions to estimate \( \displaystyle ∫^{0.8}_0x^3\;dx.\) Compare this value with the exact value and find the error estimate.

23) Using Simpson’s rule with four subdivisions, find \( \displaystyle ∫^{π/2}_0\cos(x)\;dx.\)

Answer

\( \displaystyle ∫^{π/2}_0\cos(x)\;dx\approx \quad 1.0\)

24) Show that the exact value of \( \displaystyle ∫^1_0xe^{−x}\;dx=1−\frac{2}{e}\). Find the absolute error if you approximate the integral using the midpoint rule with 16 subdivisions.

25) Given \( \displaystyle ∫^1_0xe^{−x}\;dx=1−\frac{2}{e},\) use the trapezoidal rule with 16 subdivisions to approximate the integral and find the absolute error.

Answer

Approximate error is \( 0.000325.\)

26) Find an upper bound for the error in estimating \( \displaystyle ∫^3_0(5x+4)\;dx\) using the trapezoidal rule with six steps.

27) Find an upper bound for the error in estimating \( \displaystyle ∫^5_4\frac{1}{(x−1)^2}\;dx\) using the trapezoidal rule with seven subdivisions.

Answer

\( \frac{1}{7938}\)

28) Find an upper bound for the error in estimating \( \displaystyle ∫^3_0(6x^2−1)\;dx\) using Simpson’s rule with \( n=10\) steps.

29) Find an upper bound for the error in estimating \( \displaystyle ∫^5_2\frac{1}{x−1}\;dx\) using Simpson’s rule with \( n=10\) steps.

Answer

\( \frac{81}{25,000}\)

30) Find an upper bound for the error in estimating \( \displaystyle ∫^π_02x\cos(x)\;dx\) using Simpson’s rule with four steps.

31) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^4_1(5x^2+8)\;dx\) with an error magnitude of less than 0.0001 using the trapezoidal rule.

Answer

\( 475\)

32) Determine a value of n such that the trapezoidal rule will approximate \( \displaystyle ∫^1_0\sqrt{1+x^2}\;dx\) with an error of no more than 0.01.

33) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^3_2(2x^3+4x)\;dx\) with an error of magnitude less than 0.0001 using the trapezoidal rule.

Answer

\( 174\)

34) Estimate the minimum number of subintervals needed to approximate the integral \( \displaystyle ∫^4_3\frac{1}{(x−1)^2}\;dx\) with an error magnitude of less than 0.0001 using the trapezoidal rule.

35) Use Simpson’s rule with four subdivisions to approximate the area under the probability density function \( y=\frac{1}{\sqrt{2π}}e^{−x^2/2}\) from \( x=0\) to \( x=0.4\).

Answer

\( 0.1544\)

36) Use Simpson’s rule with \( n=14\) to approximate (to three decimal places) the area of the region bounded by the graphs of \( y=0, x=0,\) and \( x=π/2.\)

37) The length of one arch of the curve \( y=3\sin(2x)\) is given by \( L=∫^{π/2}_0\sqrt{1+36\cos^2(2x)}\;dx.\) Estimate L using the trapezoidal rule with \( n=6\).

Answer

\( 6.2807\)

38) The length of the ellipse \( x=a\cos(t),y=b\sin(t),0≤t≤2π\) is given by \( L=4a∫^{π/2}_0\sqrt{1−e^2\cos^2(t)}dt\), where e is the eccentricity of the ellipse. Use Simpson’s rule with \( n=6\) subdivisions to estimate the length of the ellipse when \( a=2\) and \( e=1/3.\)

39) Estimate the area of the surface generated by revolving the curve \( y=\cos(2x),0≤x≤\frac{π}{4}\) about the x-axis. Use the trapezoidal rule with six subdivisions.

Answer

\( 4.606\)

40) Estimate the area of the surface generated by revolving the curve \( y=2x^2, 0≤x≤3\) about the x-axis. Use Simpson’s rule with \( n=6.\)

41) The growth rate of a certain tree (in feet) is given by \( y=\dfrac{2}{t+1}+e^{−t^2/2},\) where t is time in years. Estimate the growth of the tree through the end of the second year by using Simpson’s rule, using two subintervals. (Round the answer to the nearest hundredth.)

Answer

\( 3.41\) ft

42) [T] Use a calculator to approximate \( \displaystyle ∫^1_0\sin(πx)\;dx\) using the midpoint rule with 25 subdivisions. Compute the relative error of approximation.

43) [T] Given \( \displaystyle ∫^5_1(3x^2−2x)\;dx=100,\) approximate the value of this integral using the midpoint rule with 16 subdivisions and determine the absolute error.

Answer

\( T_{16}=100.125;\) absolute error = \( 0.125\)

44) Given that we know the Fundamental Theorem of Calculus, why would we want to develop numerical methods for definite integrals?

45) The table represents the coordinates \( (x,​y)\) that give the boundary of a lot. The units of measurement are meters. Use the trapezoidal rule to estimate the number of square meters of land that is in this lot.

\( x\)	\( y\)	\( x\)	\( y\)
0	125	600	95
100	125	700	88
200	120	800	75
300	112	900	35
400	90	1000	0
500	90

Answer

about 89,250 m²

46) Choose the correct answer. When Simpson’s rule is used to approximate the definite integral, it is necessary that the number of partitions be____

a. an even number

b. odd number

c. either an even or an odd number

d. a multiple of 4

47) The “Simpson” sum is based on the area under a ____.

Answer

parabola

48) The error formula for Simpson’s rule depends on___.

a. \( f(x)\)

b. \( f′(x)\)

c. \( f^{(4)}(x)\)

d. the number of steps

7.7: Improper Integrals

In exercises 1 - 8, evaluate the following integrals. If the integral is not convergent, answer “It diverges.”

1) \(\displaystyle ∫^4_2\frac{dx}{(x−3)^2}\)

Answer

It diverges.

2) \(\displaystyle ∫^∞_0\frac{1}{4+x^2}\,dx\)

3) \(\displaystyle ∫^2_0\frac{1}{\sqrt{4−x^2}}\,dx\)

Answer

Converges to \(\frac{π}{2}\)

4) \(\displaystyle ∫^∞_1\frac{1}{x\ln x}\,dx\)

5) \(\displaystyle ∫^∞_1xe^{−x}\,dx\)

Answer

Converges to \(\frac{2}{e}\)

6) \(\displaystyle ∫^∞_{−∞}\frac{x}{x^2+1}\,dx\)

7) Without integrating, determine whether the integral \(\displaystyle ∫^∞_1\frac{1}{\sqrt{x^3+1}}\,dx\) converges or diverges by comparing the function \(f(x)=\dfrac{1}{\sqrt{x^3+1}}\) with \(g(x)=\dfrac{1}{\sqrt{x^3}}\).

Answer

It converges.

8) Without integrating, determine whether the integral \(\displaystyle ∫^∞_1\frac{1}{\sqrt{x+1}}\,dx\) converges or diverges.

 

In exercises 9 - 25, determine whether the improper integrals converge or diverge. If possible, determine the value of the integrals that converge.

9) \(\displaystyle ∫^∞_0e^{−x}\cos x\,dx\)

Answer

Converges to \(\frac{1}{2}\).

10) \(\displaystyle ∫^∞_1\frac{\ln x}{x}\,dx\)

11) \(\displaystyle ∫^1_0\frac{\ln x}{\sqrt{x}}\,dx\)

Answer

Converges to \(-4\).

12) \(\displaystyle ∫^1_0\ln x\,dx\)

13) \(\displaystyle ∫^∞_{−∞}\frac{1}{x^2+1}\,dx\)

Answer

Converges to \(π\).

14) \(\displaystyle ∫^5_1\frac{dx}{\sqrt{x−1}}\)

15) \(\displaystyle ∫^2_{−2}\frac{dx}{(1+x)^2}\)

Answer

It diverges.

16) \(\displaystyle ∫^∞_0e^{−x}\,dx\)

17) \(\displaystyle ∫^∞_0\sin x\,dx\)

Answer

It diverges.

18) \(\displaystyle ∫^∞_{−∞}\frac{e^x}{1+e^{2x}}\,dx\)

19) \(\displaystyle ∫^1_0\frac{dx}{\sqrt[3]{x}}\)

Answer

Converges to \(1.5\).

20) \(\displaystyle ∫^2_0\frac{dx}{x^3}\)

21) \(\displaystyle ∫^2_{−1}\frac{dx}{x^3}\)

Answer

It diverges.

22) \(\displaystyle ∫^1_0\frac{dx}{\sqrt{1−x^2}}\)

23) \(\displaystyle ∫^3_0\frac{1}{x−1}\,dx\)

Answer

It diverges.

24) \(\displaystyle ∫^∞_1\frac{5}{x^3}\,dx\)

25) \(\displaystyle ∫^5_3\frac{5}{(x−4)^2}\,dx\)

Answer

It diverges.

 

In exercises 26 and 27, determine the convergence of each of the following integrals by comparison with the given integral. If the integral converges, find the number to which it converges.

26) \(\displaystyle ∫^∞_1\frac{dx}{x^2+4x};\) compare with \(\displaystyle ∫^∞_1\frac{dx}{x^2}\).

27) \(\displaystyle ∫^∞_1\frac{dx}{\sqrt{x}+1};\) compare with \(\displaystyle ∫^∞_1\frac{dx}{2\sqrt{x}}\).

Answer

Both integrals diverge.

 

In exercises 28 - 38, evaluate the integrals. If the integral diverges, answer “It diverges.”

28) \(\displaystyle ∫^∞_1\frac{dx}{x^e}\)

29) \(\displaystyle ∫^1_0\frac{dx}{x^π}\)

Answer

It diverges.

30) \(\displaystyle ∫^1_0\frac{dx}{\sqrt{1−x}}\)

31) \(\displaystyle ∫^1_0\frac{dx}{1−x}\)

Answer

It diverges.

32) \(\displaystyle ∫^0_{−∞}\frac{dx}{x^2+1}\)

33) \(\displaystyle ∫^1_{−1}\frac{dx}{\sqrt{1−x^2}}\)

Answer

Converges to \(π\).

34) \(\displaystyle ∫^1_0\frac{\ln x}{x}\,dx\)

35) \(\displaystyle ∫^e_0\ln(x)\,dx\)

Answer

Converges to \(0\).

36) \(\displaystyle ∫^∞_0xe^{−x}\,dx\)

37) \(\displaystyle ∫^∞_{−∞}\frac{x}{(x^2+1)^2}\,dx\)

Answer

Converges to \(0\).

38) \(\displaystyle ∫^∞_0e^{−x}\,dx\)

 

In exercises 39 - 44, evaluate the improper integrals. Each of these integrals has an infinite discontinuity either at an endpoint or at an interior point of the interval.

39) \(\displaystyle ∫^9_0\frac{dx}{\sqrt{9−x}}\)

Answer

Converges to \(6\).

40) \(\displaystyle ∫^1_{−27}\frac{dx}{x^{2/3}}\)

41) \(\displaystyle ∫^3_0\frac{dx}{\sqrt{9−x^2}}\)

Answer

Converges to \(\frac{π}{2}\).

42) \(\displaystyle ∫^{24}_6\frac{dt}{t\sqrt{t^2−36}}\)

43) \(\displaystyle ∫^4_0x\ln(4x)\,dx\)

Answer

Converges to \(8\ln(16)−4\).

44) \(\displaystyle ∫^3_0\frac{x}{\sqrt{9−x^2}}\,dx\)

 

45) Evaluate \(\displaystyle ∫^t_{.5}\frac{dx}{\sqrt{1−x^2}}.\) (Be careful!) (Express your answer using three decimal places.)

Answer

Converges to about \(1.047\).

46) Evaluate \(\displaystyle ∫^4_1\frac{dx}{\sqrt{x^2−1}}.\) (Express the answer in exact form.)

47) Evaluate \(\displaystyle ∫^∞_2\frac{dx}{(x^2−1)^{3/2}}.\)

Answer

Converges to \(−1+\frac{2}{\sqrt{3}}\).

48) Find the area of the region in the first quadrant between the curve \(y=e^{−6x}\) and the \(x\)-axis.

49) Find the area of the region bounded by the curve \(y=\dfrac{7}{x^2},\) the \(x\)-axis, and on the left by \(x=1.\)

Answer

\(A = 7.0\) units.²

50) Find the area under the curve \(y=\dfrac{1}{(x+1)^{3/2}},\) bounded on the left by \(x=3.\)

51) Find the area under \(y=\dfrac{5}{1+x^2}\) in the first quadrant.

Answer

\(A = \dfrac{5π}{2}\) units.²

52) Find the volume of the solid generated by revolving about the \(x\)-axis the region under the curve \(y=\dfrac{3}{x}\) from \(x=1\) to \(x=∞.\)

53) Find the volume of the solid generated by revolving about the \(y\)-axis the region under the curve \(y=6e^{−2x}\) in the first quadrant.

Answer

\(V = 3π\,\text{units}^3\)

54) Find the volume of the solid generated by revolving about the \(x\)-axis the area under the curve \(y=3e^{−x}\) in the first quadrant.

 

The Laplace transform of a continuous function over the interval \([0,∞)\) is defined by \(\displaystyle F(s)=∫^∞_0e^{−sx}f(x)\,dx\) (see the Student Project). This definition is used to solve some important initial-value problems in differential equations, as discussed later. The domain of \(F\) is the set of all real numbers s such that the improper integral converges. Find the Laplace transform \(F\) of each of the following functions and give the domain of \(F\).

55) \(f(x)=1\)

Answer

\(\dfrac{1}{s},\quad s>0\)

56) \(f(x)=x\)

57) \(f(x)=\cos(2x)\)

Answer

\(\dfrac{s}{s^2+4},\quad s>0\)

58) \(f(x)=e^{ax}\)

59) Use the formula for arc length to show that the circumference of the circle \(x^2+y^2=1\) is \(2π\).

Answer

Answers will vary.

 

A function is a probability density function if it satisfies the following definition: \(\displaystyle ∫^∞_{−∞}f(t)\,dt=1\). The probability that a random variable \(x\) lies between a and b is given by \(\displaystyle P(a≤x≤b)=∫^b_af(t)\,dt.\)

60) Show that \(\displaystyle f(x)=\begin{cases}0,&\text{if}\,x<0\\7e^{−7x},&\text{if}\,x≥0\end{cases}\) is a probability density function.

61) Find the probability that \(x\) is between \(0\) and \(0.3\). (Use the function defined in the preceding problem.) Use four-place decimal accuracy.

Answer

0.8775

Chapter Review Exercises

In exercises 1 - 4, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.

1) \(\displaystyle ∫e^x\sin(x)\,dx\) cannot be integrated by parts.

2) \(\displaystyle ∫\frac{1}{x^4+1}\,dx\) cannot be integrated using partial fractions.

Answer:

False

3) In numerical integration, increasing the number of points decreases the error.

4) Integration by parts can always yield the integral.

Answer:

False

 

In exercises 5 - 10, evaluate the integral using the specified method.

5) \(\displaystyle ∫x^2\sin(4x)\,dx,\) using integration by parts

6) \(\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx,\) using trigonometric substitution

Answer:

\(\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx = −\frac{\sqrt{x^2+16}}{16x}+C\)

7) \(\displaystyle ∫\sqrt{x}\ln x\,dx,\) using integration by parts

8) \(\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx,\) using partial fractions

Answer:

\(\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx = \frac{1}{10}\big(4\ln|2−x|+5\ln|x+1|−9\ln|x+3|\big)+C\)

9) \(\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}\,dx,\) using trigonometric substitution

10) \(\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx,\) using a table of integrals or a CAS

Answer:

\(\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx = −\frac{\sqrt{4−\sin^2(x)}}{\sin(x)}−\frac{x}{2}+C\)

 

In exercises 11 - 15, integrate using whatever method you choose.

11) \(\displaystyle ∫\sin^2 x\cos^2 x\,dx\)

12) \(\displaystyle ∫x^3\sqrt{x^2+2}\,dx\)

Answer:

\(\displaystyle ∫x^3\sqrt{x^2+2}\,dx = \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C\)

13) \(\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}\,dx\)

14) \(\displaystyle ∫\frac{1}{x^4+4}\,dx\)

Answer:

\(\displaystyle ∫\frac{1}{x^4+4}\,dx = \frac{1}{16}\ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}\tan^{−1}(1−x)+\frac{1}{8}\tan^{−1}(x+1)+C\)

15) \(\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}\,dx\)

 

In exercises 16 - 18, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.

16) [T] \(\displaystyle ∫^2_1\sqrt{x^5+2}\,dx\)

Answer:

\(M_4=3.312,\)
\(T_4=3.354,\)
\(S_4=3.326\)

17) [T] \(\displaystyle ∫^{\sqrt{π}}_0e^{−\sin(x^2)}\,dx\)

18) [T] \(\displaystyle ∫^4_1\frac{\ln(1/x)}{x}\,dx\)

Answer:

\(M_4=−0.982,\)
\(T_4=−0.917,\)
\(S_4=−0.952\)

 

In exercises 19 - 20, evaluate the integrals, if possible.

19) \(\displaystyle ∫^∞_1\frac{1}{x^n}\,dx,\) for what values of \(n\) does this integral converge or diverge?

20) \(\displaystyle ∫^∞_1\frac{e^{−x}}{x}\,dx\)

Answer:

approximately 0.2194

 

In exercises 21 - 22, consider the gamma function given by \(\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}\,dy.\)

21) Show that \(\displaystyle Γ(a)=(a−1)Γ(a−1).\)

22) Extend to show that \(\displaystyle Γ(a)=(a−1)!,\) assuming \(a\) is a positive integer.

 

The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.

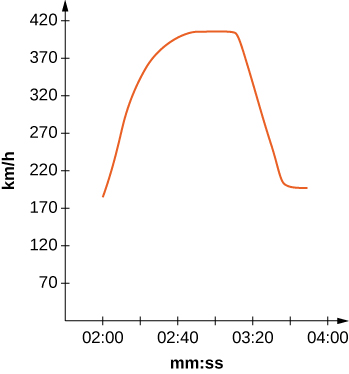
23) [T] Use the graph to estimate the velocity every 20 sec and fit to a graph of the form \(v(t)=ae^{bx}\sin(cx)+d.\) (Hint: Consider the time units.)

24) [T] Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.

Answer:

Answers may vary. Ex: \(9.405\) km

 

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.