3.2: First order linear equations

A first order differential equation is said to be \( \textcolor{blue}{\mbox{linear}} \) if it can be written as

\begin{equation}\label{eq:3.3.1}
y'+p(x)y=f(x),
\end{equation}

A first order differential equation that can't be written like this is \( \textcolor{blue}{\mbox{nonlinear}} \). We say that \eqref{eq:3.3.1} is \( \textcolor{blue}{\mbox{homogenous}} \) if \(f\equiv0\); otherwise it's \( \textcolor{blue}{\mbox{nonhomogeneous}} \).

Since \(y\equiv0\) is obviously a solution of the homogeneous equation \(y'+p(x)y=0\), we call it the \( \textcolor{blue}{\mbox{trivial solution}} \). Any other solution is \( \textcolor{blue}{\mbox{nontrivial}} \).

Example \(\PageIndex{1}\)

The first order equations

\begin{eqnarray*}
x^2y'+3y=x^2 \\
xy'-8x^2y=sin x \\
xy'+(\ln x)y=0 \\
y'=x^2y - 2 \\
\end{eqnarray*}

are not in the form \eqref{eq:3.3.1}, but they are linear, since they can be rewritten as

\begin{eqnarray*}
y'+{3\over x^2}y=1 \\
y'-8xy={\sin x\over x} \\
y'+{\ln x\over x}y=0 \\
y'-x^2y=-2 \\
\end{eqnarray*}

General Solution of a Linear First Order Equation

To motivate a definition that we'll need, consider the simple linear first order equation

\begin{equation}\label{eq:3.3.2}
y'={1\over x^2}.
\end{equation}

From calculus we know that \(y\) satisfies this equation if and only if

\begin{equation}\label{eq:3.3.3}
y=-\frac{1}{x}+c,
\end{equation}

where \(c\) is an arbitrary constant.

We call \(c\) a \( \textcolor{blue}{\mbox{parameter}} \) and say that \eqref{eq:3.3.2} defines a \( \textcolor{blue}{\mbox{one--parameter family}} \) of functions. For each real number \(c\), the function defined by \eqref{eq:3.3.3} is a solution of \eqref{eq:3.3.2} on \((-\infty,0)\) and \((0,\infty)\); moreover, every solution of \eqref{eq:3.3.2} on either of these intervals is of the form \eqref{eq:3.3.3} for some choice of \(c\). We say that \eqref{eq:3.3.3} is \( \textcolor{blue}{\mbox{the general solution}} \) of \eqref{eq:3.3.2}.

We'll see that a similar situation occurs in connection with any first order linear equation

\begin{equation}\label{eq:3.3.4}
y'+p(x)y=f(x);
\end{equation}

that is, if \(p\) and \(f\) are continuous on some open interval \((a,b)\) then there's a unique formula \(y=y(x,c)\) analogous to \eqref{eq:3.3.3} that involves \(x\) and a parameter \(c\) and has these properties:

For each fixed value of \(c\), the resulting function of \(x\) is a solution of \eqref{eq:3.3.4} on \((a,b)\). If \(y\) is a solution of \eqref{eq:3.3.4} on \((a,b)\), then \(y\) can be obtained from the formula by choosing \(c\) appropriately. We'll call \(y=y(x,c)\) the \( \textcolor{blue}{\mbox{general solution}} \) of \eqref{eq:3.3.4}. When this has been established, it will follow that an equation of the form

\begin{equation}\label{eq:3.3.5}
P_0(x)y'+P_1(x)y=F(x)
\end{equation}

has a general solution on any open interval \((a,b)\) on which \(P_0\), \(P_1\), and \(F\) are all continuous and \(P_0\) has no zeros, since in this case we can rewrite \eqref{eq:3.3.5} in the form \eqref{eq:3.3.4} with \(p=P_1/P_0\) and \(f=F/P_0\), which are both continuous on \((a,b)\).

To avoid awkward wording in examples and exercises, we won't specify the interval \((a,b)\) when we ask for the general solution of a specific linear first order equation. Let's agree that this always means that we want the general solution on every open interval on which \(p\) and \(f\) are continuous if the equation is of the form \eqref{eq:3.3.4}, or on which \(P_0\), \(P_1\), and \(F\) are continuous and \(P_0\) has no zeros, if the equation is of the form \eqref{eq:3.3.5}. We leave it to you to identify these intervals in specific examples and exercises.

For completeness, we point out that if \(P_0\), \(P_1\), and \(F\) are all continuous on an open interval \((a,b)\), but \(P_0\) \( \textcolor{blue}{\mbox{does}} \) have a zero in \((a,b)\), then \eqref{eq:3.3.5} may fail to have a general solution on \((a,b)\) in the sense just defined. Since this isn't a major point that needs to be developed in depth, we won't discuss it further.

Homogeneous Linear First Order Equations

We begin with the problem of finding the general solution of a homogeneous linear first order equation. The next example recalls a familiar result from calculus.

Example \(\PageIndex{2}\)

Let \(a\) be a constant.

a) Find the general solution of \begin{equation} y'-ay=0.\label{eq:3.3.6} \end{equation}

b) Solve the initial value problem \(y'-ay=0,\quad y(x_0)=y_0\)

Answer

a) You already know from calculus that if \(c\) is any constant, then \(y=ce^{ax}\) satisfies \eqref{eq:3.3.6}. However, let's pretend you've forgotten this, and use this problem to illustrate a general method for solving a homogeneous linear first order equation. We know that \eqref{eq:3.3.6} has the trivial solution \(\equiv0\). Now suppose \(y\) is a nontrivial solution of \eqref{eq:3.3.6}. Then, since a differentiable function must be continuous, there must be some open interval \(I\) on which \(y\) has no zeros.

We rewrite \eqref{eq:3.3.6} as \({y'\over y}=a\) for \(x\) in \(I\). Integrating this shows that \(\ln|y|=ax+k\), so \(|y|=e^ke^{ax}\) where \(k\) is an arbitrary constant. Since \(e^{ax}\) can never equal zero, \(y\) has no zeros, so \(y\) is either always positive or always negative. Therefore we can rewrite \(y\) as

\begin{equation}\label{eq:3.3.7} y=ce^{ax} \end{equation}

where \(c=\left\{\begin{array}{cl}\phantom{-}e^k&\mbox{if } y>0,\\ -e^k&\mbox{if } y<0.\end{array}\right.\)

This shows that every nontrivial solution of \eqref{eq:3.3.6} is of the form \(y=ce^{ax}\) for some nonzero constant \(c\). Since setting \(c=0\) yields the trivial solution, \({\color{blue}\it all}\) solutions of \eqref{eq:3.3.6} are of the form \eqref{eq:3.3.7}. Conversely, \eqref{eq:3.3.7} is a solution of \eqref{eq:3.3.6} for every choice of \(c\), since differentiating \eqref{eq:3.3.7} yields \(y'=ace^{ax}=ay\). Figure \(\PageIndex{1} \) shows the graphs of some solutions corresponding to various values of \(c\)

b) Imposing the initial condition \(y(x_0)=y_0\) yields \(y_0=ce^{ax_0}\), so \(c=y_0e^{-ax_0}\) and \(y=y_0e^{-ax_0}e^{ax}=y_0e^{a(x-x_0)}\)

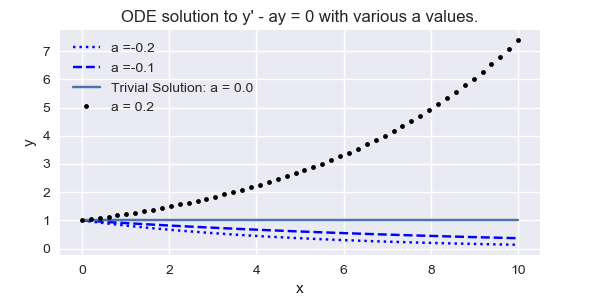
Figure \(\PageIndex{1}\): \(y' - ay = 0\) with various values of a

Example \(\PageIndex{3}\)

a) Find the general solution of \begin{equation} xy'+y=0.\label{eq:3.3.8} \end{equation}

b) Solve the initial value problem \begin{equation} xy'+y=0,\quad y(1)=3.\label{eq:3.3.9} \end{equation}

Answer

a) We rewrite \eqref{eq:3.3.8} as \begin{equation}\label{eq:3.3.10} y'+{1\over x}y=0, \end{equation} where \(x\) is restricted to either \((-\infty,0)\) or \((0,\infty)\). If

\(y\) is a nontrivial solution of \eqref{eq:3.3.10}, there must be some open interval \(I\) on which \(y\) has no zeros. We can rewrite \eqref{eq:3.3.10} as \({y'\over y}=-{1\over x}\) for \(x\) in \(I\). Integrating shows that \(\ln|y|=-\ln|x|+k\) so \(|y|={e^k\over|x|}\).

Since a function that satisfies the last equation can't change sign on either \((-\infty,0)\) or \((0,\infty)\), we can rewrite this result more simply as \begin{equation}\label{eq:3.3.11} y={c\over x} \end{equation}

where \(c=\left\{\begin{array}{cl}\phantom{-}e^k&\mbox{if } y>0,\\ -e^k&\mbox{if } y<0.\end{array}\right.\)

We've now shown that every solution of \eqref{eq:3.3.10} is given by \eqref{eq:3.3.11} for some choice of \(c\). (Even though we assumed that \(y\) was nontrivial to derive \eqref{eq:3.3.11}, we can get the trivial solution by setting \(c=0\) in \eqref{eq:3.3.11}.) Conversely, any function of the form \eqref{eq:3.3.11} is a solution of \eqref{eq:3.3.10}, since differentiating \eqref{eq:3.3.11} yields \(y'=-{c\over x^2}\), and substituting this and \eqref{eq:3.3.11} into \eqref{eq:3.3.10} yields

\begin{eqnarray*}
y'+{1\over x}y=-{\frac{c} {x^2}}+{\frac{1}{x}}{\frac{c}{x}}\\=-{\frac{c}{x^2}}+{\frac{c}{x^2}}=0.
\end{eqnarray*}

Figure \(\PageIndex{2} \) shows the graphs of some solutions corresponding to various values of \(c\)

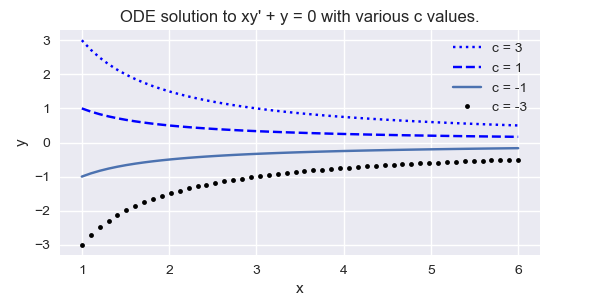
Figure \(\PageIndex{2}\): \(xy' + y = 0\) with various values of c

b) Imposing the initial condition \(y(1)=3\) in \eqref{eq:3.3.11} yields \(c=3\). Therefore the solution of \eqref{eq:3.3.9} is \(y={3\over x}\).

The interval of validity of this solution is \((0,\infty)\).

The results in Example 3 are special cases of the next theorem.

Theorem \(\PageIndex{1}\)

If \(p\) is continuous on \((a,b),\) then the general solution of the homogeneous equation \begin{equation}\label{eq:3.3.12} y'+p(x)y=0 \end{equation} on \((a,b)\) is \(y=ce^{-P(x)}\),

where \begin{equation}\label{eq:3.3.13} P(x)=\int p(x)\,dx \end{equation} is any antiderivative of \(p\) on \((a,b);\) that is,

\begin{equation}\label{eq:3.3.14} P'(x)=p(x),\quad a<x<b. \end{equation}

Proof

If \(y=ce^{-P(x)}\), differentiating \(y\) and using \eqref{eq:3.3.14} shows that \(y'=-P'(x)ce^{-P(x)}=-p(x)ce^{-P(x)}=-p(x)y,\) so \(y'+p(x)y=0\); that is, \(y\) is a solution of \eqref{eq:3.3.12}, for any choice of \(c\).

Now we'll show that any solution of \eqref{eq:3.3.12} can be written as \(y=ce^{-P(x)}\) for some constant \(c\). The trivial solution can be written this way, with \(c=0\). Now suppose \(y\) is a nontrivial solution. Then there's an open subinterval \(I\) of \((a,b)\) on which \(y\) has no zeros. We can rewrite \eqref{eq:3.3.12} as \begin{equation}\label{eq:3.3.15} {y'\over y}=-p(x) \end{equation} for \(x\) in \(I\). Integrating \eqref{eq:3.3.15} and recalling \eqref{eq:3.3.13} yields \(\ln|y|=-P(x) + k,\) where \(k\) is a constant. This implies that \(|y|=e^ke^{-P(x)}.\)

Since \(P\) is defined for all \(x\) in \((a,b)\) and an exponential can never equal zero, we can take \(I=(a,b)\), so \(y\) has zeros on \((a,b)\) so we can rewrite the last equation as \(y=ce^{-P(x)}\),

where \(c=\left\{\begin{array}{cl}\phantom{-}e^k&\mbox{if } y>0\mbox{ on } (a,b),\\ -e^k&\mbox{if } y<0\mbox{ on }(a,b).\end{array}\right.\)

Rewriting a first order differential equation so that one side depends only on \(y\) and \(y'\) and the other depends only on \(x\) is called \( \textcolor{blue}{\mbox{separation of variables}} \). In rewriting \eqref{eq:3.3.12} as \eqref{eq:3.3.15}. We'll apply this method to nonlinear equations in Section 3.2.

Linear Nonhomogeneous First Order Equations

We'll now solve the nonhomogeneous equation \begin{equation}\label{eq:3.3.16} y'+p(x)y=f(x). \end{equation}

When considering this equation we call \(y'+p(x)y=0\) the \( \textcolor{blue}{\mbox{complementary equation}} \).

We'll find solutions of \eqref{eq:3.3.16} in the form \(y=uy_1\), where \(y_1\) is a nontrivial solution of the complementary equation and \(u\) is to be determined. This method of using a solution of the complementary equation to obtain solutions of a nonhomogeneous equation is a special case of a method called \( \textcolor{blue}{\mbox{variation of parameters}} \), which you'll encounter several times in this book.

(Obviously, \(u\) can't be constant, since if it were, the left side of \eqref{eq:3.3.16} would be zero. Recognizing this, the early users of this method viewed \(u\) as a ``parameter'' that varies; hence, the name "variation of parameters.'')

If \(y=uy_1\) then \( y'=u'y_1+uy_1'\). Substituting these expressions for \(y\) and \(y'\) into \eqref{eq:3.3.16} yields \(u'y_1+u(y_1'+p(x)y_1)=f(x),\) which reduces to \begin{equation}\label{eq:3.3.17} u'y_1=f(x) \end{equation}

since \(y_1\) is a solution of the complementary equation; that is, \(y_1'+p(x)y_1=0.\)

In the proof of Theorem 3.2.1 we saw that \(y_1\) has no zeros on an interval where \(p\) is continuous. Therefore we can divide \eqref{eq:3.3.17} through by \(y_1\) to obtain \(u'=f(x)/y_1(x).\) We can integrate this (introducing a constant of integration), and multiply the result by \(y_1\) to get the general solution of \eqref{eq:3.3.16}. Before turning to the formal proof of this claim, let's consider some examples.

Example \(\PageIndex{4}\):

Find the general solution of \begin{equation}\label{eq:3.3.18} y'+2y=x^3e^{-2x}.\end{equation}

Answer

By applying part(a) of Example 3.2.3 with \(a=-2\), we see that \(y_1=e^{-2x}\) is a solution of the complementary equation \(y'+2y=0\). Therefore we seek solutions of \eqref{eq:3.3.18} in the form \(y=ue^{-2x}\), so that \begin{equation} \label{eq:3.3.19} y'=u'e^{-2x}-2ue^{-2x} \text{ and } y'+2y=u'e^{-2x}-2ue^{-2x}+2ue^{-2x}=u'e^{-2x} \end{equation}

Therefore \(y\) is a solution of \eqref{eq:3.3.18} if and only if \(u'e^{-2x}=x^3e^{-2x}\) or, equivalently, \(u'=x^3.\)

Therefore \(u={x^4\over4}+c \) and \(y=ue^{-2x}=e^{-2x}\left({x^4\over4}+c\right)\) is the general solution of \eqref{eq:3.3.18}.

Figure \(\PageIndex{3} \) shows some integral curves for \eqref{eq:3.3.18}.

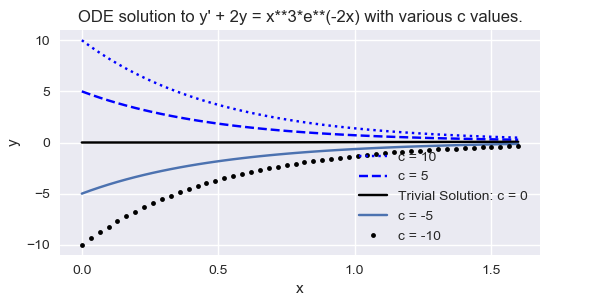
Figure \(\PageIndex{3}\): Some solutions to \(y' +2y =x^3e^{-2x}\)

Example \(\PageIndex{5}\):

(a) Find the general solution \begin{equation}\label{eq:3.3.20} y'+(\cot x)y=x\csc x.\end{equation}

(b) Solve the initial value problem \begin{equation}\label{eq:3.3.21} y'+(\cot x)y=x\csc x,\quad y(\pi/2)=1.\end{equation}

Answer

(a) Here \(p(x)=\cot x\) and \(f(x)= x\csc x\) are both continuous except at the points \(x=r\pi\), where \(r\) is an integer.Therefore we seek solutions of \eqref{eq:3.3.20} on the intervals \(\left(r\pi, (r+1)\pi \right)\). We need a nontrival solution \(y_1\) of the complementary equation; thus, \(y_1\) must satisfy \(y_1'+(\cot x)y_1=0\), which we rewrite as \begin{equation}\label{eq:3.3.22} {y_1'\over y_1}=-\cot x=-{\cos x\over\sin x} \end{equation}

Integrating this yields \(\ln|y_1|=-\ln|\sin x|,\) where we take the constant of integration to be zero since we need only \( \textcolor{blue}{\mbox{one}} \) function that satisfies \eqref{eq:3.3.22}. Clearly \(y_1=1/\sin x\) is a suitable choice. Therefore we seek solutions of \eqref{eq:3.3.20} in the form \(y={u\over\sin x},\) so that \begin{equation} \label{eq:3.3.23} y'={u'\over\sin x}-{u\cos x\over\sin^2x} \end{equation}

and \begin{equation}\label{eq:3.3.24} y'+(\cot x)y={u' \over \sin x}-{u \cos x \over \sin^2x}+{u \cot x \over \sin x}={u' \over \sin x}-{u \cos x \over\sin^2x}+{u\cos x\over\sin^2 x}={u'\over\sin x}.\end{equation}

Therefore \(y\) is a solution of \eqref{eq:3.3.20} if and only if \(\frac{u'}{\sin x}=x\csc x=\frac{x}{\sin x}\) or, equivalently, \( u'=x.\)

Integrating this yields

\begin{equation}\label{eq:3.3.25} u={x^2\over2}+c, \text y={u\over\sin x}= {x^2\over 2\sin x}+ {c\over\sin x}. \end{equation}

is the general solution of \eqref{eq:3.3.20} on every interval \(\left(r\pi,(r+1)\pi\right)\) (\(r=integer)\).

(b) Imposing the initial condition \(y(\pi/2)=1\) in \eqref{eq:3.3.25} yields \(1=\frac{\pi^2}{8}+c\) or \(c=1-\frac{\pi^2}{8}.\)

Thus,\(y={x^2\over 2\sin x}+{(1-\pi^2/8)\over\sin x}\) is a solution of \eqref{eq:3.3.21}. The interval of validity of this solution is \((0,\pi)\);

Figure \(\PageIndex{4} \) shows its graph.

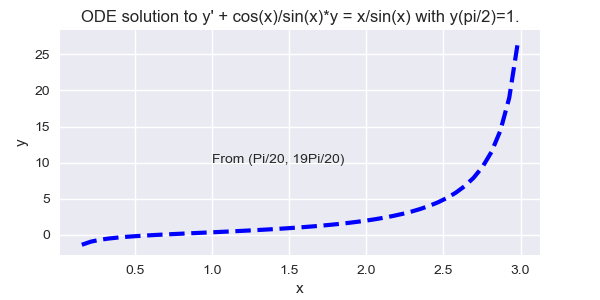
Figure \(\PageIndex{4}\): \(y'+\cot(x)y = x\csc(x)\)

It wasn't necessary to do the computations \eqref{eq:3.3.23} and \eqref{eq:3.3.24} in Example \(\PageIndex{5}\) since we showed in the discussion preceding Example \(\PageIndex{5}\) that if \(y=uy_1\) where \(y_1'+p(x)y_1=0\), then \(y'+p(x)y=u'y_1\). We did these computations so you would see this happen in this specific example. We recommend that you include these "unnecesary'' computations in doing exercises, until you're confident that you really understand the method. After that, omit them.

We summarize the method of variation of parameters for solving \begin{equation} \label{eq:3.3.26} y'+p(x)y=f(x) \end{equation} as follows:

(a) Find a function \(y_1\) such that \({y_1'\over y_1}=-p(x).\)

For convenience, take the constant of integration to be zero.

(b) Write \begin{equation} \label{eq:3.3.27} y=uy_1 \end{equation} to remind yourself of what you're doing.

(c) Write \(u'y_1=f\) and solve for \(u'\); thus, \(u'=f/y_1\).

(d) Integrate \(u'\) to obtain \(u\), with an arbitrary constant of integration.

(e) Substitute \(u\) into \eqref{eq:3.3.27} to obtain \(y\).

To solve an equation written as \(P_0(x)y'+P_1(x)y=F(x)\) we recommend that you divide through by \(P_0(x)\) to obtain an equation of the form \eqref{eq:3.3.26} and then follow this procedure.

Solutions in Integral Form

Sometimes the integrals that arise in solving a linear first order equation can't be evaluated in terms of elementary functions. In this case the solution must be left in terms of an integral.

Example \(\PageIndex{6}\):

(a) Find the general solution of \(y'-2xy=1.\)

(b) Solve the initial value problem \begin{equation}\label{eq:3.3.28} y'-2xy=1, y(0)=y_0. \end{equation}

Answer

(a) To apply variation of parameters, we need a nontrivial solution \(y_1\) of the complementary equation; thus, \(y_1'-2xy_1=0\), which we rewrite as \({y_1'\over y_1}=2x.\)

Integrating this and taking the constant of integration to be zero yields \(\ln|y_1|=x^2, |y_1|=e^{x^2}.\)

We choose \(y_1=e^{x^2}\) and seek solutions of \eqref{eq:3.3.28} in the form \(y=ue^{x^2}\), where \(u'e^{x^2}=1, u'=e^{-x^2}\).

Therefore \(u=c+\int e^{-x^2}dx,\) but we can't simplify the integral on the right because there's no elementary function with derivative equal to \(e^{-x^2}\)

Therefore the best available form for the general solution of \eqref{eq:3.3.28} is \begin{equation}\label{eq:3.3.29} y=ue^{x^2}= e^{x^2}\left(c+\int e^{-x^2}dx\right). \end{equation}

(b) Since the initial condition in \eqref{eq:3.3.28} is imposed at \(x_0=0\), it is convenient to rewrite \eqref{eq:3.3.29} as \(y=e^{x^2}\left(c+\int^x_0 e^{-t^2} dt\right), \int_0^0e^{-t^2}\,dt=0.\)

Setting \(x=0\) and \(y=y_0\) here shows that \(c=y_0\). Therefore the solution of the initial value problem is \begin{equation}\label{eq:3.3.30} y=e^{x^2}\left(y_0 +\int^x_0 e^{-t^2}dt\right).\end{equation}

For a given value of \(y_0\) and each fixed \(x\), the integral on the right can be evaluated by numerical methods. An alternate procedure is to apply the numerical integration procedures discussed in Chapter 3 directly to the initial value problem \eqref{eq:3.3.28}.

Figure~\ref{figure:2.1.5} shows graphs of \eqref{eq:3.3.30} for several values of \(y_0\).

\begin{figure}[H]

\centering

\scalebox{.9}{

\includegraphics[bb=-78 148 689 643,width=5.67in,height=3.66in,keepaspectratio]{fig020105} }

\color{blue}

\caption{Solutions of $y'-2xy=1$, $y(0)=y_{0}$}

\label{figure:2.1.5}

\end{figure}

An Existence and Uniqueness Theorem

The method of variation of parameters leads to this theorem.

Theorem \(\PageIndex{2}\)

Suppose \(p\) and \(f\) are continuous on an open interval \((a,b),\) and let \(y_1\) be any nontrivial solution of the complementary equation \(y'+p(x)y=0\) on \((a,b)\).

Then:

(a) The general solution of the nonhomogeneous equation \begin{equation}\label{eq:3.3.31} y'+p(x)y=f(x) \end{equation} on \((a,b)\) is

\begin{equation}\label{eq:3.3.32} y=y_1(x)\left(c +\int f(x)/y_1(x)\,dx\right) \end{equation}

(b) If \(x_0\) is an arbitrary point in \((a,b)\) and \(y_0\) is an arbitrary real number, then the initial value problem \(y'+p(x)y=f(x),\quad y(x_0)=y_0\) has the unique solution

\(y=y_1(x)\left({y_0\over y_1(x_0)} +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right)\) on \((a,b)\)

Proof

(a) To show that \eqref{eq:3.3.32} is the general solution of \eqref{eq:3.3.31} on \((a,b)\), we must prove that:

(i) If \(c\) is any constant, the function \(y\) in \eqref{eq:3.3.32} is a solution of \eqref{eq:3.3.31} on \((a,b)\).

(ii) If \(y\) is a solution of \eqref{eq:3.3.31} on \((a,b)\) then \(y\) is of the form \eqref{eq:3.3.32} for some constant \(c\).

To prove \part{i}, we first observe that any function of the form \eqref{eq:3.3.32} is defined on \((a,b)\), since \(p\) and \(f\) are continuous on \((a,b)\). Differentiating \eqref{eq:3.3.32} yields \(y'=y_1'(x)\left(c +\int f(x)/y_1(x)\,dx\right)+f(x).\)

Since \(y_1'=-p(x)y_1\), this and \eqref{eq:3.3.32} imply that \begin{eqnarray*} y'&=&-p(x)y_1(x)\left(c +\int f(x)/y_1(x)\, dx\right)+f(x)\\&=&-p(x)y(x)+f(x),\end{eqnarray*}

which implies that \(y\) is a solution of \eqref{eq:3.3.31}.

To prove \part{ii}, suppose \(y\) is a solution of \eqref{eq:3.3.31} on \((a,b)\). From the proof of Theorem~\ref{thmtype:3.3.1}, we know that \(y_1\) has no zeros on \((a,b)\), so the function \(u=y/y_1\) is defined on \((a,b)\).

Moreover, since \(y'=-py+f y_1'=-py_1,\)

\begin {eqnarray*}u'&=&{y_1y'-y_1'y\over y_1^2}\\&=&{y_1(-py+f)-(-py_1)y\over y_1^2}={f\over y_1}\end{eqnarray*}

Integrating \(u'=f/y_1\) yields \(u=\left(c +\int f(x)/y_1(x)\, dx\right),\) which implies \eqref{eq:3.3.32}, since \(y=uy_1\).

(b) We've proved \part{a}, where \(\int f(x)/y_1(x)\,dx\) in \eqref{eq:3.3.32} is an arbitrary antiderivative of \(f/y_1\). Now it's convenient to choose the antiderivative that equals zero when \(x=x_0\), and write the general solution of \eqref{eq:3.3.31} as \(y=y_1(x)\left(c +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right).\)

Since \(y(x_0)= y_1(x_0)\left(c +\int^{x_0}_{x_0} {f(t)\over y_1(t)}\, dt\right)=cy_1(x_0),\) we see that \(y(x_0)=y_0\) if and only if \(c=y_0/y_1(x_0)\).