2.4: Solve Systems of Linear Equations with Three Variables
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Determine whether an ordered triple is a solution of a system of three linear equations with three variables
- Solve a system of linear equations with three variables
- Solve applications using systems of linear equations with three variables
Before you get started, take this readiness quiz.
- Evaluate 5x−2y+3z when x=−2,y=−4, and z=3.
- Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. {−2x+y=−11x+3y=9
- Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. {7x+8y=43x−5y=27
Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables
In this section, we will extend our work of solving a system of linear equations. So far we have worked with systems of equations with two equations and two variables. Now we will work with systems of three equations with three variables. But first let's review what we already know about solving equations and systems involving up to two variables.
We learned earlier that the graph of a linear equation, Ax+By=C, is a line. Each point on the line is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions
We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.
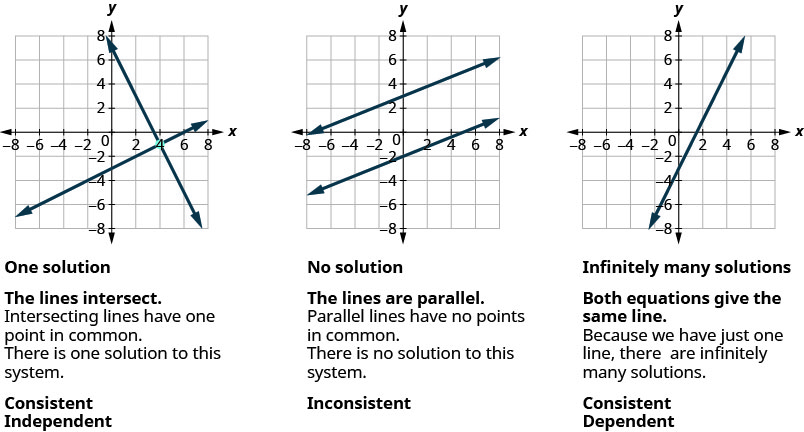
Similarly, for a linear equation with three variables Ax+By+Cz=D every solution to the equation is an ordered triple, (p,q,r) that makes the equation true when substituted in for (x,y,z.
1. An expression that can be written as
Ax+By+Cz
with A, B, and C real numbers, not all zero, is called a linear expression (with three variables), or more specifically, a linear expression with x, y, and z.
2. An equation that can be written as
Ax+By+Cz=D
with A, B, C, and D real numbers, not all zero, is called a linear equation (with three variables), or more specifically, a linear equation with x, y, and z.
As before, triples of numbers can be graphed in three dimensional space, so we will call these triples points and imagine them in this space. All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.
When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

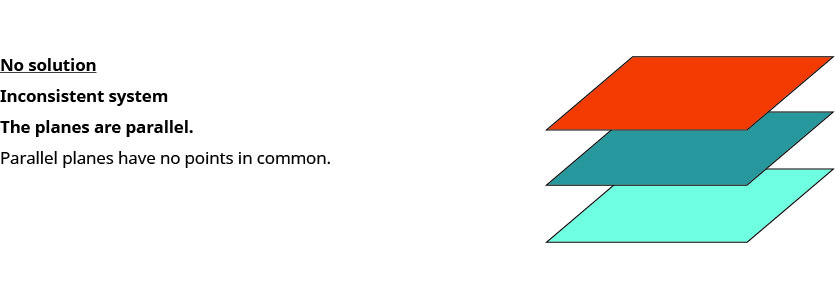






To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple (x,y,z) that makes all three equations true. These are called the solutions of the system of three linear equations with three variables.
Solutions of a system of equations are the values of the variables that, when substituted, make all the equations true. A solution of a system of linear equations with three variables is represented by an ordered triple (p,q,r), so that substituting p for x, q for y. and r for z yields three true equations. We may also say (x,y,z)=(p,q,r) is a solution.
To determine if an ordered triple is a solution to a system of three equations, we substitute the values of the variables into each equation. If the ordered triple makes all three equations true, it is a solution to the system.
Determine whether the ordered triple is a solution to the system {x−y+z=22x−y−z=−62x+2y+z=−3.
a. (−2,−1,3)
b. (−4,−3,4)
- Solution
-
a.
{x−y+z=22x−y−z=−62x+2y+z=−3 We substitute x=−2, y=−1 and z=3 into all three equations. x−y+z=2−2−(−1)+3?=22?=2True 2x−y−z=−62(−2)−(−1)−3?=−6−6?=−6True 2x+2y+z=−32(−2)+2(−1)+3?=−3−3?=−3True Answer: (−2,−1,3) does make all three equations true, so (−2,−1,3) is a solution. b.
{x−y+z=22x−y−z=−62x+2y+z=−3 We substitute x=−4, y=−3 and z=4 into all three equations. x−y+z=2−4−(−3)+4?=23?=2False 2x−y−z=−62(−4)−(−3)−4?=−6−9?=−6False 2x+2y+z=−32(−4)+2(−3)+4?=−3−10?=−3False Answer: (−4,−3,4) does not make all three equations true, so (−4,−3,4) is not a solution.
Determine whether the ordered triple is a solution to the system {3x+y+z=2x+2y+z=−33x+y+2z=4.
a. (1,−3,2)
b. (4,−1,−5)
- Answer
-
a. Yes, it is a solution.
b. No, it is not a solution.
Determine whether the ordered triple is a solution to the system {x−3y+z=−5−3x−y−z=12x−2y+3z=1.
a. (2,−2,3)
b. (−2,2,3)
- Answer
-
a. No, it is not a solution.
b. Yes, it is a solution.
Solve a System of Linear Equations with Three Variables
To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable. This will then give us a system of equations with only two variables and then we know how to solve that system!
Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.
Solve the system {x−2y+z=32x+y+z=43x+4y+3z=−1 by elimination.
- Solution
-
{x−2y+z=32x+y+z=43x+4y+3z=−1 Write the equations in standard form.
- If any coefficients are fractions, clear them.
The equations are in standard form.
There are no fractions.
{x−2y+z=3(A)2x+y+z=4(B)3x+4y+3z=−1(C) Eliminate the same variable from two equations.
- Decide which variable you will eliminate.
- Work with a pair of equations to eliminate the chosen variable.
- Multiply one of both equations so that the coefficients of that variable are opposites.
- Add the equations to eliminate one variable.
We can eliminate the y's from Equations A and B by multiplying Equation B by 2.
Multiply.
We add the x's, y's, and constants. The new equation, D, has only x and z.
Add.
{x−2y+z=3(A)2x+y+z=4(B)
{x−2y+z=3(A)2(2x+y+z)=2(4)(B)
{x−2y+z=3(A)4x+2y+2z=8(B)
5x+3z=11(D)
Repeat the previous step using two other equations and eliminate the same variable as in the previous step. We can again eliminate the y's using the Equations (A) and (C) by multiplying Equation (A) by 2.
Add the new equations and the result will be Equation (E).
{x−2y+z=3(A)3x+4y+3z=−1(C)
{2(x−2y+z)=2(3)(A)3x+4y+3z=−1(C)
{2x−4y+2z=6(A)3x+4y+3z=−1(C)
5x+5z=5(E)
The two new equations form a system of two equations with two variables. Solve this system. Use Equations (D) and (E) to eliminate either x or z.
Add and solve for z.
Use either Equations (D) or (E) to solve for x using substitution.
{5x+3z=11(D)5x+5z=5(E)
{5x+3z=11(D)(−1)(5x+5z)=(−1)(5)(E)
{5x+3z=11(D)−5x−5z=−5(E)
−2z=6z=−3
5x+3z=11(D)5x+3(−3)=115x−9=115x=20x=4
Use the values of the two variables found in the previous step to solve for the third variable. Use an original equation to find y. 2x+y+z=4(B)2(4)+y+z=48+y−3=4y=−1 Write the solution as an ordered triple. Write it as (x,y,z). (4,−1,−3) Check that the ordered triple is a solution to all three original equations. This step will help to detect errors. Substitute x=4, y=−1 and z=−3 into all three equations.
Do they make the equations true?
x−2y+z=34−2(−1)+(−3)?=33?=3True
2x+y+z=42(4)+(−1)+(−3)?=44?=4True
3x+4y+3z=−13(4)+4(−1)+3(−3)?=−1−1?=−1True
Substituting 4 into x, −1 into y, and −3 into for z makes both equations true.
Answer the question. The solution is (4,−1,−3).
Solve the system {3x+y−z=22x−3y−2z=14x−y−3z=0 by elimination.
- Answer
-
The solution is (2,−1,3).
Solve the system {4x+y+z=−1−2x−2y+z=22x+3y−z=1 by elimination.
- Answer
-
The solution is (−2,3,4).
The steps are summarized here.
- Write the equations in standard form.
- If any coefficients are fractions, clear them.
- Eliminate the same variable from two equations.
- Decide which variable you will eliminate.
- Work with a pair of equations to eliminate the chosen variable.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Add the equations resulting from Step 2 to eliminate one variable.
- Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
- The two new equations form a system of two equations with two variables. Solve this system.
- Use the values of the two variables found in Step 4 to solve for the third variable.
- Write the solution as an ordered triple.
- Check that the ordered triple is a solution to all three original equations (in order to detect errors).
Solve the system {3x−4z=03y+2z=−32x+3y=−5.
- Solution
-
{3x−4z=0(A)3y+2z=−3(B)2x+3y=−5(C)
We can eliminate z from Equations (A) and (B) by multiplying Equation (B) by 2 and then adding the resulting equations.
{3x−4z=0(A)2(3y+2z)=2(−3)(B)
{3x−4z=0(A)6y+4z=−6(B)
Add. 3x+6y=−6(D) Notice that Equations (C) and (D) both have the variables x and y. We will solve this new system for x and y.
{2x+3y=−5(C)3x+6y=−6(D)
{(−2)(2x+3y)=(−2)(−5)(C)3x+6y=−6(D)
{−4x−6y=10(C)3x+6y=−6(D)
Add and solve for x. −x=4x=−4 To solve for y, we substitute x=−4 into Equation (C). 2x+3y=−5(C)2(−4)+3y=−5−8+3y=−53y=3y=1 We now have x=−4 and y=1. We need to solve for z. We can substitute x=−4 into Equation (A) to find z. 3x−4z=0(A)3(−4)−4z=0−12−4z=0−4z=12z=−3 We write the solution as an ordered triple. (−4,1,−3) We check that the solution makes all three equations true. 3x−4z=0(A)3(−4)−4(−3)?=00?=0True
3y+2z=−3(B)3(1)+2(−3)?=−3−3?=−3True
2x+3y=−5(C)2(−4)+3(1)?=−5−5?=−5True
(−4,1,−3) makes all three equations true.
Answer the question. The solution is (−4,1,−3).
Solve the system {3x−4z=−12y+3z=22x+3y=6.
- Answer
-
The solution is (−3,4,−2).
Solve the system {4x−3z=−53y+2z=73x+4y=6.
- Answer
-
The solution is (−2,3,−1).
When we solve a system and end up with no variables and a false statement, we know there are no solutions and that the system is inconsistent. The next example shows a system of equations that is inconsistent.
Solve the system {x+2y−3z=−1x−3y+z=12x−y−2z=2.
- Solution
-
{x+2y−3z=−1(A)x−3y+z=1(B)2x−y−2z=2(C) Use Equations (A) and (B) to eliminate z. {x+2y−3z=−1(A)x−3y+z=1(B)
{x+2y−3z=−1(A)(3)(x−3y+z)=(3)(1)(B)
{x+2y−3z=−1(A)3x−9y+3z=3(B)
Add. 4x−7y=2(D) Use Equations (B) and (C) to eliminate z again. {x−3y+z=1(B)2x−y−2z=2(C)
{(2)(x−3y+z)=(2)(1)(B)2x−y−2z=2(C)
{2x−6y+2z=2(B)2x−y−2z=2(C)
Add. 4x−7y=4(E) Use Equations (D) and (E) to eliminate a variable. {4x−7y=2(D)4x−7y=4(E)
{4x−7y=2(D)(−1)(4x−7y)=(−1)(4)(E)
{4x−7y=2(D)−4x+7y=−4(E)
Add. 0=−2 False Answer the question. We are left with a false statement and this tells us the system is inconsistent and has no solution.
Solve the system {x+2y+6z=5−x+y−2z=3x−4y−2z=1.
- Answer
-
The system has no solution.
Solve the system {2x−2y+3z=64x−3y+2z=0−2x+3y−7z=1.
- Answer
-
The system has no solution.
When we solve a system and end up with no variables but a true statement, we know there are infinitely many solutions. The system is consistent with dependent equations. Our solution will show how two of the variables depend on the third.
Solve the system {x+2y−z=12x+7y+4z=11x+3y+z=4.
- Solution
-
{x+2y−z=1(A)2x+7y+4z=11(B)x+3y+z=4(C) Use Equations (A) and (C) to eliminate x. {x+2y−z=1(A)x+3y+z=4(C)
{(−1)(x+2y−z)=(−1)(1)(A)2x+7y+4z=11(B)x+3y+z=4(C)
{−x−2y+z=−1(A)2x+7y+4z=11(B)x+3y+z=4(C)
Add. y+2z=3(D) Use Equations (A) and (B) to eliminate x again. {x+2y−z=1(A)2x+7y+4z=11(B)
{(−2)(x+2y−z)=(−2)(1)(A)2x+7y+4z=11(B)
{−2x−4y+2z=−2(A)2x+7y+4z=11(B)
Add. 3y+6z=9(E) Use Equations (D) and (E) to eliminate y. {y+2z=3(D)3y+6z=9(E)
{(−3)(y+2z)=(−3)(3)(D)3y+6z=9(E)
{−3y−6z=−9(D)3y+6z=9(E)
Add. 0=0 Conclusion. There are infinitely many solutions. Represent the solution showing how x and y are dependent on z.
Solve Equation (D) for y.
y+2z=3(D)y=−2z+3
Substitute y=−2z+3 into Equation (A) and solve for x. x+2y−z=1(A)x+2(−2z+3)−z=1x−4z+6−z=1x−5z+6=1x=5z−5
Answer the question. The true statement 0=0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form (x,y,z) where x=5z−5, y=−2z+3, and z is any real number.
Solve the system {x+y−z=02x+4y−2z=63x+6y−3z=9.
- Answer
-
The system has infinitely many solutions (x,3,z) where x=z−3 and z is any real number.
Solve the system {x−y−z=1−x+2y−3z=−43x−2y−7z=0.
- Answer
-
The system has infinitely many solutions (x,y,z) where x=5z−2, y=4z−3, and z is any real number.
Solve Applications using Systems of Linear Equations with Three Variables
Applications that are modeled by a system of equations can be solved using the same techniques we used to solve the systems. Many of the application are just extensions to three variables of the types we have solved earlier.
The community college theater department sold three kinds of tickets to its latest play production. The adult tickets sold for $15, the student tickets for $10, and the child tickets for $8. The theater department was thrilled to have sold 250 tickets and brought in $2,825 in one night. The number of student tickets sold is twice the number of adult tickets sold. How many of each type did the department sell?
- Solution
-
We will use a chart to organize the information. 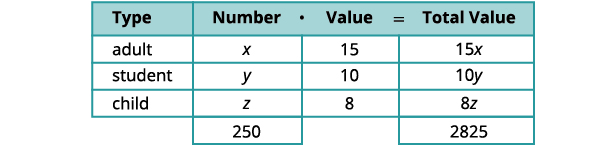
Number of students is twice number of adults. y=2x Rewrite the equation in standard form. y=2x2x−y=0 Write the system of equations. {x+y+z=250(A)15x+10y+8z=2825(B)−2x+y=0(C) Use Equations (A) and (B) to eliminate z. {x+y+z=250(A)15x+10y+8z=2825(B)
{(−8)(x+y+z)=(−8)(250)(A)15x+10y+8z=2825(B)
{−8x−8y−8z=−2000(A)15x+10y+8z=2825(B)
Add. 7x+2y=825(D) Use Equations (C) and (D) to eliminate y. {−2x+y=0(C)7x+2y=825(D)
{(−2)(−2x+y)=(−2)(0)(C)7x+2y=825(D)
{4x−2y=0(C)7x+2y=825(D)
Add and solve for x 11x=825x=75 adult tickets Use Equation (C) to find y. −2x+y=0(C) Substitute x=75. −2(75)+y=0−150+y=0y=150 student tickets Use Equation (A) to find z. x+y+z=250 Substitute in the values x=75 and y=150.
75+150+z=250225+z=250z=25 child ticketsAnswer the question. The theater department sold 75 adult tickets, 150 student tickets, and 25 child tickets.
Note that there are many ways of solving this but they all lead to the same solution.
The community college fine arts department sold three kinds of tickets to its latest dance presentation. The adult tickets sold for $20, the student tickets for $12 and the child tickets for $10. The fine arts department was thrilled to have sold 350 tickets and brought in $4,650 in one night. The number of child tickets sold is the same as the number of adult tickets sold. How many of each type did the department sell?
- Answer
-
The fine arts department sold 75 adult tickets, 200 student tickets, and 75 child tickets.
The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?
- Answer
-
The soccer team sold 200 adult tickets, 300 student tickets, and 100 child tickets.
Key Concepts
- Linear Equation in Three Variables: A linear equation with three variables, where A, B, C, and D are real numbers and A, B, and C are not all 0, is of the form
Ax+By+Cz=D
Every solution to the equation is an ordered triple, (p,q,r) that makes the equations true when p,q, and r are substituted in for x,y, and z, respectively. - How to solve a system of linear equations with three variables.
- Write the equations in standard form
If any coefficients are fractions, clear them. - Eliminate the same variable from two equations.
Decide which variable you will eliminate.
Work with a pair of equations to eliminate the chosen variable.
Multiply one or both equations so that the coefficients of that variable are opposites.
Add the equations resulting from Step 2 to eliminate one variable - Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
- The two new equations form a system of two equations with two variables. Solve this system.
- Use the values of the two variables found in Step 4 to find the third variable.
- Write the solution as an ordered triple.
- Check that the ordered triple is a solution to all three original equations.
- Write the equations in standard form
Glossary
- solutions of a system of linear equations with three variables
- The solutions of a system of equations are the values of the variables that make all the equations true; a solution is represented by an ordered triple (p,q,r).
Practice Makes Perfect
Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables
In the following exercises, determine whether the ordered triple is a solution to the system.
1. {2x−6y+z=33x−4y−3z=22x+3y−2z=3
ⓐ (3,1,3)
ⓑ (4,3,7)
2. {−3x+y+z=−4−x+2y−2z=12x−y−z=−1
ⓐ (−5,−7,4)
ⓑ (5,7,4)
- Answer
-
ⓐ no ⓑ yes
3. {y−10z=−82x−y=2x−5z=3
ⓐ (7,12,2)
ⓑ (2,2,1)
4. {x+3y−z=15y=23x−2x−3y+z=−2
ⓐ (−6,5,12)
ⓑ (5,43,−3)
- Answer
-
ⓐ no ⓑ yes
Solve a System of Linear Equations with Three Variables
In the following exercises, solve the system of equations.
5. {5x+2y+z=5−3x−y+2z=62x+3y−3z=5
6. {6x−5y+2z=32x+y−4z=53x−3y+z=−1
- Answer
-
(4,5,2)
7. {2x−5y+3z=83x−y+4z=7x+3y+2z=−3
8. {5x−3y+2z=−52x−y−z=43x−2y+2z=−7
- Answer
-
(7,12,−2)
9. {3x−5y+4z=55x+2y+z=02x+3y−2z=3
10. {4x−3y+z=72x−5y−4z=33x−2y−2z=−7
- Answer
-
(−3,−5,4)
11. {3x+8y+2z=−52x+5y−3z=0x+2y−2z=−1
12. {11x+9y+2z=−97x+5y+3z=−74x+3y+z=−3
- Answer
-
(2,−3,−2)
13. {13x−y−z=1x+52y+z=−22x+2y+12z=−4
14. {x+12y+12z=015x−15y+z=013x−13y+2z=−1
- Answer
-
(6,−9,−3)
15. \left\{ \begin{array} {l} x+\dfrac{1}{3}y−2z=−1 \\ \dfrac{1}{3}x+y+\dfrac{1}{2}z=0 \\ \dfrac{1}{2}x+\dfrac{1}{3}y−\dfrac{1}{2}z=−1 \end{array} \right.
16. \left\{ \begin{array} {l} \dfrac{1}{3}x−y+\dfrac{1}{2}z=4 \\ \dfrac{2}{3}x+\dfrac{5}{2}y−4z=0 \\ x−\dfrac{1}{2}y+\dfrac{3}{2}z=2 \end{array} \right.
- Answer
-
(3,−4,−2)
17. \left\{ \begin{array} {l} x+2z=0 \\ 4y+3z=−2 \\ 2x−5y=3 \end{array} \right.
18. \left\{ \begin{array} {l} 2x+5y=4 \\ 3y−z=\dfrac{3}{4} \\ x+3z=−3 \end{array} \right.
- Answer
-
(−3,2,3)
19. \left\{ \begin{array} {l} 2y+3z=−1 \\ 5x+3y=−6 \\ 7x+z=1 \end{array} \right.
20. \left\{ \begin{array} {l} 3x−z=−3 \\ 5y+2z=−6 \\ 4x+3y=−8 \end{array} \right.
- Answer
-
(−2,0,−3)
21. \left\{ \begin{array} {l} 4x−3y+2z=0 \\ −2x+3y−7z=1 \\ 2x−2y+3z=6 \end{array} \right.
22. \left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right.
- Answer
-
no solution
23. \left\{ \begin{array} {l} 2x+3y+z=1 \\ 2x+y+z=9 \\ 3x+4y+2z=20 \end{array} \right.
24. \left\{ \begin{array} {l} x+4y+z=−8 \\ 4x−y+3z=9 \\ 2x+7y+z=0 \end{array} \right.
- Answer
-
x=\dfrac{203}{16};\space y=–\dfrac{25}{16};\space z=–\dfrac{231}{16};
25. \left\{ \begin{array} {l} x+2y+z=4 \\ x+y−2z=3 \\ −2x−3y+z=−7 \end{array} \right.
26. \left\{ \begin{array} {l} x+y−2z=3 \\ −2x−3y+z=−7 \\ x+2y+z=4 \end{array} \right.
- Answer
-
(x,y,z) where x=5z+2;\space y=−3z+1;\space z is any real number
27. \left\{ \begin{array} {l} x+y−3z=−1 \\ y−z=0 \\ −x+2y=1 \end{array} \right.
28. \left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right.
- Answer
-
(x,y,z) where x=5z−2;\space y=4z−3;\space z is any real number
Solve Applications using Systems of Linear Equations with Three Variables
In the following exercises, solve the given problem.
29. The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is twice the measure of the first angle. The third angle is twelve more than the second. Find the measures of the three angles.
30. The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is three times the measure of the first angle. The third angle is fifteen more than the second. Find the measures of the three angles.
- Answer
-
42, 50, 58
31. After watching a major musical production at the theater, the patrons can purchase souvenirs. If a family purchases 4 t-shirts, the video, and 1 stuffed animal, their total is $135.
A couple buys 2 t-shirts, the video, and 3 stuffed animals for their nieces and spends $115. Another couple buys 2 t-shirts, the video, and 1 stuffed animal and their total is $85. What is the cost of each item?
32. The church youth group is selling snacks to raise money to attend their convention. Amy sold 2 pounds of candy, 3 boxes of cookies and 1 can of popcorn for a total sales of $65. Brian sold 4 pounds of candy, 6 boxes of cookies and 3 cans of popcorn for a total sales of $140. Paulina sold 8 pounds of candy, 8 boxes of cookies and 5 cans of popcorn for a total sales of $250. What is the cost of each item?
- Answer
-
$20, $5, $10
Writing Exercises
33. In your own words explain the steps to solve a system of linear equations with three variables by elimination.
34. How can you tell when a system of three linear equations with three variables has no solution? Infinitely many solutions?
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?


