6.1: Poisson's Formula

Assume $u$ is a solution of (6.2), then, since Fourier transform is a linear mapping,

$$\widehat{u_t-\triangle u}=\hat{0}.$$

From properties of the Fourier transform, see Proposition 5.1, we have

$$\widehat{\triangle u}=\sum_{k=1}^n\widehat{\frac{\partial^2 u}{\partial x_k^2}}=\sum_{k=1}^n i^2\xi^2_k\widehat{u}(\xi),$$

provided the transforms exist. Thus we arrive at the ordinary differential equation for the Fourier transform of $u$

$$\frac{d\widehat{u}}{dt}+|\xi|^2\widehat{u}=0,$$

where $\xi$ is considered as a parameter. The solution is

$$\widehat{u}(\xi,t)=\widehat{\phi}(\xi)e^{-|\xi|^2 t}$$

since $\widehat{u}(\xi,0)=\widehat{\phi}(\xi)$. From Theorem 5.1 it follows

$$\begin{eqnarray*} u(x,t)&=&(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ \widehat{\phi}(\xi)e^{-|\xi|^2t}e^{i\xi\cdot x}\ d\xi\\ &=&(2\pi)^{-n}\int_{\mathbb{R}^n}\ \phi(y)\left(\int_{\mathbb{R}^n}e^{i\xi\cdot (x-y)-|\xi|^2t}\ d\xi\right)\ dy. \end{eqnarray*}$$

Set

$$K(x,y,t)=(2\pi)^{-n}\int_{\mathbb{R}^n}e^{i\xi\cdot (x-y)-|\xi|^2t}\ d\xi.\]

By the same calculations as in the proof of Theorem 5.1, step (vi), we find

$$\begin{equation} \label{kernel1} K(x,y,t)=(4\pi t)^{-n/2}e^{-|x-y|^2/4t}. \end{equation}$$

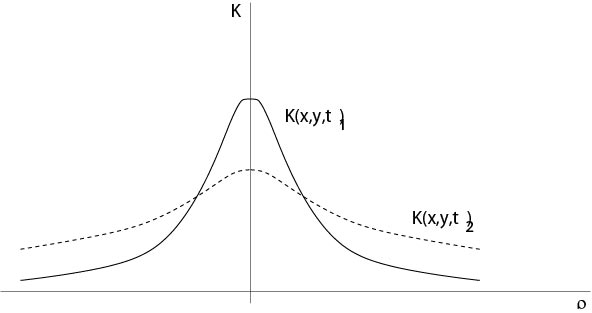
Figure 6.1.1: Kernel $K(x,y,t)$, $\rho=|x-y|$, $t_1<t_2$

Thus we have

$$\begin{equation} \label{poisson1} u(x,t)=\frac{1}{\left(2\sqrt{\pi t}\right)^n}\int_{\mathbb{R}^n}\ \phi (z)e^{-|x-z|^2/4t}\ dz. \end{equation}$$

Definition. Formula ($\ref{poisson1}$) is called Poisson's formula} and the function $K$ defined by ($\ref{kernel1}$) is called heat kernel or fundamental solution of the heat equation.

Proposition 6.1 The kernel $K$ has following properties:

1. (i) $K(x,y,t)\in C^\infty(\mathbb{R}^n\times\mathbb{R}^n\times\mathbb{R}^1_+)$,
2. (ii) $(\partial/\partial t\ -\triangle)K(x,y,t)=0,\ t>0$,
3. (iii) $K(x,y,t)>0,\ t>0$,
4. (iv) $\int_{\mathbb{R}^n}\ K(x,y,t)\ dy=1$, $x\in\mathbb{R}^n$, $t>0$
5. $\delta>0$:(v) For each fixed

$$\lim_{\begin{array}{l}t\to0\\ t>0\end{array}}\int_{\mathbb{R}^n\setminus B_\delta(x)}\ K(x,y,t)\ dy=0$$

uniformly for $x\in\mathbb{R}$.

Proof. (i) and (iii) are obviously, and (ii) follows from the definition of $K$. Equations (iv) and (v) hold since

$$\begin{eqnarray*} \int_{\mathbb{R}^n\setminus B_\delta(x)}\ K(x,y,t)\ dy&=& \int_{\mathbb{R}^n\setminus B_\delta(x)}\ (4\pi t)^{-n/2}e^{-|x-y|^2/4t}\ dy\\ &=&\pi^{-n/2}\int_{\mathbb{R}^n\setminus B_{\delta/\sqrt{4t}}(0)}e^{-|\eta|^2}\ d\eta \end{eqnarray*}$$
by using the substitution $y=x+(4t)^{1/2}\eta$. For fixed $\delta>0$ it follows (v) and for $\delta:=0$ we obtain (iv).

$\Box$

Theorem 6.1. Assume $\phi\in C(\mathbb{R}^n)$ and $\sup_{\mathbb{R}^n}|\phi(x)|<\infty$. Then $u(x,t)$ given by Poisson's formula ($\ref{poisson1}$) is in $C^{\infty}(\mathbb{R}^n\times\mathbb{R}^1_+)$, continuous on $\mathbb{R}^n\times[0,\infty)$ and a solution of the initial value problem (6.2), (6.3).

Proof. It remains to show

$$
\lim_{$$\begin{array}{l}x\to\xi\\ t\to0\end{array}$$}u(x,t)=\phi(\xi).
\]

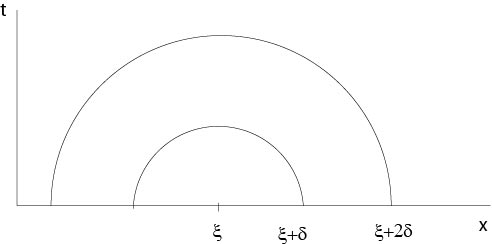
Figure 6.1.2: Figure to the proof of Theorem 6.1

Since $\phi$ is continuous there exists for given $\varepsilon>0$ a $\delta=\delta(\varepsilon)$ such that $|\phi(y)-\phi(\xi)|<\varepsilon$ if $|y-\xi|<2\delta$.
Set $M:=\sup_{\mathbb{R}^n}|\phi(y)|$. Then, see Proposition 6.1,
$$u(x,t)-\phi(\xi)=\int_{\mathbb{R}^n}\ K(x,y,t)\left(\phi(y)-\phi(\xi)\right)\ dy.$$
It follows, if $|x-\xi|<\delta$ and $t>0$, that
$$\begin{eqnarray*} |u(x,t)-\phi(\xi)|&\le&\int_{B_{\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &&+\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &\le&\int_{B_{2\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &&+2M\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\ dy\\ &\le&\varepsilon\int_{\mathbb{R}^n}\ K(x,y,t)\ dy+2M\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\ dy\\ &<&2\varepsilon \end{eqnarray*}$$
if $0<t\le t_0$, $t_0$ sufficiently small.

$\Box$

Remarks. 1. Uniqueness follows under the additional growth assumption
$$|u(x,t)|\le Me^{a|x|^2}\ \ \mbox{in}\ D_T,$$
where $M$ and $a$ are positive constants,
see Proposition 6.2 below.
In the one-dimensional case, one has uniqueness in the class $u(x,t)\ge 0$ in $D_T$, see [10], pp. 222.

2. $u(x,t)$ defined by Poisson's formula depends on all values $\phi(y)$, $y\in\mathbb{R}^n$. That means, a perturbation of $\phi$, even far from a fixed $x$, has influence to the value $u(x,t)$. This means that heat travels with infinite speed, in contrast to the experience.

Contributors and Attributions

• Prof. Dr. Erich Miersemann (Universität Leipzig)

• Integrated by Justin Marshall.