6.5: Black-Scholes Equation
- Page ID
- 2160
Solutions of the Black-Scholes equation define the value of a derivative, for example of a call or put option, which is based on an asset. An asset can be a stock or a derivative of it, for instance. In principle, there are infinitely many such products, for example n-th derivatives. The Black-Scholes equation for the value \(V(S,t)\) of a derivative is
\begin{equation}
\label{BS1}
V_t+\frac{1}{2}\sigma^2 S^2V_{SS}+rSV_S-rV=0\ \ \mbox{in}\ \Omega,
\end{equation}
where for a fixed \(T\), \(0<T<\infty\),
$$\Omega=\{(S,t)\in\mathbb{R}^2:\ 0<S<\infty,\ 0<t<T\}, \]
and \(\sigma\), \(r\) are positive constants. More precisely, \(\sigma\) is the volatility of the underlying asset \(S\), \(r\) is the guaranteed interest rate of a risk-free investment.
If \(S(t)\) is the value of an asset at time \(t\), then \(V(S(t),t)\) is the value of the derivative at time \(t\), where \(V(S,t)\) is the solution of an appropriate initial-boundary value problem for the Black-Scholes equation, see below.
The Black-Scholes equation follows from Ito's Lemma under some assumptions on the random function associated to \(S(t)\), see [26], for instance.
Call option
Here is \(V(S,t):=C(S,t)\), where \(C(S,t)\) is the value of the (European) call option. In this case we have following side conditions to (\ref{BS1}):
\begin{eqnarray}
\label{BSC1}
C(S,T)&=&\max\{S-E,0\}\\
\label{BSC2}
C(0,t)&=&0\\
\label{BSC3}
C(S,t)&=&S+o(S)\ \mbox{as}\ S\to\infty, \ \mbox{uniformly in}\ t,
\end{eqnarray}
where \(E\) and \(T\) are positive constants, \(E\) is the exercise price and \(T\) the expiry.
Side condition (\ref{BSC1}) means that the value of the option has no value at time \(T\) if \(S(T)\le E\), condition (\ref{BSC2}) says that it makes no sense to buy assets if the value of the asset is zero, condition (\ref{BSC3}) means that we buy assets if its value becomes large, see Figure 6.5.1, where the side conditions are indicated.
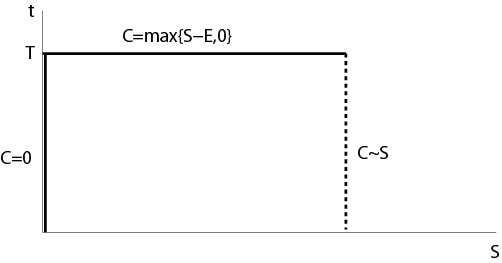
Figure 6.5.1: Side conditions for a call option
Theorem 6.4 (Black-Scholes formula for European call options).
The solution \(C(S,t)\), \(0\le S<\infty\), \(0\le t\le T\), of the initial-boundary value problem (\ref{BS1})-(\ref{BSC3}) is explicitly known and is given by
$$C(S,t)=SN(d_1)-Ee^{-r(T-t)}N(d_2),$$
where
\begin{eqnarray*}
N(x)&=&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x\ e^{-y^2/2}\ dy,\\
d_1&=&\frac{\ln(S/E)+(r+\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}},\\
d_2&=&\frac{\ln(S/E)+(r-\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}.
\end{eqnarray*}
Proof. Substitutions
$$S=Ee^x,\ \ t=T-\frac{\tau}{\sigma^2/2},\ \ C=Ev(x,\tau)\]
change equation (\ref{BS1}) to
\begin{equation}
\label{BS2}
v_\tau=v_{xx}+(k-1)v_x-kv,
\end{equation}
where
$$k=\frac{r}{\sigma^2/2}.\]
Initial condition (\ref{BS2}) implies
\begin{equation}
\label{BS3}
v(x,0)=\max\{e^x-1,0\}.
\end{equation}
For a solution of (\ref{BS2}) we make the ansatz
$$v=e^{\alpha x+\beta \tau}u(x,\tau),\]
where \(\alpha\) and \(\beta\) are constants which we will determine as follows. Inserting the ansatz into differential equation (\ref{BS2}), we get
$$\beta u+u_\tau=\alpha^2u+2\alpha u_x+u_{xx}+(k-1)(\alpha u+u_x)-ku.\]
Set \(\beta=\alpha^2+(k-1)\alpha-k\) and choose \(\alpha\) such that \(0=2\alpha+(k-1)\), then \(u_\tau=u_{xx}\). Thus
\begin{equation}
\label{BS4}
v(x,\tau)=e^{-(k-1)x/2-(k+1)^2\tau/4}u(x,\tau),
\end{equation}
where \(u(x,\tau)\) is a solution of the initial value problem
\begin{eqnarray*}
u_\tau&=&u_{xx},\ \ -\infty<x<\infty,\ \tau>0\\
u(x,0)&=&u_0(x),
\end{eqnarray*}
with
$$u_0(x)=\max\left\{e^{(k+1)x/2}-e^{(k-1)x/2},0\right\}.\]
A solution of this initial value problem is given by Poisson's formula
$$u(x,\tau)=\frac{1}{2\sqrt{\pi \tau}}\int_{-\infty}^{+\infty}\ u_0(s)e^{-(x-s)^2/(4\tau)}\ ds.\]
Changing variable by \(q=(s-x)/(\sqrt{2\tau})\), we get
\begin{eqnarray*}
u(x,\tau)&=&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\ u_0(q\sqrt{2\tau}+x)e^{-q^2/2}\ dq\\
&=&I_1-I_2,
\end{eqnarray*}
where
\begin{eqnarray*}
I_1&=&\frac{1}{\sqrt{2\pi}}\int_{-x/(\sqrt{2\tau)}}^{\infty}\ e^{(k+1)(x+q\sqrt{2\tau})}e^{-q^2/2}\ dq\\
I_2&=&\frac{1}{\sqrt{2\pi}}\int_{-x/(\sqrt{2\tau)}}^{\infty}\ e^{(k-1)(x+q\sqrt{2\tau})}e^{-q^2/2}\ dq.
\end{eqnarray*}
An elementary calculation shows that
\begin{eqnarray*}
I_1&=&e^{(k+1)x/2+(k+1)^2\tau/4}N(d_1)\\
I_2&=&e^{(k-1)x/2+(k-1)^2\tau/4}N(d_2),
\end{eqnarray*}
where
\begin{eqnarray*}
d_1&=&\frac{x}{\sqrt{2\tau}}+\frac{1}{2}(k+1)\sqrt{2\tau}\\
d_2&=&\frac{x}{\sqrt{2\tau}}+\frac{1}{2}(k-1)\sqrt{2\tau}\\
N(d_i)&=&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{d_i}\ e^{-s^2/2}\ ds,\ \ i=1,\ 2.
\end{eqnarray*}
Combining the formula for \(u(x,\tau)\), definition (\ref{BS4}) of \(v(x,\tau)\) and the previous settings \(x=\ln(S/E)\), \(\tau=\sigma^2(T-t)/2\) and \(C=Ev(x,\tau)\), we get finally the formula of Theorem 6.4.
In general, the solution \(u\) of the initial value problem for the heat equation is not uniquely defined, see for example [10], pp. 206.
Uniqueness. The uniqueness follows from the growth assumption (\ref{BSC3}). Assume there are two solutions of (\ref{BS1}), (\ref{BSC1})-(\ref{BSC3}), then the difference \(W(S,t)\) satisfies the differential equation (\ref{BS1}) and the side conditions
$$W(S,T)=0,\ W(0,t)=0,\ W(S,t)=O(S)\ \mbox{as}\ S\to\infty\]
uniformly in \(0\le t\le T\).
From a maximum principle consideration, see an exercise, it follows that \(|W(S,t)|\le cS\) on \(S\ge 0\), \(0\le t\le T\). The constant \(c\) is independent of \(S\) and \(t\). From the definition of \(u\) we see that
$$
u(x,\tau)=\frac{1}{E}e^{-\alpha x-\beta\tau} W(S,t),
$$
where \(S=Ee^x\), \(t=T-2\tau/(\sigma^2)\). Thus we have the growth property
\begin{equation}
\label{wachs1}
|u(x,\tau)|\le Me^{a|x|},\ \ x\in\mathbb{R}^1,
\end{equation}
with positive constants \(M\) and \(a\). Then the solution of \(u_\tau=u_{xx}\), in \(-\infty<x<\infty\),
\(0\le\tau\le\sigma^2 T/2\), with the initial condition \(u(x,0)=0\) is uniquely defined in the class of functions satisfying the growth condition (\ref{wachs1}), see Proposition 6.2 of this chapter.
That is, \(u(x,\tau)\equiv 0\).
\(\Box\)
Put option
Here is \(V(S,t):=P(S,t)\), where \(P(S,t)\) is the value of the (European) put option. In this case we have following side conditions to (\ref{BS1}):
\begin{eqnarray}
\label{BSP1}
P(S,T)&=&\max\{E-S,0\}\\
\label{BSP2}
P(0,t)&=&Ee^{-r(T-t)}\\
\label{BSP3}
P(S,t)&=&o(S)\ \mbox{as}\ S\to\infty,\ \mbox{uniformly in}\ 0\le t\le T.
\end{eqnarray}
Here \(E\) is the exercise price and \(T\) the expiry.
Side condition (\ref{BSP1}) means that the value of the option has no value at time \(T\) if \(S(T)\ge E\), condition (\ref{BSP2}) says that it makes no sense to sell assets if the value of the asset is zero, condition (\ref{BSP3}) means that it makes no sense to sell assets if its value becomes large.
Theorem 6.5 (Black-Scholes formula for European put options).
The solution \(P(S,t)\), \(0<S<\infty\), \(t<T\) of the initial-boundary value problem (\ref{BS1}), (\ref{BSP1})-(\ref{BSP3}) is explicitly known and is given by
$$P(S,t)=Ee^{-r(T-t)}N(-d_2)-SN(-d_1)$$
where \(N(x)\), \(d_1\), \(d_2\) are the same as in Theorem 6.4.
Proof. The formula for the put option follows by the same calculations as in the case of a call option or from the put-call parity
$$C(S,t)-P(S,t)=S-Ee^{-r(T-t)}\]
and from
$$N(x)+N(-x)=1.\]
Concerning the put-call parity see an exercise. See also [26], pp. 40, for a heuristic argument which leads to the formula for the put-call parity.
\(\Box\)
Contributors and Attributions
Integrated by Justin Marshall.


