1.7: Structures
- Page ID
- 9684
Let us, by way of example, return to the language \(\mathcal{L}_{NT}\) of number theory. Recall that \(\mathcal{L}_{NT}\) is \(\{ 0, S, +, \cdot, E, <\}\), where 0 is a constant symbol, \(S\) is a unary function symbol, \(+\), \(\cdot\), and \(E\) are binary function symbols, and \(<\) is a binary relation symbol. We now want to discuss the possible mathematical structures in which we can interpret these symbols, and thus the formulas and sentences of \(\mathcal{L}_{NT}\).
"But wait!" cries the incredulous reader. "You just said that this is the language of number theory, so certainly we already know what each of those symbols means."
It is certainly the case that you know an interpretation for these symbols. The point of this section is that there are many different possible interpretations for these symbols, and we want to be able to specify which of those interpretations we have in mind at any particular moment.
Probably the interpretation you had in mind (what we will call the standard model for number theory) works with the set of natural numbers \(\{ 0, 1, 2, 3, \ldots \}\). The symbol 0 stands for the number 0.
Chaff: Carefully, now! The symbol 0 is the mark on the paper, the numeral. The number 0 is the thing that the numeral 0 represents. The numeral is something that you can see. The number is something that you cannot see.
The symbol \(S\) is a unary function symbol, and the function for which that symbol stands is the successor function that maps a number to the next larger natural number. The symbols \(+\), \(\cdot\), and \(E\) represent the functions of addition, multiplication, and exponentiation, and the symbol \(<\) will be used for the "less than" relation.
But that is only one of the ways that we might choose to interpret those symbols. Another way to interpret all of those symbols would be to work with the numbers 0 and 1, interpreting the symbol 0 as the number 0, \(S\) as the function that maps 0 and 1 and 1 to 0, \(+\) as addition mod 2, \(\cdot\) as multiplication mod 2, and (just for variety) \(E\) as the function with constant value 1. The symbol \(<\) can still stand for the relation "less than".
Or, if we were in a slightly more bizarre mood, we could work in a universe consisting of Beethoven, Picasso, and Ernie Banks, interpreting the symbol 0 as Picasso, \(S\) as the identity function, \(<\) as equality, and each of the binary function symbols as the constant function with output Ernie Banks.
The point is that there is nothing sacred about one mathematical structure as opposed to another. Without determining the structure under consideration, without deciding how we wish to interpret the symbols of the language, we have no way of talking about the truth or falsity of a sentence as trivial as
\[\left( \forall v_1 \right) \left( v_1 < S \left( v_1 \right) \right).\]
Definition 1.6.1. Fix a language \(\mathcal{L}\). An \(\mathcal{L}\)-structure \(\mathfrak{A}\) is a nonempty set \(A\), called the universe of \(\mathfrak{A}\), together with:
- For each constant symbol \(c\) of \(\mathcal{L}\), an element \(c^\mathfrak{A}\) of \(A\),
- For each \(n\)-ary function symbol \(f\) of \(\mathcal{L}\), a function \(f^\mathfrak{A} : A^n \rightarrow A\), and
- For each \(n\)-ary relation symbol \(R\) of \(\mathcal{L}\), an \(n\)-ary relation \(R^\mathfrak{A}\) on \(A\) (i.e., a subset of \(A^n\)).
Notice that the domain of the function \(f^\mathfrak{A}\) is the set \(A^n\), so \(f^\mathfrak{A}\) is defined for all elements of \(A^n\). Later in the text we will have occasion to discuss partial functions, those whose domain in a proper subset of \(A^n\), but for now our functions are total functions, defined on all of the advertised domain.
Chaff: The letter \(\mathfrak{A}\) is a German Frakture capital A. We will also have occasion to use \(\mathfrak{A}\)'s friends, \(\mathfrak{B}\) and \(\mathfrak{C}\). \(\mathfrak{N}\) will be used for a particular structure involving the natural numbers. The use of this typeface is traditional (which means this is the way we learned it). For your handwritten work, probably using capital script letters will be the best.
Often, we will write a structure as an ordered \(k\)-tuple, like this:
\[\mathfrak{A} = \left( A, c_1^\mathfrak{A}, c_2^\mathfrak{A}, f_1^\mathfrak{A}, R_1^\mathfrak{A}, R_2^\mathfrak{A} \right).\]
As you can see, the notation is starting to get out of hand once again, and we will not hesitate to simplify and abbreviate when we believe that we can do so without confusion. So, when we are working in \(\mathcal{L}_{NT}\), we will often talk about the standard structure
\[\mathfrak{N} = \left( \mathbb{N}, 0, S, +, \cdot, E, < \right),\]
where the constants, functions, and relations do not get the superscripts they deserve, and the authors trust that you will interpret \(\mathbb{N}\) as the collection \(\{0, 1, 2, \ldots \}\) of natural numbers, the symbol 0 to stand for the number 0, \(+\) to stand for addition, \(S\) to stand for the successor function, and so on. By the way, if you are not used to thinking of 0 as a natural number, do not panic. Set theorists see 0 as the most natural of objects, so we tend to include it in \(\mathbb{N}\) without thinking about it.
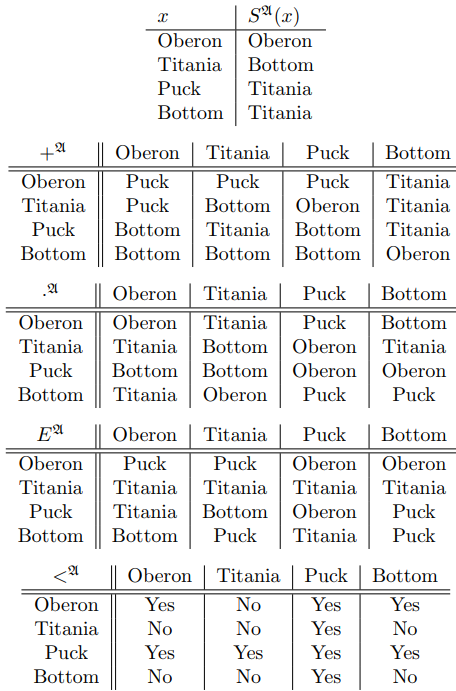
Table 1.1: A Midsummer Night's Structure
Example 1.6.2. The structure \(\mathfrak{N}\) that we have just introduced is called the standard \(\mathcal{L}_{NT}\)-structure. To emphasize that there are other perfectly good \(\mathcal{L}_{NT}\)-structures, let us construct a different \(\mathcal{L}_{NT}\)-structure \(\mathfrak{A}\) with exactly four elements. The elements of \(A\) will be Oberon, Titania, Puck, and Bottom. The constant \(0^\mathfrak{A}\) will be Bottom. Now we have to construct the functions and relations for our structure. As everything is unary or binary, setting forth tables (as in Table 1.1) seems a reasonable way to proceed. So you can see that in this structure \(\mathfrak{A}\) that Titania \(+\) Puck \(=\) Oberon, while Puck \(+\) Titania \(=\) Titania. You can also see that 0 (also known as Bottom) is not the additive identity in this structure, and that \(<\) is a very strange ordering.
Now the particular functions and relation that we chose were just the functions and relations that jumped into Chris's fingers as he typed up this example, but any such functions would have worked perfectly well to define an \(\mathcal{L}_{NT}\)-structure. It may well be worth your while to figure out if this \(\mathcal{L}_{NT}\)-sentence is true (whatever that means) in \(\mathfrak{A}\): \(SS0 + SS0 < SSSSS0E0 + S0\).
Example 1.6.3. We work in a language with one constant symbol, \(\mathfrak{L}\), and one unary function symbol, \(X\). So, to define a model \(\mathfrak{A}\), all we need to do is specify a universe, an element of the universe, and a function \(X^\mathfrak{A}\). Suppose that we let the universe be the collection of all finite strings of 0 or more capital letters from the Roman alphabet. So \(A\) includes such strings as: BABY, LOGICISBETTERTHANSIX, \(\varepsilon\) (the empty string), and DLKFDFAHADS. The constant symbol \(\mathfrak{L}\) will be interpreted as the string POTITION, and the function \(X^\mathfrak{A}\) is the function that adds an X to the beginning of a string. so \(X^\mathfrak{A}\)(YLOPHONE) \(=\) XYLOPHONE. Convince yourself that this is a valid, if somewhat odd, \(\mathcal{L}\)-structure.
To try to be clear about things, notice that we have \(X\), the function symbol, which is an element of the language \(\mathcal{L}\). Then there is X, the string of exactly one capital letter of the Roman alphabet, which is one of the elements of the universe. (Did you notice the change in typeface without our pointing it out? You may have a future in publishing!)
Let us look at one of the terms of the language: \(X \mathfrak{L}\). In our particular \(\mathcal{L}\)-structure \(\mathfrak{A}\) we will interpret this as
\[X^\mathfrak{A} \left( \mathfrak{L}^\mathfrak{A} \right) = X^\mathfrak{A} \left( \text{POTITION} \right) = \text{XPOTITION}.\]
In a different structure, \(\mathfrak{B}\), it is entirely possible that the interpretation of the term \(X \mathfrak{L}\) will be HUNNY or AARDVARK or \(3 \pi / 17\). Without knowing the structure, without knowing how to interpret the symbols of the language, we cannot begin to know what object is referred to by a term.
Chaff: All of this stuff about interpreting terms in a structure will be made formal in the next section, so don't panic if it doesn't all make sense right now.
What makes this example confusing, as well as important, is that the function symbol is part of the structure for the language and (modulo a superscript and a change in typeface) the function acts on the elements of the structure in the same way that the function symbol is used in creating \(\mathcal{L}\)-formulas.
Example 1.6.4. Now, let \(\mathcal{L}\) be \(\{0, f, g, R\}\), where 0 is a constant symbol, \(f\) is a unary function symbol, \(g\) is a binary function symbol, and \(R\) is a 3-ary relation symbol. We define an \(\mathcal{L}\)-structure \(\mathfrak{B}\) as follows: \(B\), the universe, is the set of all variable-free \(\mathcal{L}\)-terms. The constant \(0^\mathfrak{B}\) is the term 0. The functions \(f^\mathfrak{B}\) and \(g^\mathfrak{B}\) are defined as in Example 1.6.3, so if \(t\) and \(s\) are elements of \(B\), (i.e., variable-free terms), then \(f^\mathfrak{B} \left( t \right)\) is \(ft\) and \(g^\mathfrak{B} \left( t, s \right)\) is \(gts\).
Let us look at this in a little more detail. Consider 0, the constant symbol, which is an element of \(\mathcal{L}\). Since 0 is a constant symbol, it is a term, so 0 is an element of \(B\), the universe of our structure \(\mathfrak{B}\). (Alas, there is no change in typeface to help us out this time.) If we want to see what element of the universe is referred to by the constant symbol 0, we see that \(0^\mathfrak{B} = 0\), so the term 0 refers to the element of the universe 0.
If we look at another term of the language, say \(f0\), and we try to find the element of the universe that is denoted by this term, we find that it is
\[f^\mathfrak{B} \left( 0^\mathfrak{B} \right) = f^\mathfrak{B} \left( 0 \right) = f0.\]
So the term \(f0\) denotes an element of the universe, and that element of the universe is ... \(f0\). This is pretty confusing, but all that is going on is that the elements of the universe are the syntactic objects of the language.
This sort of structure is called a Henkin structure, after Leon Henkin, who introduced them in his PhD dissertation in 1949. These structures will be crucial in our proof of the Completeness Theorem in Chapter 3. The proof of that theorem will involve the construction of a particular mathematical structure, and the structure that we will build will be a Henkin structure.
To finish building our structure \(\mathfrak{B}\), we have to define a relation \(R^\mathfrak{B}\). As \(R\) is a 3-ary relation symbol, \(R^\mathfrak{B}\) is a subset of \(B^3\). We will arbitrarily define
\[R^\mathfrak{B} = \{ \left( r, s, t \right) \in B^3 \: | \: \text{the number of function symbols in } r \: \text{is even} \}.\]
This finishes defining the structure \(\mathfrak{B}\). The definition of \(R^\mathfrak{B}\) given is entirely arbitrary. We invite you to come up with a more interesting or more humorous definition on your own.
Exercises
- Consider the structure constructed in Example 1.6.2. Find the value of each of the following: \(0 + 0\), \(0E0\), \(S0 \cdot SS0\). Do you think \(0 < 0\) is true in this structure?
- Suppose that \(\mathcal{L}\) is the language \(\{0, +, <\}\). Let's work together to describe an \(\mathcal{L}\)-structure \(\mathfrak{A}\). Let the universe \(A\) be the set consisting of all of the natural numbers together with Ingrid Bergman and Humphrey Bogart. You decide on the interpretations of the symbols. What is the value of \(5 +\) Ingrid? Is Bogie \(< 0\)?
- Here is a language consisting of one constant symbol, one 3-ary function symbol, and one binary relation symbol: \(\mathcal{L}\) is \(\{\flat, \sharp, \natural\}\). Describe an \(\mathcal{L}\)-model that has as its universe \(\mathbb{R}\), the set of real numbers. Describe another \(\mathcal{L}\)-model that has a finite universe.
- Write a short paragraph explaining the difference between a language and a structure for a language.
- Suppose that \(\mathfrak{A}\) and \(\mathfrak{B}\) are two \(\mathcal{L}\)-structures. We will say that \(\mathfrak{A}\) and \(\mathfrak{B}\) are isomorphic and write \(\mathfrak{A} \cong \mathfrak{B}\) if there is a bijection \(i : A \rightarrow B\) such that for each constant symbol \(c\) of \(\mathcal{L}\), \(i \left( c^\mathfrak{A} \right) = c^\mathfrak{B}\), for each \(n\)-ary function symbol \(f\) and for each \(a_1, \ldots, a_n \in A\), \(i \left( f^\mathfrak{A} \left( a_1, \ldots, a_n \right) \right) = f^\mathfrak{B} \left( i \left( a_1 \right), \ldots i \left( a_n \right) \right)\), and for each \(n\)-ary relation symbol \(R\) in \(\mathcal{L}\), \(\left( a_1, \ldots a_n \right) \in R^\mathfrak{A}\) if and only if \(\left( i \left( a_1 \right), \ldots, i \left( a_n \right) \right) \in R^\mathfrak{B}\). The function \(i\) is called an isomorphism.
(a) Show that \(\cong\) is an equivalence relation. [Suggestion: This means that you must show that the relation \(\cong\) is reflexive, symmetric, and transitive. To show that \(\cong\) is reflexive, you must show that for any structure \(\mathfrak{A}\), \(\mathfrak{A} \cong \mathfrak{A}\), which means that you must find an isomorphism, a function, mapping \(A\) to \(A\) that satisfies the conditions above. So the first line of your proof should be, "Consider this function, with domain \(A\) and codomain \(A : i \left( x \right) =\) [something brilliant]." Then show that your function \(i\) is an isomorphism. Then show, if \(\mathfrak{A} \cong \mathfrak{B}\), then \(\mathfrak{B} \cong \mathfrak{A}\). Then tackle transitivity. In each case, you must define a particular function and shown that your function is an isomorphism.]
(b) Find a new structure that is isomorphic to the structure given in Example 1.6.2. Prove that the structures are isomorphic.
(c) Find two different structures for a particular language and prove that they are not isomorphic.
(d) Find two different structures for a particular language such that the structures have the same number of elements in their universes but they are still not isomorphic.Prove they are not isomorphic. - Take the language of Example 1.6.4 and let \(C\) be the set of all \(\mathcal{L}\)-terms. Create an \(\mathcal{L}\)-structure \(\mathfrak{C}\) by using this universe in such a way that the interpretation of a term \(t\) is not equal to \(t\).
- If we take the language \(\mathcal{L}_{NT}\), we can create a Henkin structure for that language in the same way as in Example 1.6.4. Do so. Consider the \(\mathcal{L}_{NT}\)-formula \(S0 + S0 = SS0\). Is this formula "true" (whatever that means) in your structure? Justify your answer.


