8.4: Transitivity
( \newcommand{\kernel}{\mathrm{null}\,}\)
Small group theorists argue that many of the most interesting and basic questions of social structure arise with regard to triads. Triads allow for a much wider range of possible sets of relations.
With undirected data, there are four possible types of triadic relations (no ties, one tie, two ties, or all three ties). Counts of the relative prevalence of these four types of relations across all possible triples (that is, a "triad census") can give a good sense of the extent to which a population is characterized by "isolation", "couples only", "structural holes" (i.e. where one actor is connected to two others, who are not connected to each other), or "clusters". UCINET does not have a routine for conducting triad censuses (see Pajek, which does).
With directed data, there are actually 16 possible types of relations among 3 actors, including relationships that exhibit hierarchy, equality, and the formation of exclusive groups (e.g. where two actors connect, and exclude the third). Thus, small group researchers suggest all of the really fundamental forms of social relationships can be observed in triads. Because of this interest, we may wish to conduct a "triad census" for each actor, and for the network as a whole (again, see Pajek).
In particular, we may be interested in the proportion of triads that are "transitive" (that is, display a type of balance where, if A directs a tie to B, and B directs a tie to C, then A also directs a tie to C). Such transitive or balanced triads are argued by some theorists to be the "equilibrium" or natural state toward which triadic relationships tend (not all theorists would agree!).
Of the 16 possible types of directed triads, six involve zero, one, or two relations - and can't display transitivity because there are not enough ties to do so. One type with 3 relations (AB, BC, CB) does not have any ordered triples (AB, BC) and hence can't display transitivity. In three more types of triads, there are ordered triples (AB, BC) but the relation between A and C is not transitive. The remaining types of triads display varying degrees of transitivity.
UCINET does not have extensive algorithms for examining full triad censuses and building more complex models based on them (e.g. balance, clusterability, ranked clusters). A more extended treatment of this approach, with supporting software is available from Pajek. Nonetheless, the Network>Cohesion>Transitivity algorithms in UCINET offer some interesting and flexible approaches to characterizing the transitivity of triads in populations. A typical dialog is shown in Figure 8.6.
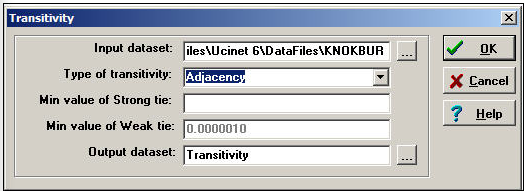
Figure 8.6: Dialog of Network>Cohesion>Transitivity
The Knoke information network is a binary, directed graph. For data of this type, the default definition of transitivity (i.e "Adjacency") is a reasonable approach. This means that we will count the number of times that, if we see AB and BC, we also see AC.
Network>Cohesion>Transitivity also provides some alternative definitions of what it means for a triad to be transitive which are useful for valued data.
A strong transitivity is one in which there are connections AB, BC, and AC, and the connection AC is stronger than the Min value of Strong tie. A weak transitivity is one in which there are connections AB, BC, and AC, and the value of AC is less than the threshold for a strong tie, but greater than the threshold Min value of Weak tie.
Two other methods are also available. A Euclidean transitivity is defined as a case where AB, BC, and AC are present, and AC has a value less than the sum of AB + BC. A Stochastic transitivity is defined as the case where AB, BC, and AC are present, and AC is less the the product AB * BC.
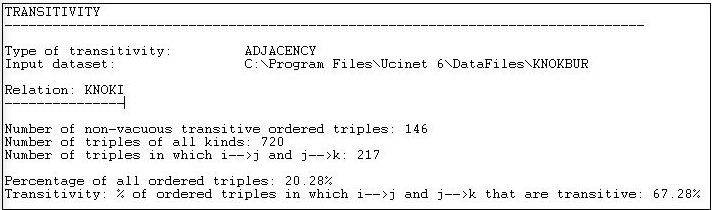
Figure 8.7: Transitivity results for Knoke information network
After performing a census of all possible triads, Network>Cohesion>Transitivity reports that it finds 146 transitive (directed) triples. That is, there are 146 cases where, if AB and BC are present, then AC is also present. There are a number of different ways in which we could try to norm this count so that it becomes more meaningful. One approach is to divide the number of transitive triads by the total number of triads of all kinds (720). This shows that


