9.3: Ego Network Density
- Page ID
- 7702
There are quite a few characteristics of the ego neighborhoods of actors that may be of interest. The Network>Ego networks>Density tools in UCINET calculate a substantial number of indexes that describe aspects of the neighborhood of each ego in a data set. Here is an example of the dialog, applied to the Knoke information exchange data (these are binary, directed connections).
Figure 9.3: Dialog for Network>Ego networks>Density
In this example, we've decided to examine "out neighborhoods" (in neighborhoods or undirected neighborhoods can also be selected). We've elected not to save the output as a dataset (if you wanted to do further analysis, or treat ego network descriptive statistics as node attributes, you might want to save the results as a file or use in other routines or Netdraw). Here are the results:
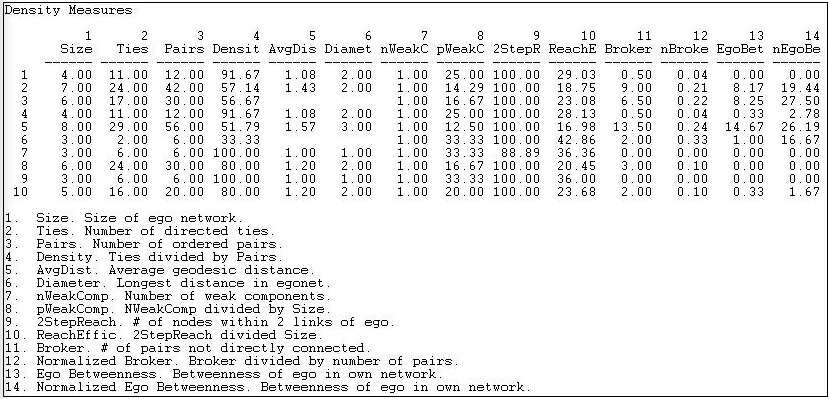
Figure 9.4: Ego network density output for Knoke information out neighborhoods
There's a lot of information here, and we should make a few comments.
Note that there is a line of data for each of the 10 organizations in the dataset. Each line describes the one-step ego neighborhood of a particular actor. Of course, many of the actors are members of many neighborhoods - so each actor may be involved in many lines of data.
- Size of ego network is the number of nodes that are one-step out neighbors of ego, plus ego itself. Actor 5 has the largest ego network; actors 6, 7, and 9 have the smallest networks.
- Number of directed ties is the number of connections among all the nodes in the ego network. Among the four actors in ego 1's network, there are 11 ties.
- Number of ordered pairs is the number of possible directed ties in each ego network. In node 1's network, there are four actors, so there are 4*3 possible directed ties.
- Density is, as the output says, the number of ties divided by the number of pairs. That is, what percentage of all possible ties in each ego network are actually present? Note that actors 7 and 9 live in neighborhoods where all actors send information to all other actors; they are embedded in very dense local structures. The welfare rights organization (node 6) lives in a small world where the members are not tightly connected. This kind of difference in the constraints and opportunities facing actors in their local neighborhoods may be very consequential.
- Average geodesic distance is the mean of the shortest path lengths among all connected pairs in the ego network. Where everyone is directly connected to everyone (e.g. nodes 7 and 9) this distance is one. In our example, the largest average path length for connected neighbors is for actor 5 (average distances among members of the neighborhood is 1.57).
- Diameter of an ego network is the length of the longest path between connected actors (just as it is for any network). The idea of a network diameter is to index the span or extensiveness of the network - how far apart the two furthest actors are. In the current example, they are not very far apart in the ego networks of most actors.
- In addition to these fairly basic and reasonably straightforward measures, the output provides some more exotic measures that get at some quite interesting ideas about ego neighborhoods that have been developed by a number of social network researchers.
- Number of weak components: A weak component is the largest number of actors who are connected, disregarding the direction of the ties (a strong component pays attention to the direction of the ties for directed data). If ego was connected to A and B (who are connected to one another), and ego is connected to C and D (who are connected to one another), but A and B are not connected in any way to C and D (except by way of everyone being connected to ego) then there would be two "weak components" in ego's neighborhood. In our example, there are no such cases - each ego is embedded in a single component neighborhood. That is, there are no cases where ego is the only connection between otherwise disjoint sets of actors.
- Number of weak components divided by size: The likelihood that there would be more than one weak component in ego's neighborhood would be a function of neighborhood size if connections were random. So, to get a sense of whether ego's role in connecting components is "unexpected" give the size of the network, it is useful to normalize the count of components by size. In our example, since there are no cases of multiple components, this is a pretty meaningless exercise.
- Two-step reach goes beyond ego's one-step neighborhood to report the percentage of all actors in the whole network that are within two directed steps of ego. In our example, only node 7 cannot get a message to all other actors within "friend-of-a-friend" distance.
- Reach efficiency (two-step reach divided by size) norms the two-step reach by dividing it by size. The idea here is: how much (non redundant) secondary contact do I get for each unit of primary contact? If reach efficiency is high, then I am getting a lot of "bang for my buck" in reaching a wider network for each unit of effort invested in maintaining a primary contact. If my neighbors, on the average, have few contacts that I don't have, I have low efficiency.
- Brokerage (number of pairs not directly connected): The idea of brokerage (more on this later) is that ego is the "go-between" for pairs of other actors. In an ego network, ego is connected to every other actor (by definition). If these others are not connected directly to one another, ego may be a "broker", that is, ego falls on the path between the others. One item of interest is simply how much potential for brokerage there is for each actor (how many times pairs of neighbors in ego's network are not directly connected). In our example, actor number 5, who is connected to almost everyone, is in a position to broker many connections.
- Normalized brokerage (brokerage divided by number of pairs) assesses the extent to which ego's role is that of broker. One can be in a brokering position a number of times, but this is a small percentage of the total possible connections in a network (e.g. the network is large). Given the large size of actor 5's network, the relative frequency with which actor 5 plays the broker is not so exceptional.
- Betweenness is an aspect of the larger concept of "centrality". A later chapter provides a more in-depth treatment of the concept and its application to whole networks. For the moment though, it's pretty easy to get the basic idea. Ego is "between" two other actors if ego lies on the shortest directed path from one to the other. The ego betweenness measure indexes the percentage of all geodesic paths from neighbor to neighbor that pass through ego.
- Normalized Betweenness compares the actual betweenness of ego to the maximum possible betweenness in a neighborhood of the size and connectivity of ego's. The "maximum" value for betweenness would be achieved when ego is the center of a "star" network; that is, no neighbors communicate directly with one another, and all directed communications between pairs of neighbors go through ego.
The ideas of "brokerage" and "betweenness" are slightly differing ways of indexing just how "central" or "powerful" ego is within their own neighborhood. This aspect of how an actor's embedding may provide them with strategic advantage has received a great deal of attention. The next two sections, on "structural holes" and "brokerage", elaborate on ways of looking at positional opportunity and constraint of individual actors.


