14.3: Linear Stability Analysis of Continuous Field Models
( \newcommand{\kernel}{\mathrm{null}\,}\)
We can apply the linear stability analysis to continuous field models. This allows us to analytically obtain the conditions for which a homogeneous equilibrium state of a spatial system loses its stability and thereby the system spontaneously forms non-homogeneous spatial patterns. Note again that the homogeneous equilibrium state discussed here is no longer a single point, but it is a straight line (or a flat plane) that covers the entire spatial domain.
Consider the dynamics of a nonlinear continuous field model
∂f∂t=F(f,∂f∂x,∂2f∂x2,…)
around its homogeneous equilibrium state feq, which satisfies
0=F(feq,0,…).
The basic approach of linear stability analysis is exactly the same as before. Namely, we will represent the system’s state as a sum of the equilibrium state and a small perturbation, and then we will determine whether this small perturbation added to the equilibrium will grow or shrink over time. Using ∆f to represent the small perturbation, we apply the following replacement
f(x,t)⇒feq+∇f(x,t)
to Equation ???, to obtain the following new continuous field model:
∂feq+∇f∂t=F(Feq+∇f,∂(feq)+∇f∂x,∂2(feq+∇f)∂x2,⋯)
∂∇f∂t=F(feq+∇f,∂∇f∂x,∂2∇f∂x2,…)
Now, look at the equation above. The key difference between this equation and the previous examples of the non-spatial models (e.g.,Equation (7.5.4)) is that the right hand side of Equation ??? contains spatial derivatives. Without them, F would be just a nonlinear scalar or vector function of f, so we could use its Jacobian matrix to obtain a linear approximation of it. But we can’t do so because of those ∂’s! We need something different to eliminate those nuisances.
In fact, we saw a similar situation before. When we discussed how to obtain analytical solutions for linear dynamical systems, the nuisances were the matrices that existed in the equations. We “destroyed” those matrices by using their eigenvectors, i.e., vectors that can turn the matrix into a scalar eigenvalue when applied to it. Can we do something similar to destroy those annoying spatial derivatives?
The answer is, yes we can. While the obstacle we want to remove is no longer a simple matrix but a linear differential operator, we can still use the same approach. Instead of using eigenvectors, we will use so-called eigenfunctions. An eigenfunction of a linear operator L is a function that satisfies
Lf=λf,
where λ is (again) called an eigenvalue that corresponds to the eigenfunction f. Look at the similarity between the definition above and the definition of eigenvectors (Equation 5.6.5)!
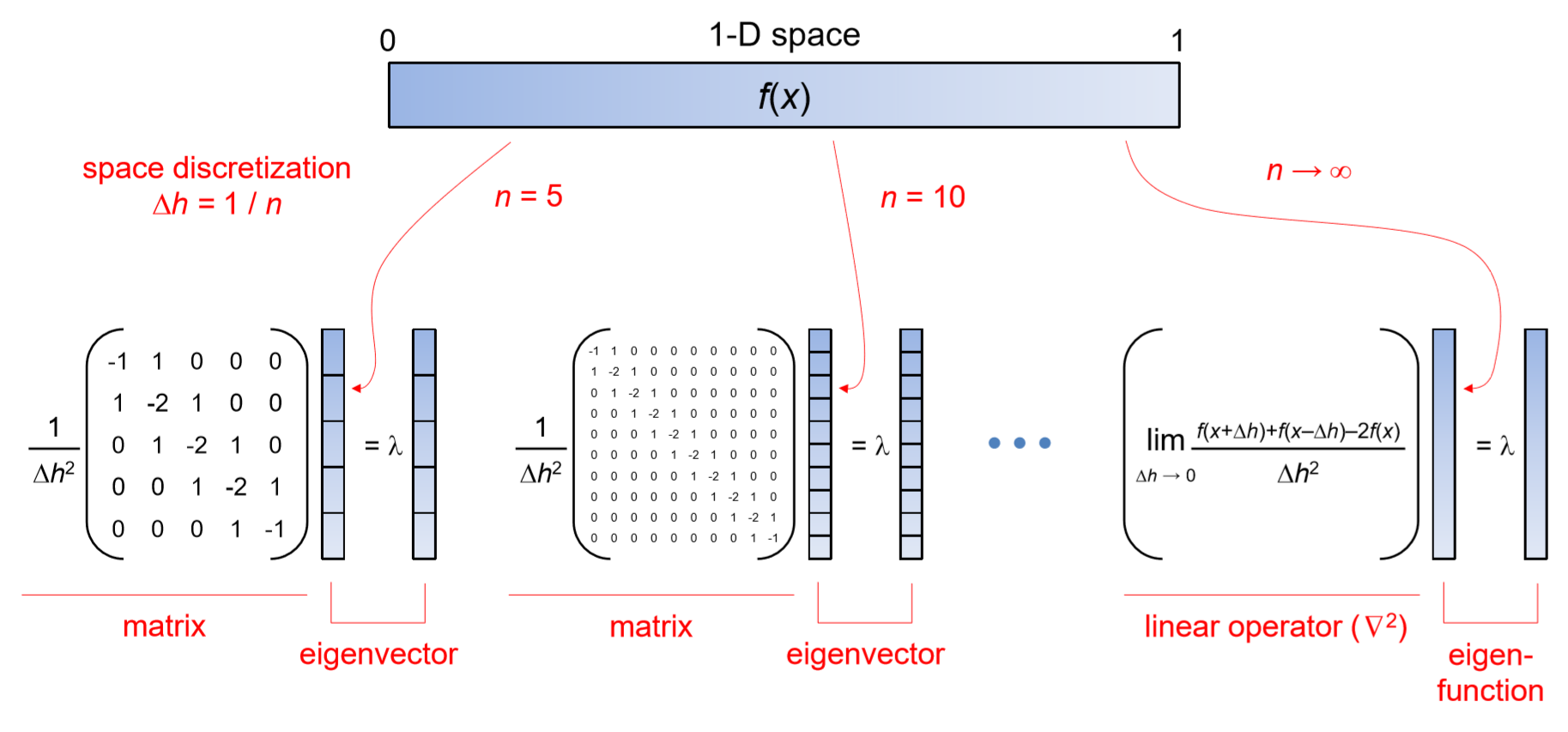
This similarity is no surprise, because, after all, the linear operators and eigenfunctions are straightforward generalizations of matrices and eigenvectors. They can be obtained by increasing the dimensions of matrices/vectors (= number of rows/columns) to infinity. Figure 14.3.1 gives a visual illustration of how these mathematical concepts are related to each other, where the second-order spatial derivative of a spatial function f(x) in a [0,1] 1-D space is shown as an example.
When the space is discretized into n compartments, the function f(x) is also defined on a discrete spatial grid made of n cells, and the calculation of its second-order spatial derivative (or, to be more precise, its discrete equivalent) can be achieved by adding its two nearest neighbors’ values and then subtracting the cell’s own value twice, as shown in Equation (13.5.11). This operation can be represented as a matrix with three diagonal lines of non-zero elements (Figure 14.3.1, left and center). Because it is a square matrix, we can calculate its eigenvalues and eigenvectors. And if the number of compartments n goes to infinity, we eventually move into the realm of continuous field models, where what used to be a matrix is now represented by a linear operator (∂2/∂x2, i.e., ∇^2 in 1-D space), while the eigenvector is now made of infinitely many numbers, which entitles it to a new name, “eigenfunction.”
In fact, this is just one instance of how mathematical concepts for matrices and vectors can be generalized to linear operators and functions in a continuous domain. Nearly all the concepts developed in linear algebra can be seamlessly extended continuous linear operators and functions, but we won’t go into details about this in this textbook.
Most linear operators we see in PDE-based continuous field models are the secondorder (and sometimes first-order) differential operators. So here are their eigenfunctions (which are nothing more than general solutions of simple linear differential equations):
- \text{For } L=\dfrac{\partial}{\partial{x}}: f(x) =Ce^{\lambda{x}}\label{(14.41)}
- \text{For } L =\dfrac{\partial^{2}}{\partial{x^{2}}}: f(x) =C_{1}e^{\sqrt{\lambda}x} +C_{2}e^{-\sqrt{\lambda}x} \label{(14.42)}
Here, λ is the eigenvalue and C, C_1, and C_2 are the constants of integration. You can confirm that these eigenfunctions satisfy Equation\ref{(14.40)} by applying L to it. So, if we use such an eigenfunction of the spatial derivative remaining in Equation \ref{(14.39)} as a small perturbation ∆f, the equation could become very simple and amenable to mathematical analysis.
There is one potential problem, though. The eigenfunctions given above are all exponential functions of x. This means that, for x with large magnitudes, these eigenfunctions could explode literally exponentially! This is definitely not a good property for a perturbation that is supposed to be “small.” What should we do? There are at least two solutions for this problem. One way is to limit the scope of the analysis to a finite domain of x (and λ, too) so that the eigenfunction remains finite without explosion. The other way is to further investigate those eigenfunctions to see if they can take a form that doesn’t show exponential divergence. Is it possible?
For Equation \ref{(14.41)}, a purely imaginary λ could make f(x) non-divergent for x →±∞, but then f(x) itself would also show complex values. This wouldn’t be suitable as a candidate of perturbations to be added to real-valued system states. But for Equation \ref{(14.42)}, there are such eigenfunctions that don’t explode exponentially and yet remain real. Try λ < 0 (i.e, √λ = ai) with complex conjugates C_1 and C_2 (i.e., C_1 = c + bi, C_2 = c−bi), and you will obtain
\begin{align} f(x) &=(c+bi)e^{iax} +(c-bi)e^{-iax} \label{(14.43)} \\[4pt] &=c(e^{iax} +e^{-iax}) +bi(e^{iax} -e^{iax})\label{(14.44)} \\[4pt] &=c(\cos{ax} +i{\sin{ax}}+\cos{(-ax)} +i\sin({-ax})) +bi(\cos{ax}+i\sin{ax}-\cos(-ax) -i\sin(-ax))\label{(14.45)} \\[4pt] &=2c\cos{ax}-2b\sin{ax}\label{(14.46)} \\[4pt] &=A(\sin{\phi})\cos{ax}-\cos{\phi}\sin{ax} \label{(14.47)} \\[4pt] &=A\sin(\phi-ax), \label{(14.48)} \end{align}
where φ = \arctan{(c/b)} and A = 2c/\sin{φ} = 2b/\cos{φ}. This is just a normal, real-valued sine wave that will remain within the range [−A,A] for any x! We can definitely use such sine wave-shaped perturbations for ∆f to eliminate the second-order spatial derivatives.
Now that we have a basic set of tools for our analysis, we should do the same trick as we did before: Represent the initial condition of the system as a linear combination of eigen-(vector or function), and then study the dynamics of each eigen-(vector or function) component separately. The sine waves derived above are particularly suitable for this purpose, because, as some of you might know, the waves with different frequencies (a in the above) are independent from each other, so they constitute a perfect set of bases to represent any initial condition.
Let’s have a walk-through of a particular example to see how the whole process of linear stability analysis works on a continuous field model. Consider our favorite Keller-Segel model:
\dfrac{\partial{a}}{\partial{t}} =\mu\nabla^{2}a -\chi\nabla \cdot(a\nabla{c}) \label{(14.49)}
\dfrac{\partial{c}}{\partial{t}} =D\nabla^{2}c +fa-kc \label{(14.50)}
The first thing we need to do is to find the model’s homogeneous equilibrium state which we will study. As you may have done this in Exercise 14.3, any a_{eq} and c_{eq} that satisfy
fa_{eq} =kc_{eq} \label{(14.51)}
can be a homogeneous equilibrium state of this model. Here we denote the equilibrium state as
(a_{eq}, c_{eq}) =(a_{eq}, \dfrac{f}{k}a_{eq}). \label{(14.52)}
Then we introduce small perturbations into this homogeneous equilibrium state, as follows:
\binom{a(x,t)}{c(x,t)} \Rightarrow \binom{a_{eq}}{\frac{f}{k}a_{eq}} +\binom{\Delta{a(x,t)}}{\Delta{x(x,t)}}. \label{(14.53)}
Here, we assume that the space is just one-dimensional for simplicity (therefore no y’s above). By applying these variable replacements to the Keller-Segel model, we obtain
\begin{align} \dfrac{\partial{\Delta{a}}}{\partial{t}} &=\mu \dfrac{\partial^{2}}{\partial{x^{2}}} (a_{eq} +\Delta{a}) -\chi\dfrac{\partial}{\partial{x}}( (a_{eq}+\Delta{a}) +\dfrac{\partial}{\partial{x}} (\dfrac{f}{x}a_{eq} + \Delta{c} )) \label{14.54} \\[4pt] &= \mu\dfrac{\partial^{2} \Delta{a}}{\partial{x^{2}}} -\chi\dfrac{\partial}{\partial{x}} (a_{eq} \dfrac{\partial{\Delta{c}}}{\partial{x}} +\Delta{a} \dfrac{\partial{\Delta{c}}}{\partial{x}}) \label{(14.55)} \\[4pt] &=\mu\dfrac{\partial^{2}\Delta{a}}{\partial{x^{2}}} -\chi{a_{eq}}\dfrac{\partial^{2} \Delta{c}}{\partial{x^{2}}} -\chi\dfrac{\partial}{\partial{x}} (\Delta{a} \dfrac{\partial{\Delta{c}}}{\partial{x}}) \label{(15.56)} \\[4pt] &=\mu \dfrac{\partial^{2}\Delta{a}}{\partial{x^{2}}} -\chi{a_{eq}} \dfrac{\partial^{2} \Delta{c}}{\partial{x^{2}}} -\chi\dfrac{\partial{\Delta{a}}}{\partial{x}}\dfrac{\partial{\Delta{c}}}{\partial{x}} -\chi\Delta{a}\dfrac{\partial^{2}\Delta{c}}{\partial{x^{2}}}, \label{(14.57)} \\[4pt] \dfrac{\partial \Delta{c}}{\partial{t}} &=D \dfrac{\partial^{2}}{\partial{x^{2}}}(\dfrac{f}{k}a_{eq} +\Delta{c} ) +f(a_{eq} +\Delta{a}) -k(\frac{f}{k}a_{eq}+\Delta{c}) \label{(14.58)} \\[4pt] &=D\dfrac{\partial^{2} \Delta{c}}{\partial{x^{2}}} + f\Delta{a} -k\Delta{c}. \label{(14.59)} \end{align}
In the equations above, both the second-order and first-order spatial derivatives remain. We can’t find an eigenfunction that eliminates both simultaneously, so let’s adopt sine waves, i.e., the eigenfunction for the second-order spatial derivatives that appear more often in the equations above, and see how the product of two first-order spatial derivatives in Equation \ref{(14.57)} responds to it. Hence, we will assume
\binom{\Delta{a}(x,t)}{\Delta{c(x,t)}} =\sin{(\omega{x})+ \phi} +\binom{\Delta{a(t)}}{\Delta{c(t)}}, \label{(14.60)}
where ω and φ are parameters that determine the spatial frequency and phase offset of the perturbation, respectively. ω/2π will give a spatial frequency (= how many waves there are per unit of length), which is called a wave number in physics. The phase offset φ doesn’t really make any difference in this analysis, but we include it anyway for the sake of generality. Note that, by adopting a particular shape of the perturbation above, we have decoupled spatial structure and temporal dynamics in Equation \ref{(14.60)} 1. Now the only dynamical variables are ∆a(t) and ∆c(t), which are the amplitudes of the sine waveshaped perturbation added to the homogeneous equilibrium state.
By plugging Equation \ref{(14.60)} into Eqs. \ref{(14.57)} and \ref{(14.59)}, we obtain the following:
\sin{(\omega{x} +\phi)} \frac{\partial{\Delta{a}}}{\partial{t}} = -\mu{\omega^{2}}{\sin{(\omega{x} +\phi)}} \Delta{a}+\chi{a_{eq}}\omega^{2}\sin{(\omega{x} +\phi)}\Delta{x} -\chi{\omega^{2}}\cos^{2}{(\omega{x} +\phi)}\Delta{a}\Delta{c} +\chi{\omega^{2}}\sin{(\omega{x}+\phi)}\Delta{a}\Delta{c} \label{(14.61)}
sin{(\omega{x}+\phi)} \dfrac{\partial{\Delta{c}}}{\partial{t}} =-D\omega^{2} \sin{(\omega{x} +\phi)} \Delta{c} +f\sin{(\omega{x} +\phi)} \Delta{a} -k\sin{(\omega{x} +\phi)} \Delta{c} \label{(14.62)}
Here, we see the product of two amplitudes (∆a∆c) in the last two terms of Equation \ref{(14.61)}, which is “infinitely smaller than infinitely small,” so we can safely ignore them to linearize the equations. Note that one of them is actually the remnant of the product of the two first-order spatial derivatives which we had no clue as to how to deal with. We should be glad to see it exiting from the stage!
After ignoring those terms, every single term in the equations equally contains \sin{(ωx+ φ)}, so we can divide the entire equations by \(\sin{(ωx + φ)} to obtain the following linear ordinary differential equations:
\dfrac{d\Delta{a}}{\partial{t}} =-\mu\omega^{2} +\chi{a_{eq}} \omega^{2} \Delta{c} \label{(14.63)}
\dfrac{d\Delta{c}}{\partial{t}} =-D\omega^{2} \Delta{c} +f\Delta{a} -k\Delta{c} \label{(14.64)}
Or, using a linear algebra notation:
\dfrac{d}{dt} \binom{\Delta{a}}{\Delta{c}} =\begin{pmatrix} -\mu\omega^{2} && \chi{a_{eq}} \omega^{2} \\ f && -D\omega^{2} -k \end{pmatrix} \binom{\Delta{a}}{\Delta{c}} \label{(14.65)}
We are finally able to convert the spatial dynamics of the original Keller-Segel model (only around its homogeneous equilibrium state) into a very simple, non-spatial linear dynamical system. What we have done is to constrain the shape of the small perturbations (i.e., deviations from the homogeneous equilibrium state) to a certain eigenfunction to eliminate spatial effects, and then ignore any higher-order terms to linearize the dynamics. Each point in this new (∆a,∆c) phase space still represents a certain spatial configuration of the original model, as illustrated in Fig. 14.3.2. Studying the stability of the origin (∆a,∆c) = (0,0) tells us if the Keller-Segel model can remain homogeneous or if it undergoes a spontaneous pattern formation.
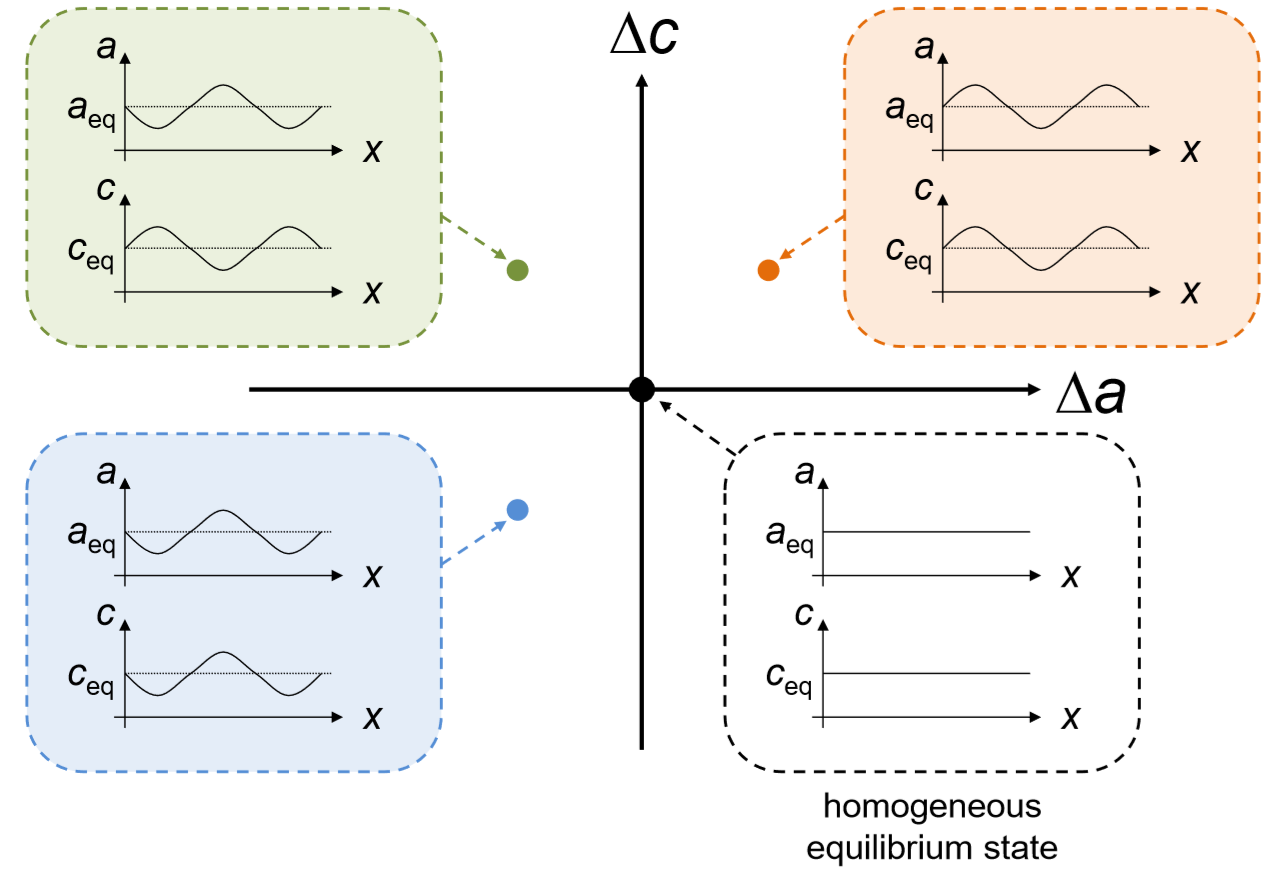
The only thing we need to do is to calculate the eigenvalues of the matrix in Equation\ref{(14.65)} and check the signs of their real parts. This may be cumbersome, but let’s get it done. Here is the calculation process, where λ is the eigenvalue of the matrix:
\begin{align} \begin{vmatrix} -\mu\omega^{2} -\lambda && \chi{a_{eq}} \omega^{2} \\ f && -D\omega^{2}-k-\lambda \end{vmatrix} &=0 \label{(14.66)} \\[4pt] (-\mu\omega^{2} -\lambda) (-D\omega^{2} -k-\lambda) -\chi{a_{eq}} \omega^{2}f &= 0 \label{(14.67)}\\[4pt] \lambda^{2} + (\mu{\omega^{2}} +D\omega^{2} +k)\lambda + \mu\omega^{2} (D\omega^{2} +k ) -\chi{a_{eq}} \omega^{2} f &=0 \label{14.68} \end{align}
\lambda =\dfrac{1}{2}(-(\mu\omega^{2} +D\omega^{2} +k) \pm \sqrt{(\mu{\omega^{2}} +D\omega^{2} +k)^{2} -4(\mu{\omega}(D{\omega^{2}} +k) -\chi{a_{eq} \omega^{2} f}) }) \label{(14.69)}
Now, the question is whether either eigenvalue’s real part could be positive. Since all the parameters are non-negative in this model, the term before “±” can’t be positive by itself. This means that the inside the radical must be positive and sufficiently large in order to make the real part of the eigenvalue positive. Therefore, the condition for a positive real part to arise is as follows:
(\mu\omega^{2} +D\omega^{2} +k) < \sqrt{(\mu{\omega^{2}} +D{\omega^{2}} +k)^{2} -4(\mu\omega^{2}(D\omega^{2} +k) -\chi{a_{eq} \omega^{2} f})} \label{(14.70)}
If this is the case, the first eigenvalue (with the “+” operator in the parentheses) is real and positive, indicating that the homogeneous equilibrium state is unstable. Let’s simplify the inequality above to get a more human-readable result:
(\mu\omega^{2} +D\omega^{2} +k)^{2} < (\mu\omega^{2} +D{\omega^{2}} +k)^{2} -4(\mu\omega^{2} 9D\omega^{2} +k) -\chi{a_{eq}\omega^{2}}f) \label{(14.71)}
0< -4(\mu\omega^{2}(D\omega^{2})+k -\chi{a_{eq}}\omega^{2}f) \label{(14.72)}
\chi{a_{eq}} \omega^{2}f > \mu\omega(D\omega^{2} +k) \label{(14.73)}
\chi{a_{eq}}f > \mu(D\omega^{2} +k) \label{(14.74)}
At last, we have obtained an elegant inequality that ties all the model parameters together in a very concise mathematical expression. If this inequality is true, the homogeneous equilibrium state of the Keller-Segel model is unstable, so it is expected that the system will show a spontaneous pattern formation. One of the benefits of this kind of mathematical analysis is that we can learn a lot about each model parameter’s effect on pattern formation all at once. From inequality \ref{(14.74)}, for example, we can make the following predictions about the aggregation process of slime mold cells (and people too, if we consider this a model of population-economy interaction):
- χ, a_eq, and f on the left hand side indicate that the aggregation of cells (or the concentration of population in major cities) is more likely to occur if
– the cells’ chemotaxis (or people’s “moneytaxis”) is stronger (χ),
– there are more cells (or people) in the system (a_eq), and/or
– the cells (or people) produce cAMP molecules (or economic values) at a faster pace (f).
- µ, D, and k on the right hand side indicate that the aggregation of cells (or the concentration of population in major cities) is more likely to be suppressed if
– the cells and cAMP molecules (or people and economic values) diffuse faster (µ and D), and/or
– the cAMP molecules (or economic values) decay more quickly (k).
It is quite intriguing that such an abstract mathematical model can provide such a detailed se of insights into the problem of urbanization (shift of population and economy from rural to urban areas), one of the critical socio-economical issues our modern society is facing today. Isn’t it?
Moreover, solving inequality \ref{(14.74)} in terms of ω^2 gives us the critical condition between homogenization and aggregation:
\dfrac{\chi{a_{eq}} f- \mu{k}}{\mu{D}} >\omega^{2} \label{(14.75)}
Note that ω can be any real number but ω^2 has to be non-negative, so aggregation occurs if and only if
\chi{a_{eq}}f > \mu{k}. \label{(14.76)}
And if it does, the spatial frequencies of perturbations that are going to grow will be given by
\dfrac{\omega}{2\pi} < \frac{1}{2\pi} \sqrt{\dfrac{\chi{a_{eq}}f -\mu{k}}{\mu{D}}}. \label{(14.77)}
The wave length is the inverse of the spatial frequency, so we can estimate the length of the growing perturbations as follows:
l =\dfrac{2\pi}{\omega} > 2\pi\sqrt{\dfrac{\mu{D}}{\chi{a_{eq}}f- \mu{k}}} =l_{c} \label{14.78}
This result means that spatial perturbations whose spatial length scales are greater than l_c are going to grow and become visible, while perturbations with length scales smaller than l_c are going to shrink and disappear. This critical length scale tells us the characteristic distance between aggregated points (or cities) spontaneously forming at the beginning of the process.
We can confirm these analytical results with numerical simulations. Figure 14.6.3 shows simulation results with µ = 10^−4, D = 10^−4, f = 1, k = 1, and a_eq = 1, while χ is varied as a control parameter. With these parameter values, inequality \ref{(14.76)} predicts that the critical value of χ above which aggregation occurs will be
\chi_{c} -\dfrac{\mu{k}}{a_{eq}f} =10^{-4}. \label{(14.79)}
which is confirmed in the simulation results perfectly.
This concludes a guided tour of the linear stability analysis of continuous field models. It may have looked rather complicated, but the key ideas are simple and almost identical to those of linear stability analysis of non-spatial models. Here is a summary of the procedure:
1. Find a homogeneous equilibrium state of the system you are interested in.
2. Represent the state of the system as a sum of the homogeneous equilibrium state and a small perturbation function.
3. Represent the small perturbation function as a product of a dynamic amplitude and a static shape of the perturbation, which is chosen to be an eigenfunction of the spatial linear operator remaining in the equation (most likely just sine waves for ∇^2).
4. Eliminate the spatial linear operator and ignore higher-order terms of small perturbations to simplify the equation into a linear non-spatial form.
5. Calculate the eigenvalues of the resulting coefficient matrix.
6. If the real part of the dominant eigenvalue is:
• Greater than 0⇒The homogeneous equilibrium state is unstable.
• Less than 0⇒The homogeneous equilibrium state is stable
. • Equal to 0 ⇒ The homogeneous equilibrium state may be neutral (Lyapunov stable).
7. In addition, if there are complex conjugate eigenvalues involved, oscillatory dynamics are going on around the homogeneous equilibrium state.
Finally, we should also note that this eigenfunction-based linear stability analysis of continuous-field models works only if the spatial dynamics are represented by a local linear differential operator (e.g., ∂f/∂x, Laplacian, etc.). Unfortunately, the same approach wouldn’t be able to handle global or nonlinear operators, which often arise in mathematical models of real-world phenomena. But this is beyond the scope of this textbook.
Add terms for population growth and decay to the first equation of the Keller-Segel model. Obtain a homogeneous equilibrium state of the revised model, and then conduct a linear stability analysis. Find out the condition for which spontaneous pattern formation occurs. Interpret the result and discuss its implications.
1In mathematical terms, this is an example of separation of variables—breaking down the original equations into a set of simpler components each of which has fewer independent variables than the original ones. PDEs for which separation of variables is possible are called separable PDEs. Our original Keller-Segel model equations are not separable PDEs, but we are trying to separate variables anyway by focusing on the dynamics around the model’s homogeneous equilibrium state and using linear approximation.


