4.12: Egyptian Fractions
- Page ID
- 10589
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consider the problem: Share 7 pies equally among 12 kids. Of course, given our model for fractions, each child is to receive the quantity “\(\frac{7}{12}\)” But this answer has little intuitive feel.
Suppose we took this task as a very practical problem. Here are the seven pies:
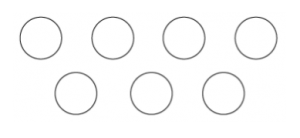
Is it possible to give each of the kids a whole pie? No.
How about the next best thing — can each child get half a pie? Yes! There are certainly 12 half pies to dole out. There is also one pie left over yet to be shared among the 12 kids. Divide this into twelfths and hand each kid an extra piece.
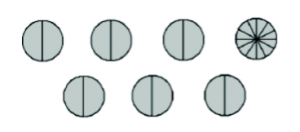
So each child gets \(\frac{1}{2} + \frac{1}{12}\) of a pie, and it is indeed true that
\[\frac{7}{12} = \frac{1}{2} + \frac{1}{12} \ldotp \nonumber \]
(Check that calculation. . . don’t just believe it!)
This seems quite reasonable. Instead of seven pieces each of size \(\frac{1}{12}\), each kid gets a piece that is \(\frac{1}{2}\) and a piece that is \(\frac{1}{12}\). It’s a lot less cutting, and a lot less messy!
1. Suppose you want to share five pies among six children, but you want each child to get a small number of (relatively) large pieces rather than five pieces of size \(\frac{1}{6}\). Following the example above, how could you do it?
- Using similar ideas, how could you share 4 pies among 7 kids?
History: Rhind Papyrus
The Egyptians (probably) were not particularly concerned with splitting up pies. But in fact, they did have a very strange (to us) way of expressing fractions. We know this by examining the Rhind Papyrus. This ancient document indicates that fractions were in use as many as four thousand years ago in Egypt, but the Egyptians seem to have worked primarily with unit fractions. They insisted on writing all of their fractions as sums of fractions with numerators equal to 1, and they insisted that the denominators of the fractions were all different.
Accurate reckoning for inquiring into things, and the knowledge of all things, mysteries…all secrets.
The Rhind Papyrus is an ancient account of Egyptian mathematics named after Alexander Henry Rhind. Rhind was a Scotsman who acquired the ancient papyrus in 1858 in Luxor, Egypt.
The papyrus dates back to around 1650 B.C. It was copied by a scribe named Ahmes (the earliest known contributor to the field of mathematics!) from a lost text written during the reign of king Amenehat III. The opening quote is taken from Ahmes introduction to the Rhind Papyrus[1]. The papyrus covers topics relating to fractions, volume, area, pyramids, and more.

Rhind Papyrus
Egyptian Fractions
To write a fraction as an Egyptian fraction, you must rewrite the fraction as:
- a sum of unit fractions (that means the numerator is 1), and
- the denominators must all be different.
The Egyptians would not write \(\frac{3}{10}\), and they would not even write \(\frac{1}{10} + \frac{1}{10} + \frac{1}{10}\). Instead, they wrote
\[\frac{1}{4} + \frac{1}{20} \ldotp \nonumber \]
The Egyptians would not write \(\frac{5}{7}\), and they would not even write \(\frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7}\). Instead, they wrote
\[\frac{1}{2} + \frac{1}{5} + \frac{1}{70} \ldotp \nonumber \]
(You should check that the sums above give the correct resulting fractions!)
Write the following as a sum of two different unit fractions. Be sure to check your answers.
\[\frac{2}{3}, \qquad \frac{2}{5}, \qquad \frac{2}{7}, \qquad \frac{2}{9} \ldotp \nonumber \]
Can you find a general rule for how to write \(\frac{2}{n}\) as an Egyptian fraction? (Assume is an odd number.)
Write the following as a sum of distinct unit fractions. (“Distinct” means the fractions must have different denominators.) Note that you may need to use more than two unit fractions in some of the sums. Be sure to check your answers.
\[\frac{3}{4}, \qquad \frac{5}{6}, \qquad \frac{3}{5}, \qquad \frac{5}{9} \ldotp \nonumber \]
Can you find a general process for fractions bigger than \(\frac{1}{2}\)?
Write the following fractions as Egyptian fractions.
\[\frac{17}{20}, \qquad \frac{3}{7} \ldotp \nonumber \]
Can you find a general algorithm that will turn any fraction at allinto an Egyptian fraction?
- Image of Rhind Papyrus from Wikimedia Commons, public domain. ↵


