9.4: Chaos in Continuous-Time Model
( \newcommand{\kernel}{\mathrm{null}\,}\)
As we reviewed above, chaos is really easy to show in discrete-time models. But the discovery of chaos was originally made with continuous-time dynamical systems, i.e., differential equations. Edward Lorenz, an American mathematician and meteorologist, and one of the founders of chaos theory, accidentally found chaotic behavior in the following model (called the Lorenz equations) that he developed to study the dynamics of atmospheric convection in the early 1960s [5]:
dxdt=s(y−x)
dydt=rx−y−xz
dzdt=xy−bz
Here s, r, and b are positive parameters.This model is known to be one of the first that can show chaos in continuous time. Let’s simulate this model with s=10, r=30, and b=3, for example:
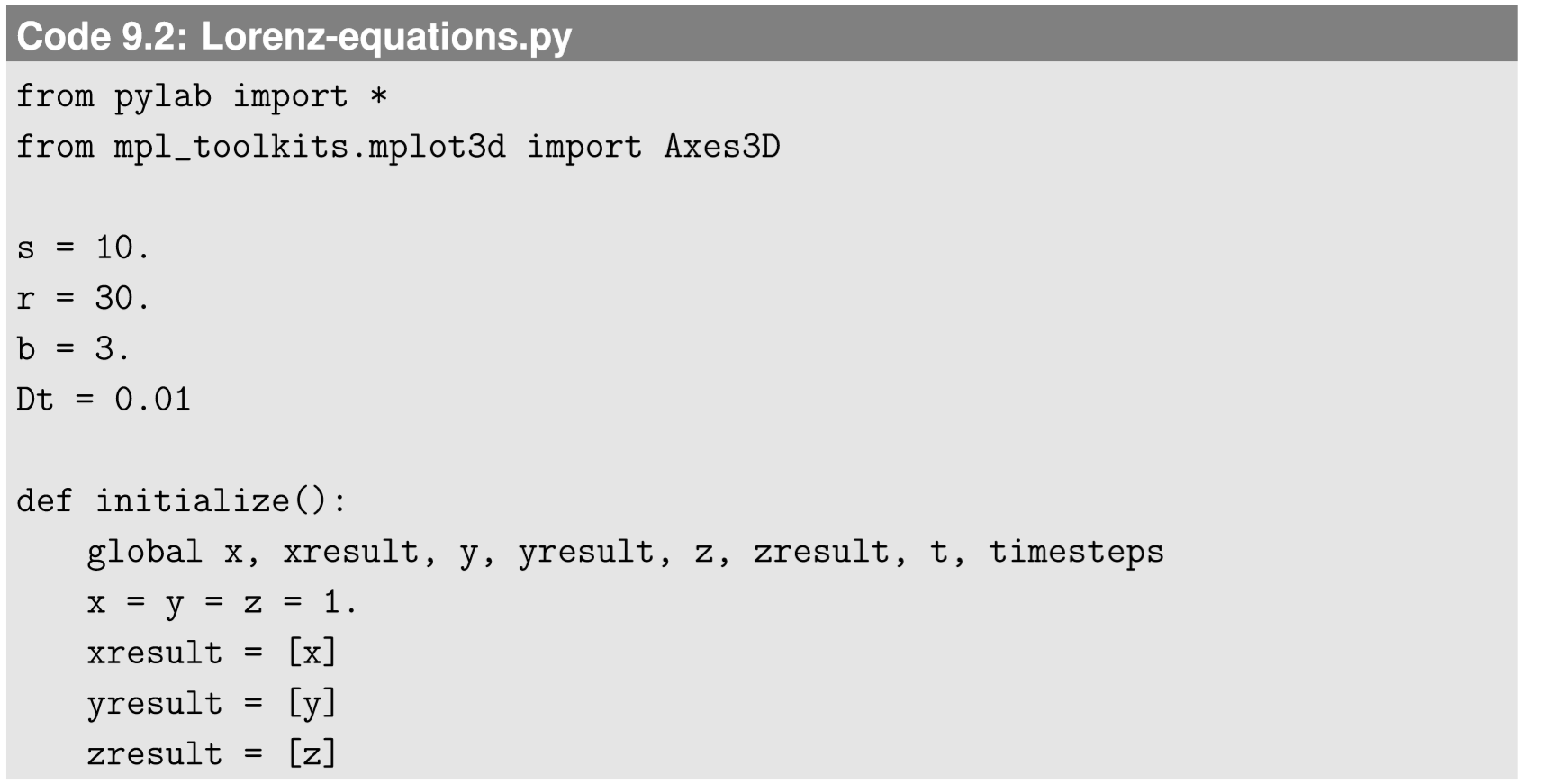




This code produces two outputs: one is the time series plots of x, y, and z (Fig. 9.4.1), and the other is the trajectory of the system’s state in a 3-D phase space (Fig. 9.4.2). As you can see in Fig. 9.4.1, the behavior of the system is highly unpredictable, but there is definitely some regularity in it too. x and y tend to stay on either the positive or negative side, while showing some oscillations with growing amplitudes. When the oscillation becomes too big, they are thrown to the other side. This continues indefinitely, with occasional switching of sides at unpredictable moments. In the meantime, z remains positive all the time, with similar oscillatory patterns.
Plotting these three variables together in a 3-D phase space reveals what is called the Lorenz attractor (Fig. 9.4.2). It is probably the best-known example of strange attractors, i.e., attractors that appear in phase spaces of chaotic systems.
Just like any other attractors, strange attractors are sets of states to which nearby trajectories are attracted. But what makes them really “strange” is that, even if they look like a bulky object, their “volume” is zero relative to that of the phase space, and thus they have a fractal dimension, i.e., a dimension of an object that is not integer-valued. For example, the Lorenz attractor’s fractal dimension is known to be about 2.06, i.e., it is pretty close to a 2-D object but not quite. In fact, any chaotic system has a strange attractor with fractal dimension in its phase space. For example, if you carefully look at the intricate patterns in the chaotic regime of Fig. 8.4.3, you will see fractal patterns there too.
Draw trajectories of the states of the Lorenz equations in a 3-D phase space for several different values of r while other parameters are kept constant. See how the dynamics of the Lorenz equations change as you vary r.
Obtain the equilibrium points of the Lorenz equations as a function of r, while keeping s=10 and b=3. Then conduct a bifurcation analysis on each equilibrium point to find the critical thresholds of r at which a bifurcation occurs.
Compare your result with numerical simulation results obtained in the previous exercise.
By the way, I said before that any chaotic system has two dynamical processes: stretching and folding. Where do these processes occur in the Lorenz attractor? It is not so straightforward to fully understand its structure, but the stretching occurs where the trajectory is circling within one of the two “wings” of the attractor. The spirals seen on those wings are unstable ones going outward, so the distance between initially close states are expanded as they circle around the spiral focus. In the meantime, the folding occurs at the center of the attractor, where two “sheets” of trajectories meet. Those two sheets actually never cross each other, but they keep themselves separated from each other, forming a “wafer sandwich” made of two thin layers, whose right half goes on to circle in the right wing while the left half goes on to the left wing. In this way, the “dough” is split into two, each of which is stretched, and then the two stretched doughs are stacked on top of each other to form a new dough that is made of two layers again. As this process continues, the final result, the Lorenz attractor, acquires infinitely many, recursively formed layers in it, which give it the name of a “strange” attractor with a fractal dimension.
Plot the Lorenz attractor in several different perspectives (the easiest choice would be to project it onto the x−y, y−z, and x−z planes) and observe its structure. Interpret its shape and the flows of trajectories from a stretching-and-folding viewpoint.
I would like to bring up one more important mathematical fact before we close this chapter:
In order for continuous-time dynamical systems to be chaotic, the dimensions of the system’s phase space must be at least 3-D. In contrast, discrete-time dynamical systems can be chaotic regardless of their dimensions
The Lorenz equations involved three variables, so it was an example of continuous-time chaotic systems with minimal dimensionality.
This fact is derived from the Poincar´e-Bendixson theorem in mathematics, which states that no strange attractor can arise in continuous 2-D phase space. An intuitive explanation of this is that, in a 2-D phase space, every existing trajectory works as a “wall” that you can’t cross, which imposes limitations on where you can go in the future. In such an increasingly constraining environment, it is not possible to maintain continuously exploring dynamics for an indefinitely long period of time.
Gather a pen and a piece of blank paper. Start drawing a continuous curve on the paper that represents the trajectory of a hypothetical dynamical system in a 2-D phase space. The shape of the curve you draw can be arbitrary, but with the following limitations:
• You can’t let the pen go off the paper. The curve must be drawn in one continuous stroke.
• The curve can’t merge into or cross itself.
• You can’t draw curves flowing in opposing directions within a very tiny area (this violates the assumption of phase space continuity).
Keep drawing the curve as long as you can, and see what happens. Discuss the implications of the result for dynamical systems. Then consider what would happen if you drew the curve in a 3-D space instead of 2-D.
Let zi denote the value of the i-th peak of z(t) produced by the Lorenz equations. Obtain time series data z1,z2,z3,... from numerical simulation results. Plot zt against zt−1, like in a cobweb plot, and see what kind of structure you find there. Do this visualization for various values of r, while keeping s=10 and b=3, and compare the results with the results of the bifurcation analysis obtained in Exercise 9.4.1.
As reviewed through this and previous chapters, bifurcations and chaos are the most distinctive characteristics of nonlinear systems. They can produce unexpected system behaviors that are often counter-intuitive to our everyday understanding of nature. But once you realize the possibility of such system behaviors and you know how and when they can occur, your view of the world becomes a more informed, enriched one. After all, bifurcations and chaos are playing important roles in our physical, biological, ecological, and technological environments (as well as inside our bodies and brains). They should thus deserve our appreciation.
This chapter concludes our journey through systems with a small number of variables. We will shift gears and finally go into the realm of complex systems that are made of a large number of variables in the next chapter.


