4.3: Multiply and Divide Fractions (Part 1)
- Page ID
- 4992
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Simplify fractions
- Multiply fractions
- Find reciprocals
- Divide fractions
Before you get started, take this readiness quiz.
- Find the prime factorization of \(48\). If you missed this problem, review Example 2.5.1.
- Draw a model of the fraction \(\dfrac{3}{4}\). If you missed this problem, review Example 4.1.2.
- Find two fractions equivalent to \(\dfrac{5}{6}\). Answers may vary. Acceptable answers include \(\dfrac{10}{12}, \dfrac{15}{18}, \dfrac{50}{60}\), etc. If you missed this problem, review Example 4.1.14.
Simplify Fractions
In working with equivalent fractions, you saw that there are many ways to write fractions that have the same value, or represent the same part of the whole. How do you know which one to use? Often, we’ll use the fraction that is in simplified form.
A fraction is considered simplified if there are no common factors, other than \(1\), in the numerator and denominator. If a fraction does have common factors in the numerator and denominator, we can reduce the fraction to its simplified form by removing the common factors.
A fraction is considered simplified if there are no common factors in the numerator and denominator.
For example,
- \(\dfrac{2}{3}\) is simplified because there are no common factors of \(2\) and \(3\).
- \(\dfrac{10}{15}\) is not simplified because \(5\) is a common factor of \(10\) and \(15\).
The process of simplifying a fraction is often called reducing the fraction. In the previous section, we used the Equivalent Fractions Property to find equivalent fractions. We can also use the Equivalent Fractions Property in reverse to simplify fractions. We rewrite the property to show both forms together.
If \(a, b, c\) are numbers where \(b ≠ 0, c ≠ 0\), then \(\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\) and \(\dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\).
Notice that \(c\) is a common factor in the numerator and denominator. Anytime we have a common factor in the numerator and denominator, it can be removed.
Step 1. Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers.
Step 2. Simplify, using the equivalent fractions property, by removing common factors.
Step 3. Multiply any remaining factors.
Simplify: \(\dfrac{10}{15}\).
Solution
To simplify the fraction, we look for any common factors in the numerator and the denominator.
| Notice that 5 is a factor of both 10 and 15. | \(\dfrac{10}{15}\) |
| Factor the numerator and denominator. | \(\dfrac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}}\) |
| Remove the common factors. | \(\dfrac{2 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}}}\) |
| Simplify. | \(\dfrac{2}{3}\) |
Simplify: \(\dfrac{8}{12}\).
- Answer
-
\(\dfrac{2}{3}\)
Simplify: \(\dfrac{12}{16}\).
- Answer
-
\(\dfrac{3}{4}\)
To simplify a negative fraction, we use the same process as in Example \(\PageIndex{1}\). Remember to keep the negative sign.
Simplify: \(− \dfrac{18}{24}\).
Solution
| We notice that 18 and 24 both have factors of 6. | \(- \dfrac{18}{24}\) |
| Rewrite the numerator and denominator showing the common factor. | \(- \dfrac{3 \cdot \textcolor{red}{6}}{4 \cdot \textcolor{red}{6}}\) |
| Remove common factors. | \(- \dfrac{3 \cdot \cancel{\textcolor{red}{6}}}{4 \cdot \cancel{\textcolor{red}{6}}}\) |
| Simplify. | \(- \dfrac{3}{4}\) |
Simplify: \(− \dfrac{21}{28}\).
- Answer
-
\(-\dfrac{3}{4}\)
Simplify: \(− \dfrac{16}{24}\).
- Answer
-
\(-\dfrac{2}{3}\)
After simplifying a fraction, it is always important to check the result to make sure that the numerator and denominator do not have any more factors in common. Remember, the definition of a simplified fraction: a fraction is considered simplified if there are no common factors in the numerator and denominator.
When we simplify an improper fraction, there is no need to change it to a mixed number.
Simplify: \(− \dfrac{56}{32}\).
Solution
| \(- \dfrac{56}{32}\) | |
| Rewrite the numerator and denominator, showing the common factors, 8. | \(- \dfrac{7 \cdot \textcolor{red}{8}}{4 \cdot \textcolor{red}{8}}\) |
| Remove common factors. | \(- \dfrac{7 \cdot \cancel{\textcolor{red}{8}}}{4 \cdot \cancel{\textcolor{red}{8}}}\) |
| Simplify. | \(- \dfrac{7}{4}\) |
Simplify: \(− \dfrac{54}{42}\).
- Answer
-
\(-\dfrac{9}{7}\)
Simplify: \(− \dfrac{81}{45}\).
- Answer
-
\(-\dfrac{9}{5}\)
Step 1. Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers.
Step 2. Simplify, using the equivalent fractions property, by removing common factors.
Step 3. Multiply any remaining factors.
Sometimes it may not be easy to find common factors of the numerator and denominator. A good idea, then, is to factor the numerator and the denominator into prime numbers. (You may want to use the factor tree method to identify the prime factors.) Then divide out the common factors using the Equivalent Fractions Property.
Simplify: \(\dfrac{210}{385}\).
Solution
| \(\dfrac{210}{385}\) | |
| Use factor trees to factor the numerator and denominator. | 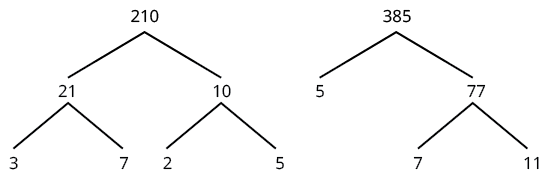 |
| Rewrite the numerator and denominator as the product of the primes. | \(\dfrac{210}{385} = \dfrac{2 \cdot 3 \cdot 5 \cdot 7}{5 \cdot 7 \cdot 11}\) |
| Remove the common factors. | \(\dfrac{2 \cdot 3 \cdot \cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}}}{\cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}} \cdot 11}\) |
| Simplify. | \(\dfrac{2 \cdot 3}{11}\) |
| Multiply any remaining factors. | \(\dfrac{6}{11}\) |
Simplify: \(\dfrac{69}{120}\).
- Answer
-
\(\dfrac{23}{40}\)
Simplify: \(\dfrac{120}{192}\).
- Answer
-
\(\dfrac{5}{8}\)
We can also simplify fractions containing variables. If a variable is a common factor in the numerator and denominator, we remove it just as we do with an integer factor.
Simplify: \(\dfrac{5xy}{15x}\).
Solution
| \(\dfrac{5xy}{15x}\) | |
| Rewrite numerator and denominator showing common factors. | \(\dfrac{5 \cdot x \cdot y}{3 \cdot 5 \cdot x}\) |
| Remove common factors. | \(\dfrac{\cancel{5} \cdot \cancel{x} \cdot y}{3 \cdot \cancel{5} \cdot \cancel{x}}\) |
| Simplify. | \(\dfrac{y}{3}\) |
Simplify: \(\dfrac{7x}{7y}\).
- Answer
-
\(\dfrac{x}{y}\)
Simplify: \(\dfrac{9a}{9b}\).
- Answer
-
\(\dfrac{a}{b}\)
Multiply Fractions
A model may help you understand multiplication of fractions. We will use fraction tiles to model \(\dfrac{1}{2} \cdot \dfrac{3}{4}\). To multiply \(\dfrac{1}{2}\) and \(\dfrac{3}{4}\), think \(\dfrac{1}{2}\) of \(\dfrac{3}{4}\).
Start with fraction tiles for three-fourths. To find one-half of three-fourths, we need to divide them into two equal groups. Since we cannot divide the three \(\dfrac{1}{4}\) tiles evenly into two parts, we exchange them for smaller tiles.
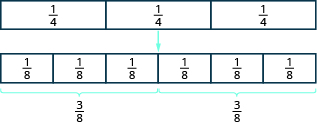
Figure \(\PageIndex{1}\)
We see \(\dfrac{6}{8}\) is equivalent to \(\dfrac{3}{4}\). Taking half of the six \(\dfrac{1}{8}\) tiles gives us three \(\dfrac{1}{8}\) tiles, which is \(\dfrac{3}{8}\). Therefore,
\[\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8} \nonumber \]
Use a diagram to model \(\dfrac{1}{2} \cdot \dfrac{3}{4}\).
Solution
First shade in \(\dfrac{3}{4}\) of the rectangle.

We will take \(\dfrac{1}{2}\) of this \(\dfrac{3}{4}\), so we heavily shade \(\dfrac{1}{2}\) of the shaded region.
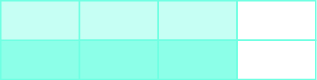
Notice that 3 out of the 8 pieces are heavily shaded. This means that \(\dfrac{3}{8}\) of the rectangle is heavily shaded. Therefore, \(\dfrac{1}{2}\) of \(\dfrac{3}{4}\) is \(\dfrac{3}{4}\), or \(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\).
Use a diagram to model: \(\dfrac{1}{2} \cdot \dfrac{3}{5}\).
- Answer
-
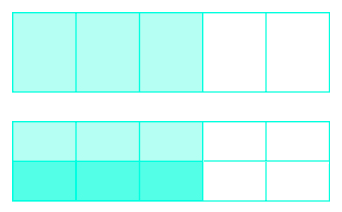
\(\dfrac{3}{10}\)
Use a diagram to model: \(\dfrac{1}{2} \cdot \dfrac{5}{6}\).
- Answer
-
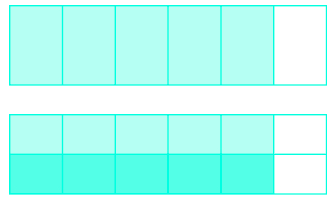
\(\dfrac{5}{12}\)
Look at the result we got from the model in Example \(\PageIndex{6}\). We found that \(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\). Do you notice that we could have gotten the same answer by multiplying the numerators and multiplying the denominators?
| \(\dfrac{1}{2} \cdot \dfrac{3}{4}\) | |
| Multiply the numerators, and multiply the denominators. | \(\dfrac{1}{2} \cdot \dfrac{3}{4}\) |
| Simplify. | \(\dfrac{3}{8}\) |
This leads to the definition of fraction multiplication. To multiply fractions, we multiply the numerators and multiply the denominators. Then we write the fraction in simplified form.
If \(a, b, c,\) and \(d\) are numbers where \(b ≠ 0\) and \(d ≠ 0\), then
\[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]
Multiply, and write the answer in simplified form: \(\dfrac{3}{4} \cdot \dfrac{1}{5}\).
Solution
| \(\dfrac{3}{4} \cdot \dfrac{1}{5}\) | |
| Multiply the numerators, and multiply the denominators. | \(\dfrac{3 \cdot 1}{4 \cdot 5}\) |
| Simplify. | \(\dfrac{3}{20}\) |
There are no common factors, so the fraction is simplified.
Multiply, and write the answer in simplified form: \(\dfrac{1}{3} \cdot \dfrac{2}{5}\).
- Answer
-
\(\dfrac{2}{15}\)
Multiply, and write the answer in simplified form: \(\dfrac{3}{5} \cdot \dfrac{7}{8}\).
- Answer
-
\(\dfrac{21}{40}\)
When multiplying fractions, the properties of positive and negative numbers still apply. It is a good idea to determine the sign of the product as the first step. In Example \(\PageIndex{8}\) we will multiply two negatives, so the product will be positive.
Multiply, and write the answer in simplified form: \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\).
Solution
| \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\) | |
| The signs are the same, so the product is positive. Multiply the numerators, multiply the denominators. | \(\dfrac{5 \cdot 2}{8 \cdot 3}\) |
| Simplify. | \(\dfrac{10}{24}\) |
| Look for common factors in the numerator and denominator. Rewrite showing common factors. | \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\) |
| Remove common factors. | \(\dfrac{5}{12}\) |
Another way to find this product involves removing common factors earlier.
| \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\) | |
| Determine the sign of the product. Multiply. | \(\dfrac{5 \cdot 2}{8 \cdot 3}\) |
| Show common factors and then remove them. | \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\) |
| Multiply remaining factors. | \(\dfrac{5}{12}\) |
We get the same result.
Multiply, and write the answer in simplified form: \(- \dfrac{4}{7} \left(- \dfrac{5}{8}\right)\).
- Answer
-
\(\dfrac{5}{14}\)
Multiply, and write the answer in simplified form: \(- \dfrac{7}{12} \left(- \dfrac{8}{9}\right)\).
- Answer
-
\(\dfrac{14}{27}\)
Multiply, and write the answer in simplified form: \(− \dfrac{14}{15} \cdot \dfrac{20}{21}\).
Solution
| \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\) | |
| Determine the sign of the product; multiply. | \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\) |
| Are there any common factors in the numerator and the denominator? We know that 7 is a factor of 14 and 21, and 5 is a factor of 20 and 15. | |
| Rewrite showing common factors. | \(- \dfrac{2 \cdot \cancel{\textcolor{red}{7}} \cdot 4 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}} \cdot 3 \cdot \cancel{\textcolor{red}{7}}}\) |
| Remove the common factors. | \(- \dfrac{2 \cdot 4}{3 \cdot 3}\) |
| Multiply the remaining factors. | \(- \dfrac{8}{9}\) |
Multiply, and write the answer in simplified form: \(− \dfrac{10}{28} \cdot \dfrac{8}{15}\).
- Answer
-
\(-\dfrac{4}{21}\)
Multiply, and write the answer in simplified form: \(− \dfrac{9}{20} \cdot \dfrac{5}{12}\).
- Answer
-
\(-\dfrac{3}{16}\)
When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, a, can be written as \(\dfrac{a}{1}\). So, \(3 = \dfrac{3}{1}\), for example.
Multiply, and write the answer in simplified form:
- \(\dfrac{1}{7} \cdot 56\)
- \(\dfrac{12}{5} (−20x)\)
Solution
| \(\dfrac{1}{7} \cdot 56\) | |
| Write 56 as a fraction. | \(\dfrac{1}{7} \cdot \dfrac{56}{1}\) |
| Determine the sign of the product; multiply. | \(\dfrac{56}{7}\) |
| Simplify. | \(8\) |
| \(\dfrac{12}{5} (-20x)\) | |
| Write −20x as a fraction. | \(\dfrac{12}{5} \left(\dfrac{-20x}{1}\right)\) |
| Determine the sign of the product; multiply. | \(- \dfrac{12 \cdot 20 \cdot x}{5 \cdot 1}\) |
| Show common factors and then remove them. | \(- \dfrac{12 \cdot \textcolor{red}{4 \cdot \cancel{5} x}}{\cancel{5} \cdot 1}\) |
| Multiply remaining factors; simplify. | \(-48x\) |
Multiply, and write the answer in simplified form:
- \(\dfrac{1}{8} • 72\)
- \(\dfrac{11}{3} (−9a)\)
- Answer a
-
\(9\)
- Answer b
-
\(-33a\)
Multiply, and write the answer in simplified form:
- \(\dfrac{3}{8} • 64\)
- \(16x • \dfrac{11}{12}\)
- Answer a
-
\(24\)
- Answer b
-
\(\dfrac{44x}{3}\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


