4.7: Add and Subtract Fractions with Common Denominators
- Page ID
- 4994
- Model fraction addition
- Add fractions with a common denominator
- Model fraction subtraction
- Subtract fractions with a common denominator
Before you get started, take this readiness quiz.
- Simplify: \(2x + 9 + 3x − 4\). If you missed this problem, review Example 2.2.10.
- Draw a model of the fraction \(\dfrac{3}{4}\). If you missed this problem, review Example 4.1.2.
- Simplify: \(\dfrac{3 + 2}{6}\). If you missed this problem, review Example 4.3.12.
Model Fraction Addition
How many quarters are pictured? One quarter plus \(2\) quarters equals \(3\) quarters.

Figure \(\PageIndex{1}\)
Remember, quarters are really fractions of a dollar. Quarters are another way to say fourths. So the picture of the coins shows that
\[\begin{split} \dfrac{1}{4} \qquad \qquad \qquad \dfrac{2}{4} \qquad & \qquad \qquad \dfrac{3}{4} \\ one \; quarter + two \; quarters &= three\; quarters \end{split} \nonumber \]
Let’s use fraction circles to model the same example, \(\dfrac{1}{4} + \dfrac{2}{4}\).
| Start with one \(\dfrac{1}{4}\) piece. |  |
\(\dfrac{1}{4}\) |
| Add two more \(\dfrac{1}{4}\) pieces. | 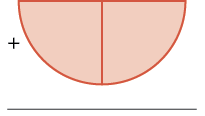 |
\(+ \dfrac{2}{4}\) |
| The result is \(\dfrac{3}{4}\). | 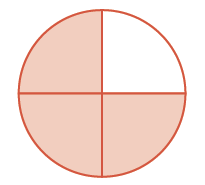 |
\(\dfrac{3}{4}\) |
So again, we see that
\[\dfrac{1}{4} + \dfrac{2}{4} = \dfrac{3}{4} \nonumber \]
Use a model to find the sum \(\dfrac{3}{8} + \dfrac{2}{8}\).
Solution
| Start with three \(\dfrac{1}{8}\) pieces. | 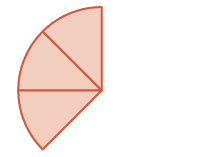 |
\(\dfrac{3}{8}\) |
| Add two \(\dfrac{1}{8}\) pieces. | 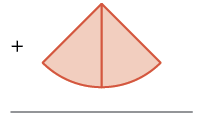 |
\(+ \dfrac{2}{8}\) |
| How many \(\dfrac{1}{8}\) pieces are there? | 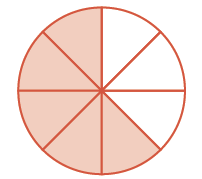 |
\(\dfrac{5}{8}\) |
There are five \(\dfrac{1}{8}\) pieces, or five-eighths. The model shows that \(\dfrac{3}{8} + \dfrac{2}{8} = \dfrac{5}{8}\).
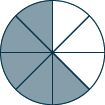
Use a model to find each sum. Show a diagram to illustrate your model. \[\dfrac{1}{8} + \dfrac{4}{8} \nonumber \]
- Answer
-
\(\dfrac{5}{8}\)
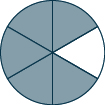
Use a model to find each sum. Show a diagram to illustrate your model. \[\dfrac{1}{6} + \dfrac{4}{6} \nonumber \]
- Answer
-
\(\dfrac{5}{6}\)
Add Fractions with a Common Denominator
Example \(\PageIndex{1}\) shows that to add the same-size pieces—meaning that the fractions have the same denominator—we just add the number of pieces.
If \(a\), \(b\), and \(c\) are numbers where \(c ≠ 0\), then
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\]
To add fractions with a common denominator, add the numerators and place the sum over the common denominator.
Find the sum: \(\dfrac{3}{5} + \dfrac{1}{5}\).
Solution
| Add the numerators and place the sum over the common denominator. | \(\dfrac{3 + 1}{5}\) |
| Simplify. | \(\dfrac{4}{5}\) |
Find each sum: \(\dfrac{3}{6} + \dfrac{2}{6}\).
- Answer
-
\(\dfrac{5}{6}\)
Find each sum: \(\dfrac{3}{10} + \dfrac{7}{10}\).
- Answer
-
\(1\)
Find the sum: \(\dfrac{x}{3} + \dfrac{2}{3}\).
Solution
| Add the numerators and place the sum over the common denominator. | \(\dfrac{x + 2}{3}\) |
Note that we cannot simplify this fraction any more. Since \(x\) and \(2\) are not like terms, we cannot combine them.
Find the sum: \(\dfrac{x}{4} + \dfrac{3}{4}\).
- Answer
-
\(\dfrac{x+3}{4}\)
Find the sum: \(\dfrac{y}{8} + \dfrac{5}{8}\).
- Answer
-
\(\dfrac{y+5}{8}\)
Find the sum: \(− \dfrac{9}{d} + \dfrac{3}{d}\).
Solution
We will begin by rewriting the first fraction with the negative sign in the numerator.
\[− \dfrac{a}{b} = \dfrac{−a}{b} \nonumber \]
| Rewrite the first fraction with the negative in the numerator. | \(\dfrac{-9}{d} + \dfrac{3}{d}\) |
| Add the numerators and place the sum over the common denominator. | \(\dfrac{-9 + 3}{d}\) |
| Simplify the numerator. | \(\dfrac{-6}{d}\) |
| Rewrite with negative sign in front of the fraction. | \(- \dfrac{6}{d}\) |
Find the sum: \(− \dfrac{7}{d} + \dfrac{8}{d}\).
- Answer
-
\(\dfrac{1}{d}\)
Find the sum: \(− \dfrac{6}{m} + \dfrac{9}{m}\).
- Answer
-
\(\dfrac{3}{m}\)
Find the sum: \(\dfrac{2n}{11} + \dfrac{5n}{11}\).
Solution
| Add the numerators and place the sum over the common denominator. | \(\dfrac{2n + 5n}{11}\) |
| Combine like terms. | \(\dfrac{7n}{11}\) |
Find the sum: \(\dfrac{3p}{8} + \dfrac{6p}{8}\).
- Answer
-
\(\dfrac{9p}{8}\)
Find the sum: \(\dfrac{2q}{5} + \dfrac{7q}{5}\).
- Answer
-
\(\dfrac{9q}{5}\)
Find the sum: \(− \dfrac{3}{12} + \left(− \dfrac{5}{12}\right)\).
Solution
| Add the numerators and place the sum over the common denominator. | \(\dfrac{-3 + (-5)}{12}\) |
| Add. | \(\dfrac{-8}{12}\) |
| Simplify the fraction. | \(-\dfrac{2}{3}\) |
Find each sum: \(− \dfrac{4}{15} + \left(− \dfrac{6}{15}\right)\).
- Answer
-
\(-\dfrac{2}{3}\)
Find each sum: \(− \dfrac{5}{21} + \left(− \dfrac{9}{21}\right)\).
- Answer
-
\(-\dfrac{2}{3}\)
Model Fraction Subtraction
Subtracting two fractions with common denominators is much like adding fractions. Think of a pizza that was cut into \(12\) slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or \(\dfrac{7}{12}\) of the pizza) left in the box. If Leonardo eats \(2\) of these remaining pieces (or \(\dfrac{2}{12}\) of the pizza), how much is left? There would be \(5\) pieces left (or \(\dfrac{5}{12}\) of the pizza).
\[\dfrac{7}{12} - \dfrac{2}{12} = \dfrac{5}{12} \nonumber \]
Let’s use fraction circles to model the same example, \(\dfrac{7}{12} − \dfrac{2}{12}\). Start with seven \(\dfrac{1}{12}\) pieces. Take away two \(\dfrac{1}{12}\) pieces. How many twelfths are left?
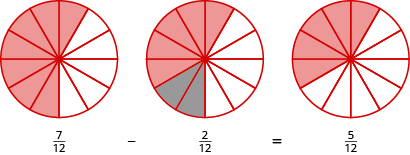
Figure \(\PageIndex{2}\)
Again, we have five twelfths, \(\dfrac{5}{12}\).
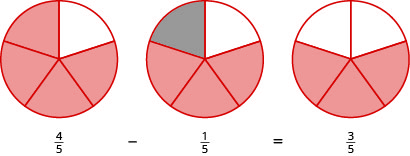
Use fraction circles to find the difference: \(\dfrac{4}{5} − \dfrac{1}{5}\).
Solution
Start with four \(\dfrac{1}{5}\) pieces. Take away one \(\dfrac{1}{5}\) piece. Count how many fifths are left. There are three \(\dfrac{1}{5}\) pieces left.
Use a model to find each difference. Show a diagram to illustrate your model. \(\dfrac{7}{8} − \dfrac{4}{8}\)
- Answer
-
\(\dfrac{3}{8}\), models may differ.
Use a model to find each difference. Show a diagram to illustrate your model. \(\dfrac{5}{6} − \dfrac{4}{6}\)
- Answer
-
\(\dfrac{1}{6}\), models may differ.
Subtract Fractions with a Common Denominator
We subtract fractions with a common denominator in much the same way as we add fractions with a common denominator.
If \(a\), \(b\), and \(c\) are numbers where \(c ≠ 0\), then
\[\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\]
To subtract fractions with a common denominator, we subtract the numerators and place the difference over the common denominator.
Find the difference: \(\dfrac{23}{24} − \dfrac{14}{24}\).
Solution
| Subtract the numerators and place the difference over the common denominator. | \(\dfrac{23 - 14}{24}\) |
| Simplify the numerator. | \(\dfrac{9}{24}\) |
| Simplify the fraction by removing common factors. | \(\dfrac{3}{8}\) |
Find the difference: \(\dfrac{19}{28} − \dfrac{7}{28}\).
- Answer
-
\(\dfrac{3}{7}\)
Find the difference: \(\dfrac{27}{32} − \dfrac{11}{32}\).
- Answer
-
\(\dfrac{1}{2}\)
Find the difference: \(\dfrac{y}{6} − \dfrac{1}{6}\).
Solution
| Subtract the numerators and place the difference over the common denominator. | \(\dfrac{y - 1}{6}\) |
The fraction is simplified because we cannot combine the terms in the numerator.
Find the difference: \(\dfrac{x}{7} − \dfrac{2}{7}\).
- Answer
-
\(\dfrac{x-2}{7}\)
Find the difference: \(\dfrac{y}{14} − \dfrac{13}{14}\).
- Answer
-
\(\dfrac{y-13}{14}\)
Find the difference: \(− \dfrac{10}{x} − \dfrac{4}{x}\).
Solution
Remember, the fraction \(− \dfrac{10}{x}\) can be written as \(\dfrac{−10}{x}\).
| Subtract the numerators. | \(\dfrac{-10 - 4}{x}\) |
| Simplify. | \(\dfrac{-14}{x}\) |
| Rewrite with the negative sign in front of the fraction. | \(- \dfrac{14}{x}\) |
Find the difference: \(− \dfrac{9}{x} − \dfrac{7}{x}\).
- Answer
-
\(-\dfrac{16}{x}\)
Find the difference: \(− \dfrac{17}{a} − \dfrac{5}{a}\).
- Answer
-
\(-\dfrac{22}{a}\)
Now lets do an example that involves both addition and subtraction.
Simplify: \(\dfrac{3}{8} + \left(- \dfrac{5}{8}\right) − \dfrac{1}{8}\).
Solution
| Combine the numerators over the common denominator. | \(\dfrac{3 + (-5) - 1}{8}\) |
| Simplify the numerator, working left to right. | \(\dfrac{-2 - 1}{8}\) |
| Subtract the terms in the numerator. | \(\dfrac{-3}{8}\) |
| Rewrite with the negative sign in front of the fraction. | \(- \dfrac{3}{8}\) |
Simplify: \(\dfrac{2}{5} + \left(− \dfrac{4}{5}\right) − \dfrac{3}{5}\).
- Answer
-
\(-1\)
Simplify: \(\dfrac{5}{9} + \left(− \dfrac{4}{9}\right) − \dfrac{7}{9}\).
- Answer
-
\(-\dfrac{2}{3}\)
Access Additional Online Resources
- Adding Fractions With Pattern Blocks
- Adding Fractions With Like Denominators
- Subtracting Fractions With Like Denominators
Key Concepts
- Fraction Addition
- If \(a,b,\) and \(c\) are numbers where \(c\neq 0\), then \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
- To add fractions, add the numerators and place the sum over the common denominator.
- Fraction Subtraction
- If \(a,b,\) and \(c\) are numbers where \(c\neq 0\), then \(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
- To subtract fractions, subtract the numerators and place the difference over the common denominator.
Practice Makes Perfect
Model Fraction Addition
In the following exercises, use a model to add the fractions. Show a diagram to illustrate your model.
- \(\dfrac{2}{5} + \dfrac{1}{5}\)
- \(\dfrac{3}{10} + \dfrac{4}{10}\)
- \(\dfrac{1}{6} + \dfrac{3}{6}\)
- \(\dfrac{3}{8} + \dfrac{3}{8}\)
Add Fractions with a Common Denominator
In the following exercises, find each sum.
- \(\dfrac{4}{9} + \dfrac{1}{9}\)
- \(\dfrac{2}{9} + \dfrac{5}{9}\)
- \(\dfrac{6}{13} + \dfrac{7}{13}\)
- \(\dfrac{9}{15} + \dfrac{7}{15}\)
- \(\dfrac{x}{4} + \dfrac{3}{4}\)
- \(\dfrac{y}{3} + \dfrac{2}{3}\)
- \(\dfrac{7}{p} + \dfrac{9}{p}\)
- \(\dfrac{8}{q} + \dfrac{6}{q}\)
- \(\dfrac{8b}{9} + \dfrac{3b}{9}\)
- \(\dfrac{5a}{7} + \dfrac{4a}{7}\)
- \(\dfrac{-12y}{8} + \dfrac{3y}{8}\)
- \(\dfrac{-11x}{5} + \dfrac{7x}{5}\)
- \(− \dfrac{1}{8} + \left(− \dfrac{3}{8}\right)\)
- \(− \dfrac{1}{8} + \left(− \dfrac{5}{8}\right)\)
- \(− \dfrac{3}{16} + \left(− \dfrac{7}{16}\right)\)
- \(− \dfrac{5}{16} + \left(− \dfrac{9}{16}\right)\)
- \(− \dfrac{8}{17} + \dfrac{15}{17}\)
- \(− \dfrac{9}{19} + \dfrac{17}{19}\)
- \(− \dfrac{6}{13} + \left(− \dfrac{10}{13}\right) + \left(- \dfrac{12}{13}\right)\)
- \(− \dfrac{5}{12} + \left(− \dfrac{7}{12}\right) + \left(- \dfrac{11}{12}\right)\)
Model Fraction Subtraction
In the following exercises, use a model to subtract the fractions. Show a diagram to illustrate your model.
- \(\dfrac{5}{8} − \dfrac{2}{8}\)
- \(\dfrac{5}{6} − \dfrac{2}{6}\)
Subtract Fractions with a Common Denominator
In the following exercises, find the difference.
- \(\dfrac{4}{5} − \dfrac{1}{5}\)
- \(\dfrac{4}{5} − \dfrac{3}{5}\)
- \(\dfrac{11}{15} − \dfrac{7}{15}\)
- \(\dfrac{9}{13} − \dfrac{4}{13}\)
- \(\dfrac{11}{12} − \dfrac{5}{12}\)
- \(\dfrac{7}{12} − \dfrac{5}{12}\)
- \(\dfrac{4}{21} − \dfrac{19}{21}\)
- \(- \dfrac{8}{9} − \dfrac{16}{9}\)
- \(\dfrac{y}{17} − \dfrac{9}{17}\)
- \(\dfrac{x}{19} − \dfrac{8}{19}\)
- \(\dfrac{5y}{8} − \dfrac{7}{8}\)
- \(\dfrac{11z}{13} − \dfrac{8}{13}\)
- \(- \dfrac{8}{d} − \dfrac{3}{d}\)
- \(- \dfrac{7}{c} − \dfrac{7}{c}\)
- \(- \dfrac{23}{u} − \dfrac{15}{u}\)
- \(- \dfrac{29}{v} − \dfrac{26}{v}\)
- \(- \dfrac{6c}{7} − \dfrac{5c}{7}\)
- \(- \dfrac{12d}{11} − \dfrac{9d}{11}\)
- \(\dfrac{-4r}{13} − \dfrac{5r}{13}\)
- \(\dfrac{-7s}{3} − \dfrac{7s}{3}\)
- \(- \dfrac{3}{5} − \left(- \dfrac{4}{5}\right)\)
- \(- \dfrac{3}{7} − \left(- \dfrac{5}{7}\right)\)
- \(- \dfrac{7}{9} − \left(- \dfrac{5}{9}\right)\)
- \(- \dfrac{8}{11} − \left(- \dfrac{5}{11}\right)\)
Mixed Practice
In the following exercises, perform the indicated operation and write your answers in simplified form.
- \(− \dfrac{5}{18} \cdot \dfrac{9}{10}\)
- \(− \dfrac{3}{14} \cdot \dfrac{7}{12}\)
- \(\dfrac{n}{5} − \dfrac{4}{5}\)
- \(\dfrac{6}{11} − \dfrac{s}{11}\)
- \(- \dfrac{7}{24} − \dfrac{2}{24}\)
- \(- \dfrac{5}{18} − \dfrac{1}{18}\)
- \(\dfrac{8}{15} \div \dfrac{12}{5}\)
- \(\dfrac{7}{12} \div \dfrac{9}{28}\)
Everyday Math
- Trail Mix Jacob is mixing together nuts and raisins to make trail mix. He has \(\dfrac{6}{10}\) of a pound of nuts and \(\dfrac{3}{10}\) of a pound of raisins. How much trail mix can he make?
- Baking Janet needs \(\dfrac{5}{8}\) of a cup of flour for a recipe she is making. She only has \(\dfrac{3}{8}\) of a cup of flour and will ask to borrow the rest from her next-door neighbor. How much flour does she have to borrow?
Writing Exercises
- Greg dropped his case of drill bits and three of the bits fell out. The case has slots for the drill bits, and the slots are arranged in order from smallest to largest. Greg needs to put the bits that fell out back in the case in the empty slots. Where do the three bits go? Explain how you know.
Bits in case: \(\dfrac{1}{16}, \dfrac{1}{8}\), ___, ___, \(\dfrac{5}{16}, \dfrac{3}{8}\), ___, \(\dfrac{1}{2}, \dfrac{9}{16}, \dfrac{5}{8}\).
Bits that fell out: \(\dfrac{7}{16}, \dfrac{3}{16}, \dfrac{1}{4}\).
- After a party, Lupe has \(\dfrac{5}{12}\) of a cheese pizza, \(\dfrac{4}{12}\) of a pepperoni pizza, and \(\dfrac{4}{12}\) of a veggie pizza left. Will all the slices fit into 1 pizza box? Explain your reasoning.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


