7.3: Some Properties of Integrals
- Page ID
- 508
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose an object moves so that its speed, or more properly velocity, is given by \(v(t)=-t^2+5t\), as shown in figure 7.3.1. Let's examine the motion of this object carefully. We know that the velocity is the derivative of position, so position is given by \(s(t)=-t^3/3+5t^2/2+C\). Let's suppose that at time \(t=0\) the object is at position 0, so \(s(t)=-t^3/3+5t^2/2\); this function is also pictured in figure 7.3.1.
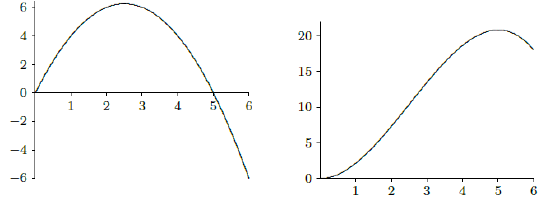
Between \(t=0\) and \(t=5\) the velocity is positive, so the object moves away from the starting point, until it is a bit past position 20. Then the velocity becomes negative and the object moves back toward its starting point. The position of the object at \(t=5\) is exactly \(s(5)=125/6\), and at \(t=6\) it is \(s(6)=18\). The total distance traveled by the object is therefore \(125/6 + (125/6 - 18) = 71/3\approx 23.7\).
As we have seen, we can also compute distance traveled with an integral; let's try it.
\[ \int_0^6 v(t)\,dt = \int_0^6 -t^2+5t\,dt = \left.{-t^3\over 3}+{5\over2}t^2\right|_0^6 = 18. \nonumber \]
What went wrong? Well, nothing really, except that it's not really true after all that "we can also compute distance traveled with an integral''. Instead, as you might guess from this example, the integral actually computes the net distance traveled, that is, the difference between the starting and ending point.
As we have already seen,
\[ \int_0^6 v(t)\,dt=\int_0^5 v(t)\,dt+\int_5^6 v(t)\,dt. \nonumber \]
Computing the two integrals on the right (do it!) gives \(125/6\) and \(-17/6\), and the sum of these is indeed 18. But what does that negative sign mean? It means precisely what you might think: it means that the object moves backwards. To get the total distance traveled we can add \(125/6+17/6=71/3\), the same answer we got before.
Remember that we can also interpret an integral as measuring an area, but now we see that this too is a little more complicated that we have suspected. The area under the curve \(v(t)\) from 0 to 5 is given by
\[ \int_0^5 v(t)\,dt={125\over6}, \nonumber \]
and the "area'' from 5 to 6 is
\[ \int_5^6 v(t)\,dt=-{17\over 6}. \nonumber \]
In other words, the area between the \(x\)-axis and the curve, but under the \(x\)-axis, "counts as negative area''. So the integral \[ \int_0^6 v(t)\,dt=18 \nonumber \] measures "net area'', the area above the axis minus the (positive) area below the axis.
If we recall that the integral is the limit of a certain kind of sum, this behavior is not surprising. Recall the sort of sum involved: \[ \sum_{i=0}^{n-1} v(t_i)\Delta t. \nonumber \] In each term \(v(t)\Delta t\) the \(\Delta t\) is positive, but if \(v(t_i)\) is negative then the term is negative. If over an entire interval, like 5 to 6, the function is always negative, then the entire sum is negative. In terms of area, \(v(t)\Delta t\) is then a negative height times a positive width, giving a negative rectangle "area''.
So now we see that when evaluating \( \int_5^6 v(t)\,dt=-{17\over 6}\) by finding an antiderivative, substituting, and subtracting, we get a surprising answer, but one that turns out to make sense.
Let's now try something a bit different:
\[ \int_6^5 v(t)\,dt=\left.{-t^3\over 3}+{5\over2}t^2\right|_6^5 = {-5^3\over 3}+{5\over2}5^2-{-6^3\over 3}-{5\over2}6^2 ={17\over 6}. \nonumber \]
Here we simply interchanged the limits 5 and 6, so of course when we substitute and subtract we're subtracting in the opposite order and we end up multiplying the answer by \(-1\). This too makes sense in terms of the underlying sum, though it takes a bit more thought. Recall that in the sum \[ \sum_{i=0}^{n-1} v(t_i)\Delta t, \nonumber \] the \(\Delta t\) is the "length'' of each little subinterval, but more precisely we could say that \(\Delta t = t_{i+1}-t_i\), the difference between two endpoints of a subinterval. We have until now assumed that we were working left to right, but could as well number the subintervals from right to left, so that \(t_0=b\) and \(t_n=a\). Then (\Delta t=t_{i+1}-t_i\) is negative and in
\[ \int_6^5 v(t)\,dt=\sum_{i=0}^{n-1} v(t_i)\Delta t, \nonumber \]
the values \(v(t_i)\) are negative but also \(\Delta t\) is negative, so all terms are positive again. On the other hand, in
\[ \int_5^0 v(t)\,dt=\sum_{i=0}^{n-1} v(t_i)\Delta t, \nonumber \]
the values \(v(t_i)\) are positive, but \(\Delta t\) is negative,and we get a negative result:
\[ \int_5^0 v(t)\,dt=\left.{-t^3\over 3}+{5\over2}t^2\right|_5^0 = 0-{-5^3\over 3}-{5\over2}5^2 = -{125\over6}. \nonumber \]
Finally we note one simple property of integrals:
\[ \int_a^b f(x)+g(x)\,dx=\int_a^b f(x)\,dx+\int_a^b g(x)\,dx. \nonumber \]
This is easy to understand once you recall that \((F(x)+G(x))'=F'(x)+G'(x)\). Hence, if \(F'(x)=f(x)\) and \(G'(x)=g(x)\), then
\[ \eqalign{ \int_a^b f(x)+g(x)\,dx&=\left.(F(x)+G(x))\right|_a^b\cr &=F(b)+G(b)-F(a)-G(a)\cr &=F(b)-F(a)+G(b)-G(a)\cr &=\left.F(x)\right|_a^b+\left.G(x)\right|_a^b\cr &=\int_a^b f(x)\,dx+\int_a^b g(x)\,dx.\cr } \nonumber \]
In summary, we will frequently use these properties of integrals:
\[\displaylines{ \int_a^b f(x)\,dx = \int_a^c f(x)\,dx + \int_c^b f(x)\,dx\cr \int_a^b f(x)+g(x)\,dx=\int_a^b f(x)\,dx+\int_a^b g(x)\,dx\cr \int_a^b f(x)\,dx=-\int_b^a f(x)\,dx\cr } \nonumber \]
and if \(a < b\) and \(f(x)\le 0\) on \([a,b]\) then
\[ \int_a^b f(x)\,dx\le 0 \nonumber \]
and in fact
\[ \int_a^b f(x)\,dx=-\int_a^b |f(x)|\,dx. \nonumber \]


