Parameterizing a Piecewise Path
- Last updated
- Dec 21, 2020
- Save as PDF
- Page ID
- 10922
( \newcommand{\kernel}{\mathrm{null}\,}\)
There are times when it is necessary to parameterize a path made up of pieces of different curves. This piecewise path may be open or form the boundary of a closed region as does the example shown in Figure 4. In addition to determining a vector-valued function to trace out each piece separately, with the indicated orientation, we also need to determine a suitable range of values for the parameter t.
Note that there are many ways to parameterize any one piece, so there are many correct ways to parameterize a path in this way.
Example 6: Parameterizing a piecewise path
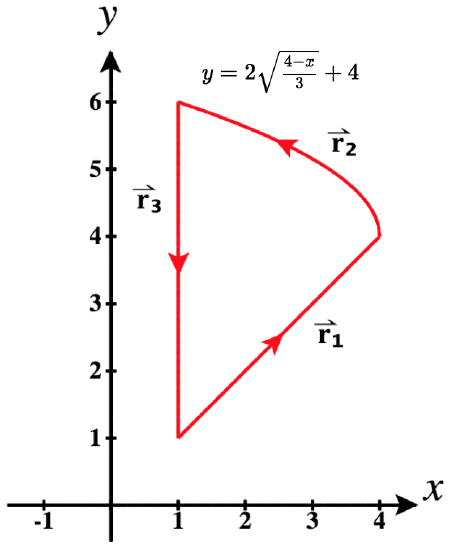 Determine a piecewise parameterization of the path shown in Figure 4, starting with t=0 and continuing on through each piece.
Determine a piecewise parameterization of the path shown in Figure 4, starting with t=0 and continuing on through each piece.
Solution
Our first task is to identify the three pieces in this piecewise path.
Note how we labeled these sequentially as ⇀r1, ⇀r2, and ⇀r3. Now we need to identify the function for each and write the corresponding vector-valued function with the correct orientation (left-to-right or right-to-left).
Determining ⇀r1: The equation of the linear function in this piece is y=x.
Since it is oriented from left-to-right between t=1 and t=4, we can write:
⇀r1a(t)=tˆi+tˆjfor1≤t≤4
If we wish to begin this piece at t=0, we just need to shift the value of t one unit to the left. One way to do this is to write ⇀r1a in terms of t1 instead of t to make the translation easier to see.
Thus, we have ⇀r1a(t1)=t1ˆi+t1ˆj for 1≤t1≤4.
Figure 4: A closed piecewise path
Subtracting 1 from each part of this range of parameter values, we have: 0≤t1−1≤3.
Now we let t=t1−1. Solving for t1, we obtain: t1=t+1.
Replacing t1 with the expression t+1 will effectively shift the range of parameter values one unit to the left.
So, starting with t=0, we have: ⇀r1(t)=(t+1)ˆi+(t+1)ˆjfor0≤t≤3
Double-check that this vector-valued function will trace out this segment in the correct direction before going on to r2.
Determining ⇀r2: This piece has a label showing the function whose graph it traces along. If it were oriented from left-to-right, we would have:
Left-to-right:⇀r2a(t)=tˆi+(2√4−t3+4)ˆjfor1≤t≤4
But since we need it to be oriented from right-to-left, we need to replace t with −t in the function and we need to divide through the range inequality by -1 to obtain the corresponding range. Thus we obtain:
⇀r2b(t)=−tˆi+(2√4−(−t)3+4)ˆjfor−4≤t≤−1
Check that it works!
Now we wish to have this piece start at t=3 just after the first one finishes. Again let's make this easier to see by writing r2b in terms on t2.
⇀r2b(t2)=−t2ˆi+(2√4−(−t2)3+4)ˆjfor−4≤t2≤−1
To force r2 to start with t=3 instead of t=−4, we need to add 7 to each part of the inequality. This yields: 3≤t2+7≤6.
Let t=t2+7. Then solving for −t2 (since this is what we need to replace in r2b), we have: −t2=7−t.
Replacing −t2 with (7−t) in ⇀r2b, we obtain:
⇀r2(t)=(7−t)ˆi+(2√4−(7−t)3+4)ˆjfor3≤t≤6
This can be combined with our earlier result for r1 to write a piecewise-defined vector-valued function that traces out the first two pieces, starting at t=0:
⇀r(t)={(t+1)ˆi+(t+1)ˆj,0≤t≤3(7−t)ˆi+(2√t−33+4)ˆj,3<t≤6
Note that one small modification was made to the second range so that when t=3, there is no confusion about which piece to evaluate.
Determining ⇀r3: To determine this last piece we need to think a little differently. This is because it is a vertical segment, which cannot be represented with a function of the form, y=f(x). Note that it could be represented by a function of the form x=f(y). Letting y=t, we can write x=f(t) and writing a parameterization in increasing y values (bottom-to-top), we'd get: ⇀r(t)=f(t)ˆi+tˆj.
The equation of this line is x=1. Thus, if we wished to parameterize this segment with upward orientation (increasing values of y), we have:
⇀r3a(t)=1ˆi+tˆjfor1≤t≤6
But since we wish to use a downward orientation (decreasing values of y), we need to use a decreasing function of t for y. As before, the simplest case is to use y=−t. Then, in the general case, we'd trace a function x=f(y) in a downwards orientation with ⇀r(t)=f(−t)ˆi−tˆj.
In the case of r3, this gives us:
⇀r3b(t)=1ˆi−tˆjfor−6≤t≤−1
Note that since x=1,f(−t)=1, that is, it did not change the first component since it was constant and not a variable function of the parameter t.
Also note that since we negated t, we also had to negate the range, dividing it through by −1.
As above, to facilitate the translation, we'll replace t with t3, giving us:
⇀r3b(t3)=1ˆi−t3ˆjfor−6≤t3≤−1
Now, we wish this final piece to start at t=6 where the second piece we formed above leaves off. We see that we need to add 12 to the range of paramater t to accomplish this, giving us a new range of 6≤t3+12≤11.
Let t=t3+12. Then solving for −t3 (since this is what we need to replace in r3b), we have: −t3=12−t.
Replacing −t3 with (12−t) in ⇀r3b, we obtain:
⇀r3(t)=1ˆi+(12−t)ˆjfor6≤t≤11
Check that this still traces out this vertical segment from top-to-bottom.
We can now state the final answer as a single piecewise-defined vector-valued function that traces out this entire path, starting when t=0.
⇀r(t)={(t+1)ˆi+(t+1)ˆj,0≤t≤3(7−t)ˆi+(2√t−33+4)ˆj,3<t≤61ˆi+(12−t)ˆj6<t≤11
Be sure to verify that this single vector-valued function does indeed trace out the entire path!
Exercises:
For questions 41 - 44, provide a parameterization for each piecewise path. Try to write a parameterization that starts with t=0 and progresses on through values of t as you move from one piece to another.
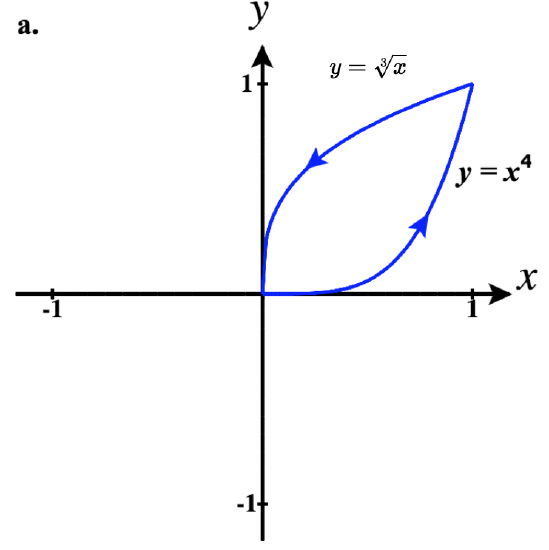
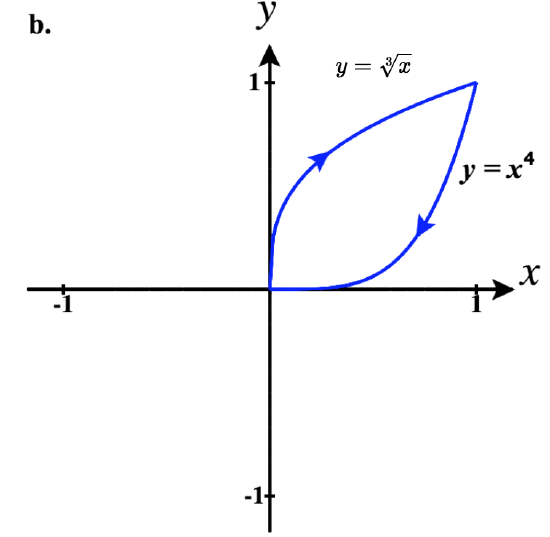
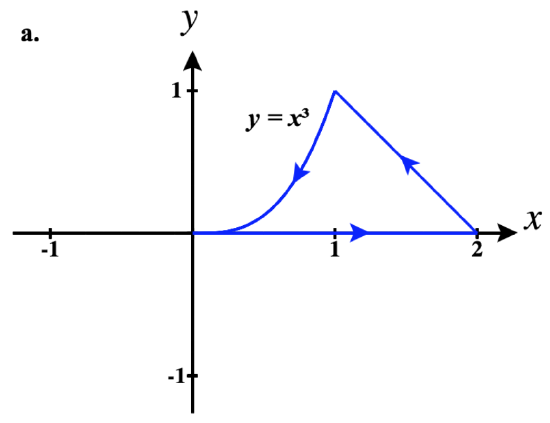
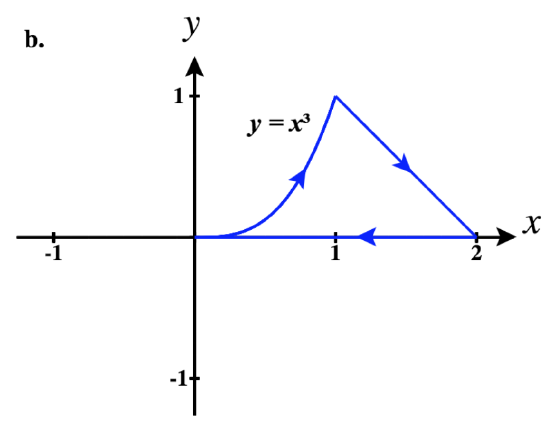
41)
- Answer
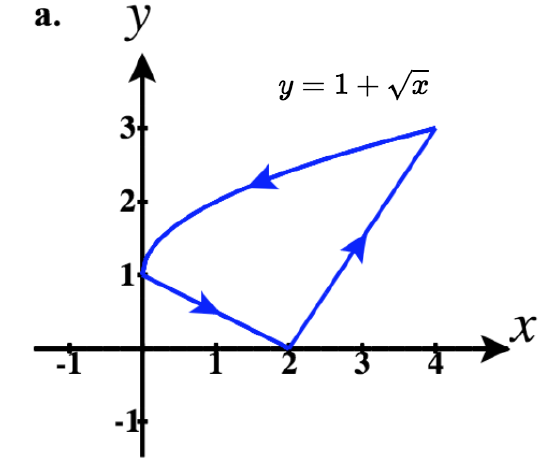
- a. ⇀r1(t)=tˆi+t4ˆj for 0≤t≤1
⇀r2(t)=−tˆi+3√−tˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+t4ˆj,0≤t≤1(2−t)ˆi+3√2−tˆj,1<t≤2
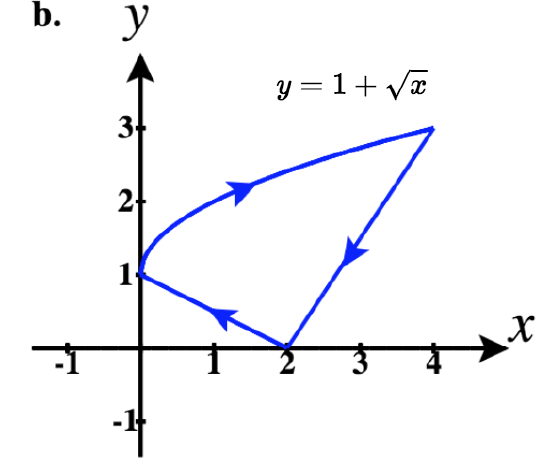
b. ⇀r1(t)=tˆi+3√tˆj for 0≤t≤1
⇀r2(t)=−tˆi+(−t)4ˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+3√tˆj,0≤t≤1(2−t)ˆi+(2−t)4ˆj,1<t≤2
42)
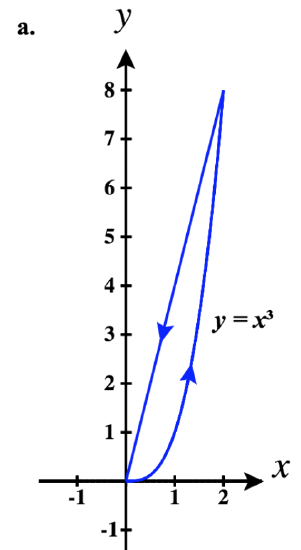
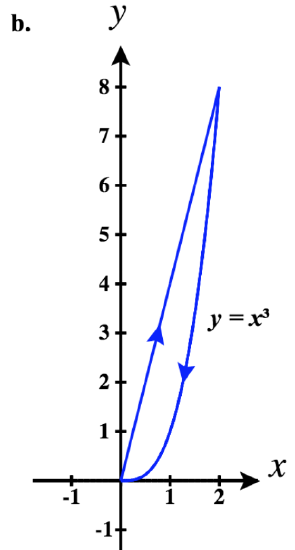
43)
- Answer
- a. ⇀r1(t)=tˆi+0ˆj for 0≤t≤2
⇀r2(t)=−tˆi+(2+t)ˆj for −2≤t≤−1
⇀r3(t)=−tˆi+(−t)3ˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi,0≤t≤2(4−t)ˆi+(t−2)ˆj,2<t≤3(4−t)ˆi+(4−t)3ˆj,3<t≤4
b. ⇀r1(t)=tˆi+t3ˆj for 0≤t≤1
⇀r2(t)=tˆi+(2−t)ˆj for 1≤t≤2
⇀r3(t)=−tˆi+0ˆj for −2≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+t3ˆj,0≤t≤1tˆi+(2−t)ˆj,1<t≤2(4−t)ˆi,2<t≤4
44)