2.4: The Unit Tangent and the Unit Normal Vectors
- Page ID
- 592
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The derivative of a vector valued function gives a new vector valued function that is tangent to the defined curve. The analog to the slope of the tangent line is the direction of the tangent line. Since a vector contains a magnitude and a direction, the velocity vector contains more information than we need. We can strip a vector of its magnitude by dividing by its magnitude.
Definition: Unit Tangent Vector
Let \(\textbf{r}(t)\) be a differentiable vector valued function and \(\textbf{v}(t)=\textbf{r}'(t)\) be the velocity vector. Then we define the unit tangent vector by as the unit vector in the direction of the velocity vector.
\[ \textbf{T}(t) = \dfrac{v(t)}{||v(t)||} \]
Example \(\PageIndex{1}\)
Let
\[\textbf{r}(t) = t \hat{\textbf{i}} + e^t \hat{\textbf{j}} - 3t^2 \hat{\textbf{k}} . \nonumber\]
Find \(\textbf{T}(t)\) and \(\textbf{T}(0)\).
Solution
We have
\[\textbf{v}(t) = \textbf{r}'(t) = \hat{\textbf{i}} + e^t \hat{\textbf{j}} - 6t \hat{\textbf{k}} \nonumber\]
and
\[ || v(t)|| = \sqrt{1+e^{2t}+36t^2} . \nonumber\]
To find the unit tangent vector, we just divide
\[T(t)=\dfrac{v(t)}{||V(T)||} = \dfrac{ \hat{\textbf{i}} + e^t \hat{\textbf{j}} - 6t \hat{\textbf{k}} }{\sqrt{1+e^{2t} + 36t^2}} . \nonumber\]
To find \(T(0)\) plug in 0 to get
\[\begin{align*} T(0) &= \dfrac{ \hat{\textbf{i}} + e^0 \hat{\textbf{j}} - 6(0) \hat{\textbf{k}} }{ \sqrt{1+e^{2(0)}+36(0)^2 } } \\ &= \dfrac{ \hat{\textbf{i}} + \hat{\textbf{j}} }{\sqrt{2}} \\ &= \dfrac{1}{\sqrt{2}} \hat{\textbf{i}} + \dfrac{1}{\sqrt{2}} \hat{\textbf{j}} . \end{align*}\]
The Principal Unit Normal Vector
A normal vector is a perpendicular vector. Given a vector v in the space, there are infinitely many perpendicular vectors. Our goal is to select a special vector that is normal to the unit tangent vector. Geometrically, for a non straight curve, this vector is the unique vector that point into the curve. Algebraically we can compute the vector using the following definition.
Definition: Principal Unit Normal Vector
Let r(t) be a differentiable vector valued function and let T(t) be the unit tangent vector. Then the principal unit normal vector N(t) is defined by
\[ \textbf{N}(t) = \dfrac{\textbf{T}'(t)}{||\textbf{T}'(t)||} .\]
Comparing this with the formula for the unit tangent vector, if we think of the unit tangent vector as a vector valued function, then the principal unit normal vector is the unit tangent vector of the unit tangent vector function. You will find that finding the principal unit normal vector is almost always cumbersome. The quotient rule usually rears its ugly head.
Example \(\PageIndex{2}\)
Find the unit normal vector for the vector valued function
\[\textbf{r}(t)= t \hat{\textbf{i}} + t^2 \hat{\textbf{j}} \nonumber\]
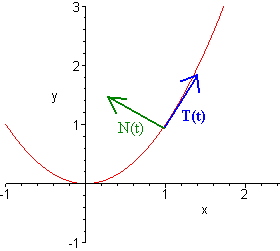
and sketch the curve, the unit tangent and unit normal vectors when \(t = 1\).
Solution
First we find the unit tangent vector
\[\textbf{T}(t)=\dfrac{ \hat{\textbf{i}} + 2t \hat{\textbf{j}} }{\sqrt{1+4t^2}}. \nonumber\]
Now use the quotient rule to find \(\textbf{T}'(t)\)
\[\textbf{T}'(t)=\dfrac{ (1+4t^2)^{\frac{1}{2}} (2 \hat{\textbf{j}} ) - ( \hat{\textbf{i}}+ 2t \hat{\textbf{j}} ) 4t (1+4t^2)^{-\frac{1}{2}}}{1+4t^2}.\nonumber \]
Since the unit vector in the direction of a given vector will be the same after multiplying the vector by a positive scalar, we can simplify by multiplying by the factor
\[(1+4t^2)(1+4t^2)^{\frac{1}{2}}. \nonumber\]
The first factor gets rid of the denominator and the second factor gets rid of the fractional power. We have
\[\begin{align*} \textbf{T}'(t)(1+4t^2)(1+4t^2)^{\frac{1}{2}} &= (1+4t^2)(2 \hat{\textbf{j}}) - ( \hat{\textbf{i}} + 2t\hat{\textbf{j}})4t \\ &=-4t \hat{\textbf{i}} + 2 \hat{\textbf{j}}. \end{align*}\]
Now we divide by the magnitude (after first dividing by 2) to get
\[N(t) = \dfrac{-2t \hat{\textbf{i}}+ \hat{\textbf{j}} }{ \sqrt{1+4t^2} }. \nonumber\]
Now plug in \(t=1\) for both the unit tangent vector to get
\[\textbf{T}(1) = \dfrac{1}{\sqrt{5}} \hat{\textbf{i}} + \dfrac{2}{\sqrt{5}} \hat{\textbf{j}} \]
and
\[ \textbf{N}(1) = -\dfrac{2}{\sqrt{5}} \hat{\textbf{i}} + \dfrac{1}{\sqrt{5}} \hat{\textbf{j}} . \nonumber\]
The picture below shows the graph and the two vectors.
Tangential and Normal Components of Acceleration
Imagine yourself driving down from Echo Summit towards Myers and having your brakes fail. As you are riding you will experience two forces (other than the force of terror) that will change the velocity. The force of gravity will cause the car to increase in speed. A second change in velocity will be caused by the car going around the curve. The first component of acceleration is called the tangential component of acceleration and the second is called the normal component of acceleration. As you may guess the tangential component of acceleration is in the direction of the unit tangent vector and the normal component of acceleration is in the direction of the principal unit normal vector. Once T and N is known, it is straightforward to find the two components. We have:
Definition: Tangential and Normal Components of Acceleration
The tangential component of acceleration is
\[a_t = a \cdot \textbf{T} = \dfrac{v \cdot a }{||v||} \]
and the normal component of acceleration is
\[ a_N = a \cdot \textbf{N} = \dfrac{||v \times a|| }{||v||} \]
and
\[ \textbf{a} = a_N \textbf{N} + a_T \textbf{T}. \]
Proof
First notice that
\[\textbf{v} = ||\textbf{v}|| \textbf{T} \;\;\; \text{and} \;\;\; \textbf{T}' = ||\textbf{T}'||\textbf{N}. \label{proof1}\]
Taking the derivative of both sides gives
\[\textbf{a} = \textbf{v}' = ||\textbf{v}||' \textbf{T} + ||\textbf{v}|| \textbf{T}' = ||\textbf{v}||' \textbf{T} + ||\textbf{v}|| ||\textbf{T}'|| \textbf{N}. \label{proof2}\]
This tells us that the acceleration vector is in the plane that contains the unit tangent vector and the unit normal vector. The equality in Equation \ref{proof1} follows immediately from the definition of the component of a vector in the direction of another vector. The equalities in Equation \ref{proof2} will be left as exercises.
\(\square\)
Example \(\PageIndex{3}\)
Find the tangential and normal components of acceleration for the prior example
\[ \textbf{r}(t) = t \hat{\textbf{i}} + t^2 \hat{\textbf{j}}. \nonumber \]
Solution
Taking two derivatives, we have
\[ \textbf{a}(t) = \textbf{r}'' (t) = 2 \hat{\textbf{j}}. \nonumber\]
We dot the acceleration vector with the unit tangent and normal vectors to get
\[a_T (t) = \textbf{a} \cdot \textbf{T} = \dfrac{4t}{\sqrt{1+4t^2}}, \nonumber\]
\[a_N (t) = \textbf{a} \cdot \textbf{N} = \dfrac{2}{\sqrt{1+4t^2}}. \nonumber\]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


