9.3: Orthogonality

Using the inner product, we can now define the notion of orthogonality, prove that the Pythagorean theorem holds in any inner product space, and use the Cauchy-Schwarz inequality to prove the triangle inequality. In particular, this will show that $\norm{v}=\sqrt{\inner{v}{v}}$ does indeed define a norm.

Definition 9.3.1. Two vectors $u,v\in V$ are orthogonal (denoted $u\bot v$) if $\inner{u}{v}=0$.

Note that the zero vector is the only vector that is orthogonal to itself. In fact, the zero vector is orthogonal to every vector $v\in V$.

Theorem 9.3.2. (Pythagorean Theorem). If $u,v\in V$, an inner product space, with $u\bot v$, then $\norm{\cdot}$ defined by $\norm{v}:=\sqrt{\inner{v}{v}}$ obeys

$$\norm{u+v}^2 = \norm{u}^2 + \norm{v}^2.$$

Proof. Suppose $u,v\in V$ such that $u\bot v$. Then
$$\begin{equation*} \begin{split} \norm{u+v}^2 &= \inner{u+v}{u+v} = \norm{u}^2 + \norm{v}^2 + \inner{u}{v} + \inner{v}{u}\\ &= \norm{u}^2 + \norm{v}^2. \end{split} \end{equation*}$$

Note that the converse of the Pythagorean Theorem holds for real vector spaces since, in that case, $\inner{u}{v}+\inner{v}{u}=2\mathrm{Re} \inner{u}{v} =0$.

Given two vectors $u,v\in V$ with $v\neq 0$, we can uniquely decompose $u$ into two pieces: one piece parallel to $v$ and one piece orthogonal to $v$. This is called an orthogonal decomposition. More precisely, we have
$$\begin{equation*} u=u_1+u_2, \end{equation*}$$
where $u_1=a v$ and $u_2\bot v$ for some scalar $a \in \mathbb{F}$. To obtain such a decomposition, write $u_2=u-u_1=u-av$. Then, for $u_2$ to be
orthogonal to $v$, we need
$$\begin{equation*} 0 = \inner{u-av}{v} = \inner{u}{v} - a\norm{v}^2. \end{equation*}$$
Solving for $a$ yields $a=\inner{u}{v}/\norm{v}^2$ so that
$$\begin{equation}\label{eq:orthogonal decomp} u=\frac{\inner{u}{v}}{\norm{v}^2} v + \left( u-\frac{\inner{u}{v}}{\norm{v}^2} v \right). \tag{9.3.1} \end{equation}$$

This decomposition is particularly useful since it allows us to provide a simple proof for the Cauchy-Schwarz inequality.

Theorem 9.3.3 (Cauchy-Schwarz inequality). Given any $u,v\in V$, we have

$$|\inner{u}{v}| \le \norm{u} \norm{v}.$$

Furthermore, equality holds if and only if $u$ and $v$ are linearly dependent, i.e., are scalar multiples of each other.

Proof. If $v=0$, then both sides of the inequality are zero. Hence, assume that $v\neq 0$, and consider the orthogonal decomposition
$$\begin{equation*} u = \frac{\inner{u}{v}}{\norm{v}^2} v + w \end{equation*}$$
where $w\bot v$. By the Pythagorean theorem, we have
$$\begin{equation*} \norm{u}^2 = \left\| \frac{\inner{u}{v}}{\norm{v}^2}v \right\|^2 + \norm{w}^2 = \frac{|\inner{u}{v}|^2}{\norm{v}^2} + \norm{w}^2 \ge \frac{|\inner{u}{v}|^2}{\norm{v}^2}. \end{equation*}$$
Multiplying both sides by $\norm{v}^2$ and taking the square root then yields the Cauchy-Schwarz inequality.
Note that we get equality in the above arguments if and only if $w=0$. But, by Equation (9.3.1), this means that $u$ and $v$ are linearly dependent.

The Cauchy-Schwarz inequality has many different proofs. Here is another one.

Alternate Proof of Theorem 9.3.3. Given $u,v\in V$, consider the norm square of the vector $u+r e^{i\theta}v:$
$$\begin{equation*} 0 \le \norm{u+re^{i\theta}v}^2 = \norm{u}^2 + r^2 \norm{v}^2 + 2 \mathrm{Re} (r e^{i\theta} \inner{u}{v}). \end{equation*}$$
Since $\inner{u}{v}$ is a complex number, one can choose $\theta$ so that $e^{i \theta} \inner{u}{v}$ is real. Hence, the right hand side is a parabola $a r^2 +b r +c$ with real coefficients. It will lie above the real axis, i.e. $ar^2+br+c\ge 0$, if it does not have any real solutions for $r$. This is the case when the discriminant satisfies $b^2-4ac\le 0$. In our case this means
$$\begin{equation*} 4 | \inner{u}{v} |^2 -4 \norm{u}^2 \norm{v}^2\le 0. \end{equation*}$$

Moreover, equality only holds if $r$ can be chosen such that $u+r e^{i\theta} v =0$, which means that $u$ and $v$ are scalar multiples.

Now that we have proven the Cauchy-Schwarz inequality, we are finally able to verify the triangle inequality. This is the final step in showing that $\norm{v}=\sqrt{\inner{v}{v}}$ does indeed define a norm. We illustrate the triangle inequality in Figure 9.3.1.

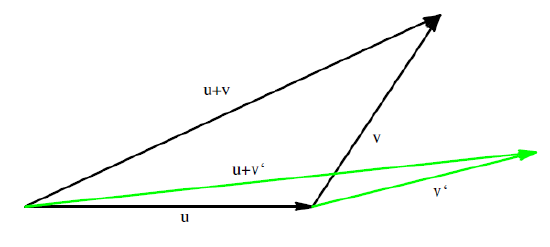
Figure 9.3.1: The Triangle Inequality in $\mathbb{R^2}$

Theorem 9.3.4. (Triangle Inequality). For all $u,v\in V$ we have

$$\norm{u+v} \le \norm{u} + \norm{v}.$$

Proof. By a straightforward calculation, we obtain
$$\begin{equation*} \begin{split} \norm{u+v}^2 &= \inner{u+v}{u+v} = \inner{u}{u} + \inner{v}{v} +\inner{u}{v} + \inner{v}{u}\\ &= \inner{u}{u} + \inner{v}{v} + \inner{u}{v} +\overline{\inner{u}{v}} = \norm{u}^2 + \norm{v}^2 +2 \mathrm{Re} \inner{u}{v}. \end{split} \end{equation*}$$
Note that $\mathrm{Re}\inner{u}{v}\le |\inner{u}{v}|$ so that, using the Cauchy-Schwarz inequality, we obtain
$$\begin{equation*} \norm{u+v}^2 \le \norm{u}^2 + \norm{v}^2 + 2\norm{u}\norm{v} = (\norm{u}+\norm{v})^2. \end{equation*}$$
Taking the square root of both sides now gives the triangle inequality.

Remark 9.3.5. Note that equality holds for the triangle inequality if and only if $v=ru$ or $u=rv$ for some $r\ge 0$. Namely, equality in the proof happens only if $\inner{u}{v} =\norm{u}\norm{v}$, which is equivalent to $u$ and $v$ being scalar multiples of one another.

Theorem 9.3.6. (Parallelogram Law). Given any $u,v\in V$, we have
$$\norm{u+v}^2 + \norm{u-v}^2 = 2(\norm{u}^2 + \norm{v}^2).$$

Proof. By direct calculation,
$$\begin{equation*} \begin{split} \norm{u+v}^2 + \norm{u-v}^2 &= \inner{u+v}{u+v} + \inner{u-v}{u-v}\\ &= \norm{u}^2 + \norm{v}^2 + \inner{u}{v} + \inner{v}{u} + \norm{u}^2 + \norm{v}^2 - \inner{u}{v} -\inner{v}{u}\\ &=2(\norm{u}^2 + \norm{v}^2). \end{split} \end{equation*}$$

Remark 9.3.7. We illustrate the parallelogram law in Figure 9.3.2.

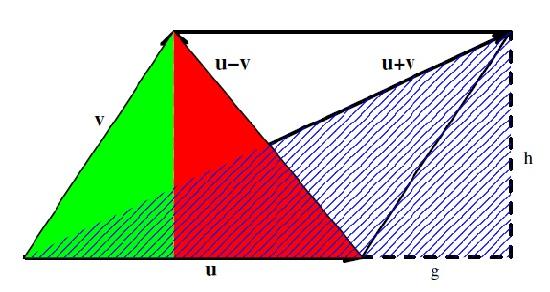
Figure 9.3.2: The Parallelogram Law in $\mathbb{R^2}$

Contributors

• Isaiah Lankham, Mathematics Department at UC Davis
• Bruno Nachtergaele, Mathematics Department at UC Davis
• Anne Schilling, Mathematics Department at UC Davis

Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.