1.6: Subtract Whole Numbers (Part 2)
- Page ID
- 5769
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Translate Word Phrases to Math Notation
As with addition, word phrases can tell us to operate on two numbers using subtraction. To translate from a word phrase to math notation, we look for key words that indicate subtraction. Some of the words that indicate subtraction are listed in Table \(\PageIndex{1}\).
| Operation | Word Phrase | Example | Expression |
|---|---|---|---|
| Subtraction | minus | 5 minus 1 | 5 - 1 |
| difference | the difference of 9 and 4 | 9 - 4 | |
| decreased by | 7 decreased by 3 | 7 - 3 | |
| less than | 5 less than 8 | 8 - 5 | |
| subtracted from | 1 subtracted from 6 | 6 - 1 |
Translate and then simplify:
- the difference of \(13\) and \(8\)
- subtract \(24\) from \(43\)
Solution
- The word difference tells us to subtract the two numbers. The numbers stay in the same order as in the phrase.
| the difference of 13 and 8 | |
| Translate. | 13 - 8 |
| Simplify. | 5 |
- The words subtract from tells us to take the second number away from the first. We must be careful to get the order correct.
| subtract 24 from 43 | |
| Translate. | 43 - 24 |
| Simplify. | 19 |
Translate and simplify:
- the difference of \(14\) and \(9\)
- subtract \(21\) from \(37\)
- Answer a
-
\(14-9=5\)
- Answer b
-
\(37-21=16\)
Translate and simplify:
- \(11\) decreased by \(6\)
- \(18\) less than \(67\)
- Answer a
-
\(11-6=5\)
- Answer b
-
\(67-18=49\)
Subtract Whole Numbers in Applications
To solve applications with subtraction, we will use the same plan that we used with addition. First, we need to determine what we are asked to find. Then we write a phrase that gives the information to find it. We translate the phrase into math notation and then simplify to get the answer. Finally, we write a sentence to answer the question, using the appropriate units.
The temperature in Chicago one morning was \(73\) degrees Fahrenheit. A cold front arrived and by noon the temperature was \(27\) degrees Fahrenheit. What was the difference between the temperature in the morning and the temperature at noon?
Solution
We are asked to find the difference between the morning temperature and the noon temperature.
| Write a phrase. | the difference of 73 and 27 |
| Translate to math notation. Difference tells us to subtract. | 73 - 27 |
| Then we do the subtraction. | 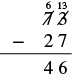 |
| Write a sentence to answer the question. | The difference in temperatures was 46 degrees Fahrenheit. |
The high temperature on June \(1^{st}\) in Boston was \(77\) degrees Fahrenheit, and the low temperature was \(58\) degrees Fahrenheit. What was the difference between the high and low temperatures?
- Answer
-
The difference is \(19\) degrees Fahrenheit.
The weather forecast for June \(2^{nd}\) in St Louis predicts a high temperature of \(90\) degrees Fahrenheit and a low of \(73\) degrees Fahrenheit. What is the difference between the predicted high and low temperatures?
- Answer
-
The difference is \(17\) degrees Fahrenheit.
A washing machine is on sale for \($399\). Its regular price is \($588\). What is the difference between the regular price and the sale price?
Solution
We are asked to find the difference between the regular price and the sale price.
| Write a phrase | the difference between 588 and 399 |
| Translate to math notation | 588 - 399 |
| Subtract | 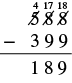 |
| Write a sentence to answer the question | The difference between the regular price and the sale price is $189. |
A television set is on sale for \($499\). Its regular price is \($648\). What is the difference between the regular price and the sale price?
- Answer
-
The difference is \($149\).
A patio set is on sale for \($149\). Its regular price is \($285\). What is the difference between the regular price and the sale price?
- Answer
-
The difference is \($136\).
Access Additional Online Resources
Key Concepts
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
| Subtraction | seven minus three | the difference of |
- Subtract whole numbers
- Write the numbers so each place value lines up vertically.
- Subtract the digits in each place value. Work from right to left starting with the ones place. If the digit on top is less than the digit below, borrow as needed.
- Continue subtracting each place value from right to left, borrowing if needed.
- Check by adding.
Glossary
- difference
-
The difference is the result of subtracting two or more numbers.
Practice Makes Perfect
Use Subtraction Notation
In the following exercises, translate from math notation to words.
- 15 - 9
- 18 - 16
- 42 - 35
- 83 - 64
- 675 - 350
- 790 - 525
Model Subtraction of Whole Numbers
In the following exercises, model the subtraction.
- 5 - 2
- 8 - 4
- 6 - 3
- 7 - 5
- 18 - 5
- 19 - 8
- 17 - 8
- 17 - 9
- 35 - 13
- 32 - 11
- 61 - 47
- 55 - 36
Subtract Whole Numbers
In the following exercises, subtract and then check by adding.
- 9 - 4
- 9 - 3
- 8 - 0
- 2 - 0
- 38 - 16
- 45 - 21
- 85 - 52
- 99 - 47
- 493 - 370
- 268 - 106
- 5,946 - 4,625
- 7,775 - 3,251
- 75 - 47
- 63 - 59
- 461 - 239
- 486 - 257
- 525 - 179
- 542 - 288
- 6,318 - 2,799
- 8,153 - 3,978
- 2,150 - 964
- 4,245 - 899
- 43,650 - 8,982
- 35,162 - 7,885
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate and simplify.
- The difference of 10 and 3
- The difference of 12 and 8
- The difference of 15 and 4
- The difference of 18 and 7
- Subtract 6 from 9
- Subtract 8 from 9
- Subtract 28 from 75
- Subtract 59 from 81
- 45 decreased by 20
- 37 decreased by 24
- 92 decreased by 67
- 75 decreased by 49
- 12 less than 16
- 15 less than 19
- 38 less than 61
- 47 less than 62
Mixed Practice
In the following exercises, simplify.
- 76−47
- 91 − 53
- 256 − 184
- 305 − 262
- 719 + 341
- 647 + 528
- 2,015 − 1,993
- 2,020 − 1,984
In the following exercises, translate and simplify.
- Seventy-five more than thirty-five
- Sixty more than ninety-three
- 13 less than 41
- 28 less than 36
- The difference of 100 and 76
- The difference of 1,000 and 945
Subtract Whole Numbers in Applications
In the following exercises, solve.
- Temperature The high temperature on June 2 in Las Vegas was 80 degrees and the low temperature was 63 degrees. What was the difference between the high and low temperatures?
- Temperature The high temperature on June 1 in Phoenix was 97 degrees and the low was 73 degrees. What was the difference between the high and low temperatures?
- Class size Olivia’s third grade class has 35 children. Last year, her second grade class had 22 children. What is the difference between the number of children in Olivia’s third grade class and her second grade class?
- Class size There are 82 students in the school band and 46 in the school orchestra. What is the difference between the number of students in the band and the orchestra?
- Shopping A mountain bike is on sale for $399. Its regular price is $650. What is the difference between the regular price and the sale price?
- Shopping A mattress set is on sale for $755. Its regular price is $1,600. What is the difference between the regular price and the sale price?
- Savings John wants to buy a laptop that costs $840. He has $685 in his savings account. How much more does he need to save in order to buy the laptop?
- Banking Mason had $1,125 in his checking account. He spent $892. How much money does he have left?
Everyday Math
- Road trip Noah was driving from Philadelphia to Cincinnati, a distance of 502 miles. He drove 115 miles, stopped for gas, and then drove another 230 miles before lunch. How many more miles did he have to travel?
- Test Scores Sara needs 350 points to pass her course. She scored 75, 50, 70, and 80 on her first four tests. How many more points does Sara need to pass the course?
Writing Exercises
- Explain how subtraction and addition are related.
- How does knowing addition facts help you to subtract numbers?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section
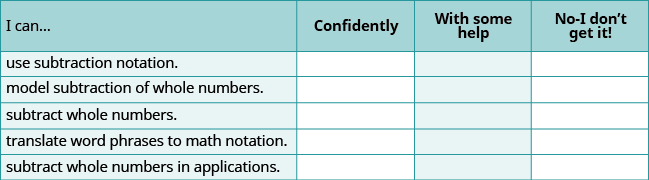
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


