5.5: Decimals and Fractions (Part 1)
- Page ID
- 5000
- Convert fractions to decimals
- Order decimals and fractions
- Simplify expressions using the order of operations
- Find the circumference and area of circles
Before you get started, take this readiness quiz.
- Divide: 0.24 ÷ 8. If you missed this problem, review Example 5.4.9.
- Order 0.64__0.6 using < or >. If you missed this problem, review Example 5.2.7.
- Order −0.2__−0.1 using < or >. If you missed this problem, review Example 5.2.8.
Convert Fractions to Decimals
In Decimals, we learned to convert decimals to fractions. Now we will do the reverse—convert fractions to decimals. Remember that the fraction bar indicates division. So \(\dfrac{4}{5}\) can be written 4 ÷ 5 or \(5 \overline{)4}\). This means that we can convert a fraction to a decimal by treating it as a division problem.
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
Write the fraction \(\dfrac{3}{4}\) as a decimal.
Solution
| A fraction bar means division, so we can write the fraction 3 4 using division. | 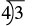 |
| Divide. | 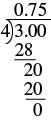 |
So the fraction \(\dfrac{3}{4}\) is equal to 0.75.
Write the fraction as a decimal: \(\dfrac{1}{4}\).
- Answer
-
\(0.25\)
Write the fraction as a decimal: \(\dfrac{3}{8}\).
- Answer
-
\(0.375\)
Write the fraction \(− \dfrac{7}{2}\) as a decimal.
Solution
| The value of this fraction is negative. After dividing, the value of the decimal will be negative. We do the division ignoring the sign, and then write the negative sign in the answer. | $$- \dfrac{7}{2}$$ |
| Divide 7 by 2. | 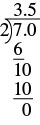 |
So, \(− \dfrac{7}{2}\) = −3.5.
Write the fraction as a decimal: \(− \dfrac{9}{4}\).
- Answer
-
\(-2.25\)
Write the fraction as a decimal: \(− \dfrac{11}{2}\).
- Answer
-
\(-5.5\)
Repeating Decimals
So far, in all the examples converting fractions to decimals the division resulted in a remainder of zero. This is not always the case. Let’s see what happens when we convert the fraction \(\dfrac{4}{3}\) to a decimal. First, notice that \(\dfrac{4}{3}\) is an improper fraction. Its value is greater than 1. The equivalent decimal will also be greater than 1.
We divide 4 by 3.
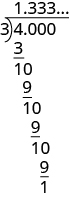
No matter how many more zeros we write, there will always be a remainder of 1, and the threes in the quotient will go on forever. The number 1.333… is called a repeating decimal. Remember that the “…” means that the pattern repeats.
A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.
How do you know how many ‘repeats’ to write? Instead of writing 1.333 … we use a shorthand notation by placing a line over the digits that repeat. The repeating decimal 1.333 … is written 1.\(\overline{3}\). The line above the 3 tells you that the 3 repeats endlessly. So 1.333… = 1.\(\overline{3}\). For other decimals, two or more digits might repeat. Table \(\PageIndex{1}\) shows some more examples of repeating decimals.
| 1.333… = 1.\(\overline{3}\) | 3 is the repeating digit |
| 4.1666… = 4.1\(\overline{6}\) | 6 is the repeating digit |
| 4.161616… = 4.\(\overline{16}\) | 16 is the repeating block |
| 0.271271271… = 0.\(\overline{271}\) | 271 is the repeating block |
Write \(\dfrac{43}{22}\) as a decimal.
Solution
Divide 43 by 22.
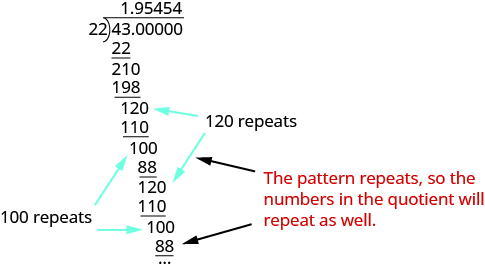
Notice that the differences of 120 and 100 repeat, so there is a repeat in the digits of the quotient; 54 will repeat endlessly. The first decimal place in the quotient, 9, is not part of the pattern. So,
\[\dfrac{43}{22} = 1.9 \overline{54}\]
Write as a decimal: \(\dfrac{27}{11}\).
- Answer
-
\(2. \overline{45}\)
Write as a decimal: \(\dfrac{51}{22}\).
- Answer
-
\(2.3 \overline{18}\)
It is useful to convert between fractions and decimals when we need to add or subtract numbers in different forms. To add a fraction and a decimal, for example, we would need to either convert the fraction to a decimal or the decimal to a fraction.
Simplify: \(\dfrac{7}{8}\) + 6.4.
Solution
| Change \(\dfrac{7}{8}\) to a decimal. |  |
0.875 + 6.4 |
| Add. | 7.275 |
Simplify: \(\dfrac{3}{8}\) + 4.9.
- Answer
-
\(5.275\)
Simplify: 5.7 + \(\dfrac{13}{20}\).
- Answer
-
\(6.35\)
Order Decimals and Fractions
In Decimals, we compared two decimals and determined which was larger. To compare a decimal to a fraction, we will first convert the fraction to a decimal and then compare the decimals.
Order \(\dfrac{3}{8}\)__0.4 using < or >.
Solution
| Convert \(\dfrac{3}{8}\) to a decimal. | 0.375__0.4 |
| Compare 0.375 to 0.4 | 0.375 < 0.4 |
| Rewrite with the original fraction. | \(\dfrac{3}{8}\) < 0.4 |
Order each of the following pairs of numbers, using < or >.
\[\dfrac{17}{20} \_ \_ \; 0.82\]
- Answer
-
\(>\)
Order each of the following pairs of numbers, using < or >.
\[\dfrac{3}{4} \_ \_ \; 0.785\]
- Answer
-
\(<\)
When ordering negative numbers, remember that larger numbers are to the right on the number line and any positive number is greater than any negative number.
Order −0.5___\(− \dfrac{3}{4}\) using < or >.
Solution
| Convert \(− \dfrac{3}{4}\) to a decimal. | −0.5___−0.75 |
| Compare −0.5 to −0.75. | −0.5 > −0.75 |
| Rewrite the inequality with the original fraction. | −0.5 > \(− \dfrac{3}{4}\) |
Order each of the following pairs of numbers, using < or >:
\[− \dfrac{5}{8} \_ \_ −0.58\]
- Answer
-
\(<\)
Order each of the following pairs of numbers, using < or >:
\[−0.53 \_ \_ − \dfrac{11}{20}\]
- Answer
-
\(>\)
Write the numbers \(\dfrac{13}{20}\), 0.61, \(\dfrac{11}{16}\) in order from smallest to largest.
Solution
| Convert the fractions to decimals. | 0.65, 0.61, 0.6875 |
| Write the smallest decimal number first. | 0.61, ____, _____ |
| Write the next larger decimal number in the middle place. | 0.61, 0.65, _____ |
| Write the last decimal number (the larger) in the third place. | 0.61, 0.65, 0.6875 |
| Rewrite the list with the original fractions. | 0.61, \(\dfrac{13}{20}, \dfrac{11}{16}\) |
Write each set of numbers in order from smallest to largest: \(\dfrac{7}{8}, \dfrac{4}{5}\), 0.82.
- Answer
-
\(\frac{4}{5}\), \(0.82\), \(\frac{7}{8}\)
Write each set of numbers in order from smallest to largest: 0.835, \(\dfrac{13}{16}, \dfrac{3}{4}\).
- Answer
-
\(\frac{3}{4}\), \(\frac{13}{16}\), \(0.835\)
Simplify Expressions Using the Order of Operations
The order of operations introduced in Use the Language of Algebra also applies to decimals. Do you remember what the phrase “Please excuse my dear Aunt Sally” stands for?
Simplify the expressions: (a) 7(18.3 − 21.7) (b) \(\dfrac{2}{3}\) (8.3 − 3.8)
Solution
(a) 7(18.3 − 21.7)
| Simplify inside parentheses. | 7(−3.4) |
| Multiply. | −23.8 |
(b) \(\dfrac{2}{3}\) (8.3 − 3.8)
| Simplify inside parentheses. | $$\dfrac{2}{3} (4.5)$$ |
| Write 4.5 as a fraction. | $$\dfrac{2}{3} \left(\dfrac{4.5}{1}\right)$$ |
| Multiply. | $$\dfrac{9}{3}$$ |
| Simplify. | $$3$$ |
Simplify: (a) 8(14.6 − 37.5) (b) \(\dfrac{3}{5}\) (9.6 − 2.1).
- Answer a
-
\(-183.2\)
- Answer b
-
\(4.5\)
Simplify: (a) 25(25.69 − 56.74) (b) \(\dfrac{2}{7}\) (11.9 − 4.2).
- Answer a
-
\(-776.25\)
- Answer b
-
\(2.2\)
Simplify each expression: (a) 6 ÷ 0.6 + (0.2)4 − (0.1)2 (b) \(\left(\dfrac{1}{10}\right)^{2}\) + (3.5)(0.9)
Solution
(a) 6 ÷ 0.6 + (0.2)4 − (0.1)2
| Simplify exponents. | 6 ÷ 0.6 + (0.2)4 − 0.01 |
| Divide. | 10 + (0.2)4 − 0.01 |
| Multiply. | 10 + 0.8 − 0.01 |
| Add. | 10.8 − 0.01 |
| Subtract. | 10.79 |
(b) \(\left(\dfrac{1}{10}\right)^{2}\) + (3.5)(0.9)
| Simplify exponents. | \(\dfrac{1}{100}\) + (3.5)(0.9) |
| Multiply. | \(\dfrac{1}{100}\) + 3.15 |
| Convert \(\dfrac{1}{100}\) to a decimal. | 0.01 + 3.15 |
| Add. | 3.16 |
Simplify: 9 ÷ 0.9 + (0.4)3 − (0.2)2.
- Answer
-
\(11.16\)
Simplify: \(\left(\dfrac{1}{2}\right)^{2}\) + (0.3)(4.2).
- Answer
-
\(1.51\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


