4.2E: Graphs of Exponential Functions (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section 4.2 Exercise
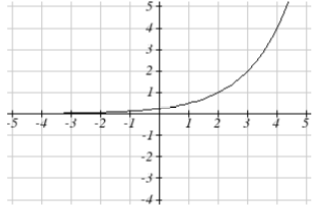
Match each function with one of the graphs below.
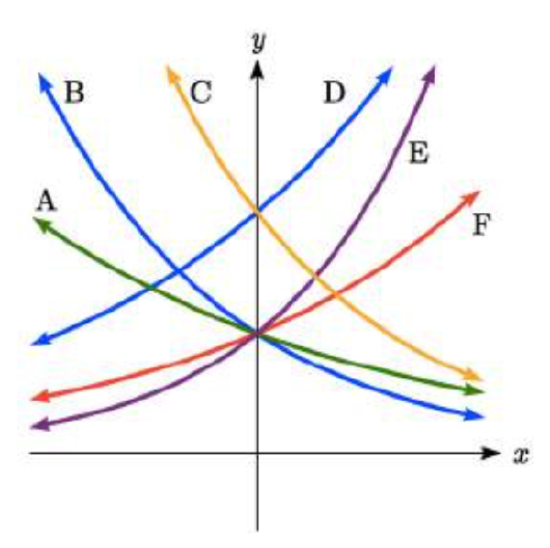
1. f(x)=2(0.69)x
2. f(x)=2(1.28)x
3. f(x)=2(0.81)x
4. f(x)=4(1.28)x
5. f(x)=2(1.59)x
6. f(x)=4(0.69)x
If all the graphs to the right have equations with form f(x)=abx,
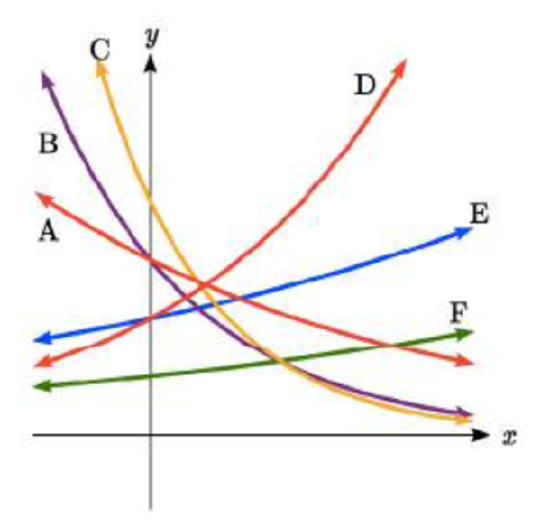
7. Which graph has the largest value for b?
8. Which graph has the smallest value for b?
9. Which graph has the largest value for a?
10. Which graph has the smallest value for a?
Sketch a graph of each of the following transformations of f(x)=2x
11. f(x)=2−x
12. g(x)=−2x
13. h(x)=2x+3
14. f(x)=2x−4
15. f(x)=2x−2
16. k(x)=2x−3
Starting with the graph of f(x)=4x, find a formula for the function that results from
17. Shifting f(x) 4 units upwards
18. Shifting f(x) 3 units downwards
19. Shifting f(x) 2 units left
20. Shifting f(x) 5 units right
21. Reflecting f(x) about the x-axis
22. Reflecting f(x) about the y-axis
Describe the long run behavior, as x→∞ and x→−∞ of each function
23. f(x)=−5(4x)−1
24. f(x)=−2(3x)+2
25. f(x)=3(12)x−2
26. f(x)=4(14)x+1
27. f(x)=3(4)−x+2
28. f(x)=−2(3)−x−1
Find a formula for each function graphed as a transformation of f(x)=2x.
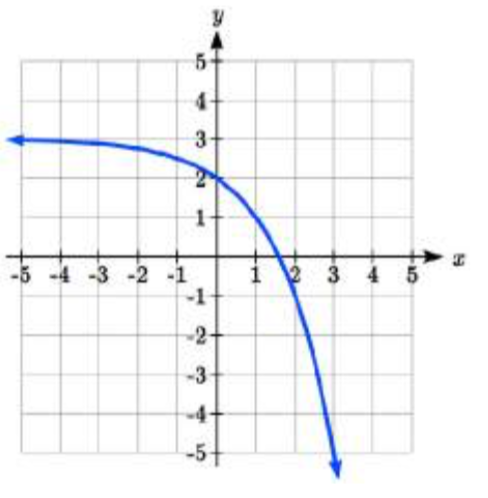
29. 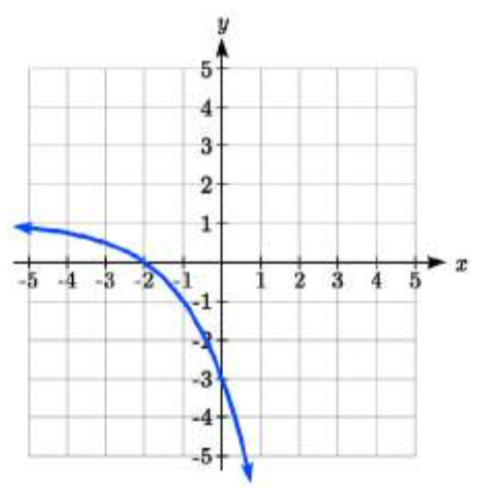 30.
30. 
31. 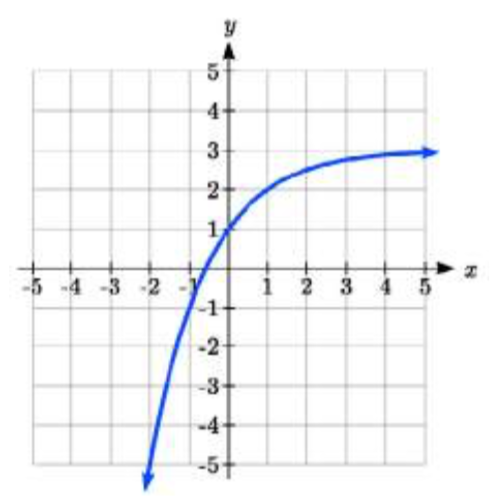 32.
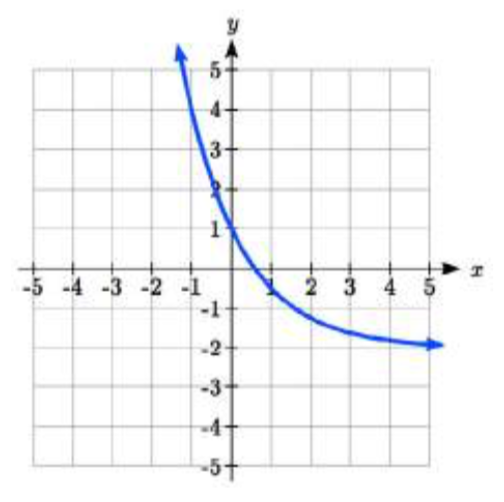
32. 
Find an equation for the exponential function graphed.
33. 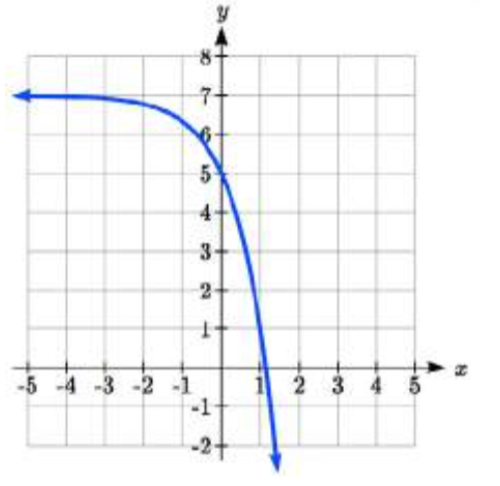 34.
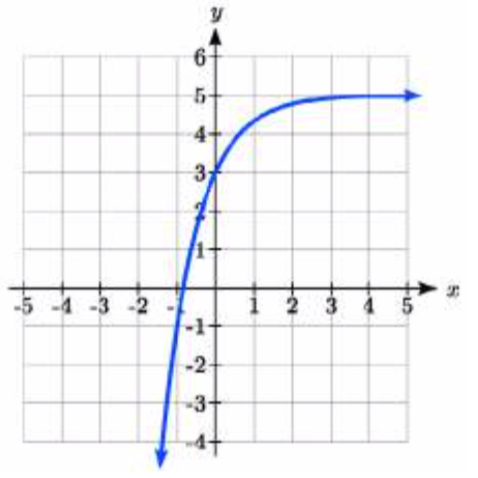
34. 
35. 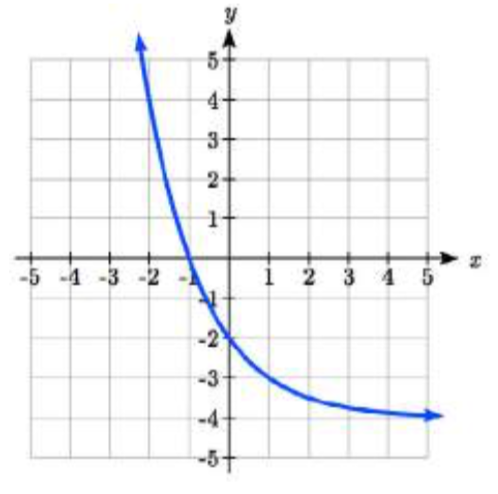 36.
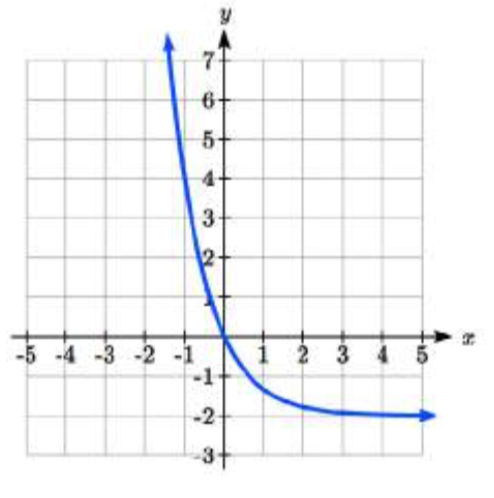
36. 
- Answer
-
1. B
3. A
5. E
7. D
9. C
11.
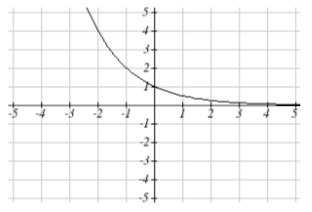
13.
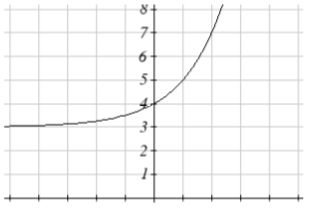
15.
17. y=4x+4
19. y=4x+2
21. y=−4x
23. As x→∞, f(x)→−∞. As x→−∞ f(x)→−1
25. As x→∞, f(x)→−2. As x→−∞ f(x)→∞
27. As x→∞, f(x)→2. As x→−∞ f(x)→∞
29. y=−2x+2+1=−4(2)x+1
31. y=−2(2)−x+3
33. y=−2(3)x+7
35. y=2(12)x−4


