6.8: Composition of Functions

Nothing goes by luck in composition. It allows of no tricks.

Henry David Thoreau (1817–1862), American author

The term “composition” is a name that mathematicians use for an idea that comes up fairly often in everyday life.

Example \(6.8.1\).

1. The father of the mother of a person is the grandfather of the person. (To be precise, it is the maternal grandfather of the person — and his or her other grandfather is paternal.) To express the relationship in a mathematical formula, we can write: \[\forall x,(\operatorname{grandfather}(x)=\text { father }(\operatorname{mother}(x))) .\]
   A mathematician abbreviates this formula by writing \[\text { grandfather }=\text { father } \circ \text { mother }\]
   and says that the (maternal) \(\text {grandfather}\) function is the composition of \(\text {father}\) and \(\text {mother}\).
2. The brother of the mother of a person is an uncle of the person, so \(\text {uncle}\) is the composition of \(\text {brother}\) and \(\text {mother}\): \[\forall x,(\text { uncle }(x)=\operatorname{brother}(\operatorname{mother}(x))) ,\]
   or, more briefly, \[\text { uncle }=\text { brother o mother. }\]
   (For the sake of this example, let us ignore the issue that \(\text {uncle}\) and \(\text {brother}\) are not functions, because some people have no uncle or no brother, or have more than one.)
3. The daughter of a child is a granddaughter, so \(\text {granddaughter}\) is a composition of \(\text {daughter}\) and \(\text {child}\): \[\text { granddaughter }=\text { daughter } \circ \text { child. }\]
   (We ignore the fact that \(\text {granddaughter}\), \(\text {daughter}\), and \(\text {child}\) are not functions.)

Exercise \(6.8.2\).

State the usual name for each composition. (Ignore the fact that \(\text {sister}\), \(\text {daughter}\), and many of the other relations are not functions.)

1. \(\text { husband } \circ \text{ sister }=\)
2. \(\text { husband } \circ \text{ mother }=\)
3. \(\text { husband } \circ \text{ wife }=\)
4. \(\text { husband } \circ \text{ daughter }=\)
5. \(\text { mother } \circ \text{ sister }=\)
6. \(\text { daughter } \circ \text{ sister }=\)
7. \(\text { parent } \circ \text{ parent }=\)
8. \(\text { child } \circ \text{ child }=\)
9. \(\text { parent } \circ \text{ parent } \circ \text { parent }=\)
10. \(\text { child } \circ \text{ brother } \circ \text { parent }=\)

Definition \(6.8.3\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\). The composition \(g \circ f\) of \(g\) and \(f\) is the function from \(A\) to \(C\) defined by \[(g \circ f)(a)=g(f(a)) \text { for all } a \in A .\]

Example \(6.8.4\).

Define f: \mathbb{R} \rightarrow \mathbb{R}\) and \(g: \mathbb{R} \rightarrow \mathbb{R}\) by \(f(x) = 3x\) and \(g(x) = x^{2}\). Then \(g \circ f\) and \(f \circ g\) are functions from \(\mathbb{R} \text { to } \mathbb{R}\). For all \(x \in \mathbb{R}\), we have \[(g \circ f)(x)=g(f(x))=g(3 x)=(3 x)^{2}=9 x^{2}\]

and \[(f \circ g)(x)=f(g(x))=f\left(x^{2}\right)=3\left(x^{2}\right)=3 x^{2} .\]

Notice that (in this example) \(f \circ g \neq g \circ f\), so composition is not commutative.

Exercise \(6.8.5\).

The formulas define functions \(f\) and \(g\) from \(\mathbb{R} \text { to } \mathbb{R}\). Find formulas for \((f \circ g)(x)\) and \((g \circ f)(x)\).

1. \(f(x)=3 x+1 \text { and } g(x)=x^{2}+2 .\)
2. \(f(x)=3 x+1 \text { and } g(x)=(x-1) / 3 .\)
3. \(f(x)=a x+b \text { and } g(x)=c x+d \text { (where } a, b, c, d \in \mathbb{R}) .\)
4. \(f(x)=|x| \text { and } g(x)=x^{2} .\)
5. \(f(x)=|x| \text { and } g(x)=-x .\)

WARNING. To calculate the value of the function \(g \circ f\) at the point \(a\), do not begin by calculating \(g(a)\). Instead, you need to calculate \(f(a)\). Then plug that value into the function \(g\).

Example \(6.8.6\).

Figure \(6C\) provides an arrow diagram to illustrate the composition \(g \circ f\).

• Starting from any point of \(A\), follow the arrow (for the function \(f\)) that starts there to arrive at some point of \(B\).
• Then follow the arrow (for the function \(g\)) that starts there to arrive at a point of \(C\).

For example, the \(f\)-arrow from \(a\) leads to \(m\) and the \(g\)-arrow from \(m\) leads to \(u\). So \((g \circ f)(a) = u\).

Figure \(6C\). Arrows for the composition \(g \circ f\) are dotted.

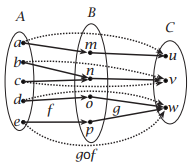
Notice that even though \(g\) appears on the left in the expression \(g \circ f\), the arrow diagram for \(g\) appears on the right in the figure. This is an unfortunate consequence of the way that we calculate \(g(f(x))\) — see the warning above.

Exercise \(6.8.7\).

Let \(A = \{1, 2, 3, 4\}\), \(B = \{a, b, c, d\}\), and \(C = \{\)♣, ♦, ♥, ♠\(\}\). The sets of ordered pairs in each part are functions \(f: A \rightarrow B\) and \(g: B \rightarrow C\). Represent \(g \circ f\) as a set of ordered pairs.

1. \(f=\{(1, \mathrm{a}),(2, \mathrm{~b}),(3, \mathrm{c}),(4, \mathrm{~d})\}\), \(g = \){(a, ♣),(b, ♦),(c, ♥),(d, ♠)}
2. \(f=\{(1, \mathrm{a}),(2, \mathrm{~b}),(3, \mathrm{c}),(4, \mathrm{~d})\}\), \(g = \){(a, ♣),(b, ♣),(c, ♣),(d, ♣)}
3. \(f=\{(1, \mathrm{~b}),(2, \mathrm{c}),(3, \mathrm{~d}),(4, \mathrm{a})\}\), \(g = \){(a, ♣),(b, ♠),(c, ♥),(d, ♦)}
4. \(f=\{(1, \mathrm{a}),(2, \mathrm{~b}),(3, \mathrm{c}),(4, \mathrm{~d})\}\), \(g = \){(a, ♣),(b, ♣),(c, ♥),(d, ♠)}
5. \(f=\{(1, \mathrm{a}),(2, \mathrm{~b}),(3, \mathrm{a}),(4, \mathrm{~b})\}\), \(g = \){(a, ♣),(b, ♣),(c, ♥),(d, ♠)}

Exercise \(6.8.8\).

The definition of \(g \circ f\) requires that the domain of \(g\) is equal to the codomain of \(f\). (They are both called \(B\) in the definition, so they are required to be equal.) Why?

Here are some examples of proofs that combine composition with other important ideas that we have seen.

Example \(6.8.9\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\). Show that if \(g \circ f\) is one-to-one, then \(f\) is one-to-one.

Solution

Given \(a_{1}, a_{2} \in A\), such that \(f(a_{1}) = f(a_{2})\), we have \[g\left(f\left(a_{1}\right)\right)=g\left(f\left(a_{2}\right)\right) ,\]

so \[(g \circ f)\left(a_{1}\right)=(g \circ f)\left(a_{2}\right) .\]

Since \(g \circ f\) is one-to-one, this implies \(a_{1} = a_{2}\). So \(f\) is one-to-one.

Example \(6.8.10\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\). Show that if \(f\) and \(g\) are onto, then \(g \circ f\) is onto.

Solution

Let \(c\) be an arbitrary element of \(C\). Since \(g\) is onto, there is some \(b \in B\0, such that \(g(b) = c\). Then, since \(f\) is onto, there is some \(a \in A\), such that \(f(a) = b\). Therefore \[(g \circ f)(a)=g(f(a))=g(b)=c .\]

Since \(c\) is an arbitrary element of \(C\), this implies that \(g \circ f\) is onto.

Example \(6.8.11\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\). Show that if \(f\) and \(g \circ f\) are bijections, then g is a bijection.

Solution

It suffices to show that \(g\) is both one-to-one and onto.

(one-to-one) Let \(b_{1}\) and \(b_{2}\) be arbitrary elements of \(B\), such that \(g(b_{1}) = g(b_{2})\). Since \(f\) is a bijection, it is onto, so there exist \(a_{1}, a_{2} \in A\), such that \(f(a_{1}) = b_{1}\) and \(f(a_{2}) = b_{2}\). Then \[(g \circ f)\left(a_{1}\right)=g\left(f\left(a_{1}\right)\right)=g\left(b_{1}\right)=g\left(b_{2}\right)=g\left(f\left(a_{2}\right)\right)=(g \circ f)\left(a_{2}\right) .\]
Since \(g \circ f\) is a bijection, it is one-to-one, so we conclude that \(a_{1} = a_{2}\). Therefore \[b_{1}=f\left(a_{1}\right)=f\left(a_{2}\right)=b_{2} .\]
Since \(b_{1}\) and \(b_{2}\) are arbitrary elements of \(B\), such that \(g(b_{1}) = g(b_{2})\), this implies that \(g\) is one-to-one.

(onto) Let \(c\) be an arbitrary element of \(C\). Since \(g \circ f\) is a bijection, it is onto, so there exists \(a \in A\), such that \((g \circ f)(a) = c\). Let \(b = f(a)\). Then \[g(b)=g(f(a))=(g \circ f)(a)=c .\]
Since \(c\) is an arbitrary element of \(C\), we conclude that \(g\) is onto.

Exercise \(6.8.12\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\).

1. Show that if \(f\) and \(g\) are bijections, then \(g \circ f\) is a bijection.
2. Show that if \(g\) and \(g \circ f\) are bijections, then \(f\) is a bijection.
3. Show that if \(f\) and \(g\) are bijections, then \((g \circ f)^{−1} = f^{−1} \circ g^{−1}.

Exercise \(6.8.13\).

Assume \(f: A \rightarrow B\) and \(g: B \rightarrow A\) (and see Notation \(6.6.8\) for the definition of the identity maps \(I_{A}\) and \(I_{B}\)).

1. Show that \(g\) is the inverse of \(f\) if and only if \(f \circ g = I_{B}\) and \(g \circ f = I_{A}\).
2. What are \(f \circ I_{A}\) and \(I_{B} \circ f\)?

Exercise \(6.8.14\).

1. Give an example of functions \(f: A \rightarrow B\) and \(g: B \rightarrow C\), such that \(g \circ f\) is onto, but \(f\) is not onto. [Hint: Let \(A = B = \mathbb{R}\), \(C = [0, \infty)\), \(f(x) = x^{2}\), and \(g(x) = x^{2}\).]
2. Define \(f: [0, \infty) \rightarrow \mathbb{R}\) by \(f(x) = x\) and \(g :\mathbb{R} \rightarrow \mathbb{R}\) by \(g(x) = |x|\). Show that \(g \circ f\) is one-to-one, but \(g\) is not one-to-one.
3. (harder) Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow C\). Write a definition of \(g \circ f\) purely in terms of sets of ordered pairs. That is, find a predicate \(P(x, y)\), such that \[g \circ f=\{(a, c) \in A \times C \mid P(a, c)\} .\]
   The predicate cannot use the notation \(f(x)\) or \(g(x)\). Instead, it should refer to the ordered pairs that are elements of \(f\) and \(g\).