7.1: Binary Relations

Recall that, by definition, any function \(f : A \rightarrow B\) is a set of ordered pairs. More precisely, each element of \(f\) is an ordered pair \((a, b)\), such that \(a \in A\) and \(b \in B\). Therefore, every element of \(f\) is an element of \(A \times B\), so \(f\) is a subset of \(A \times B\). \[\text { Every function from } A \text { to } B \text { is a subset of } A \times B \text {. }\]

Example \(7.1.1\).

The function \(\text {mother: PEOPLE } \rightarrow \text { PEOPLE }\) is represented by the set \[\{(p, m) \in \text { PEOPLE } \times \text { PEOPLE } \mid m \text { is the mother of } p\} .\]

Many other relationships can also be represented by subsets of \(\text {PEOPLE } \times \text { PEOPLE}\), even though they are not functions. For example, son is not a function, because some people have more than one son (or because some people have no sons at all). However, we can represent this relation by the set \[\{(p, s) \in \text { PEOPLE } \times \text { PEOPLE } \mid s \text { is a son of } p\} .\]

In fact, any relationship that you can define between two people (or, to say this in the official language of logic, any binary predicate on the set \(\text {PEOPLE}\)) can be represented by a subset of \(\text {PEOPLE } \times \text { PEOPLE}\). A few examples of possible relationships are:

• \(x\) is a sister of \(y\)
• \(x\) knew \(y\) in high school
• \(x\) is taller than \(y\)
• \(x\) and \(y\) are in the same math class
• etc.

In recognition of this, mathematicians simply define a relation to be a set of ordered pairs; that is, a relation is any subset of \(A \times B\). Unlike the case of functions, there are no restrictions — every subset is a relation.

Definition \(7.1.2\).

Suppose \(A\) and \(B\) are sets.

1. Any subset of \(A \times B\) is called a relation from \(A\) to \(B\).
2. For the special case where \(A = B\), any subset of \(A \times A\) is called a binary relation on \(A\).

We will mostly be concerned with binary relations, not relations from some set \(A\) to some other set \(B\).

Example \(7.1.3\).

Some examples of binary relations on \(\text {PEOPLE}\) are: \(\text {brother, sister, aunt, uncle, mother, father, grandfather, cousin, etc.}\)

Definition \(7.1.4\).

We can draw a picture to represent any given binary relation on any given set \(A\):

• Draw a dot for each element of \(A\).
• For \(a, b \in A\), draw an arrow from \(a\) to \(b\) if and only if \((a, b)\) is an element of the relation.

The resulting picture is called a digraph. (The word is pronounced “DIE-graff” — it is short for “directed graph.”)

Example \(7.1.5\).

Let \(A = \{1, 2, 3, 4, 5\}\). We can define a binary relation \(R\) on \(A\) by letting \[R=\left\{(x, y) \mid x^{2}+y<10\right\} .\]

This binary relation is represented by the following digraph:

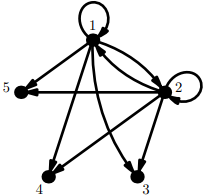
For example, note that \((x, 4) \in R \text { iff } x \in\{1,2\}\), and the digraph has arrows from 1 to 4 and from 2 to 4.

Exercise \(7.1.6\).

Let \(B\) be the set consisting of you, your siblings, your parents, and your grandparents. Draw a digraph that represents each of the following binary relations on \(B\).

1. The relation “has ever had the same last name as.”
2. The relation “is a child of.”
3. The relation “has ever been married to.”

Example \(7.1.7\).

This book (like other mathematics textbooks) deals mainly with relations on sets of mathematical objects. Here are a few well-known examples:

1. The less-than relation “\(<\)” is a binary relation on \(\mathbb{R}\).
   That is, for any real numbers \(x\) and \(y\), the assertion \(x < y\) is either true or false.
2. The equality relation “\(=\)” is a binary relation on the entire universe of discourse \(\mathcal{U}\).
3. The subset relation “\(\subset\)” is a binary relation on the collection of all sets in \(\mathcal{U}\).
4. The relation “\(x\) is disjoint from \(y\)” is also a binary relation on the collection of all sets in \(\mathcal{U}\).

Notation \(7.1.8\).

Suppose \(R\) is a binary relation on a set \(A\). For \(a_{1}, a_{2} \in A\):

1. To signify that \((a_{1}, a_{2}) \in R\), we may write \(a_{1} R a_{2}\).
2. To signify that \(\left(a_{1}, a_{2}\right) \notin R\), we may write \(a_{1} \not R a_{2}\).

There are three basic properties that any given binary relation may or may not have:

Definition \(7.1.9\).

Suppose \(R\) is a binary relation on a set \(A\).

1. We say that \(R\) is reflexive iff \(\forall a \in A,(a R a)\).
2. We say that \(R\) is symmetric iff \(\forall a, b \in A,((a R b) \Rightarrow(b R a))\).
3. We say that \(R\) is transitive iff \(\forall a, b, c \in A,(((a R b) \&(b R c)) \Rightarrow(a R c))\).

Example \(7.1.10\).

1. “\(=\)” is reflexive, symmetric, and transitive.“
2. "\(<\)” is transitive, but neither reflexive nor symmetric.
3. “\(\subset\)” is transitive and reflexive, but not symmetric.

Example \(7.1.12\).

Consider the following binary relation \(R\) on \(\{1, 2, 3\}\): \[R=\{(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)\}\]

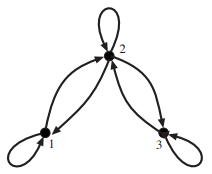
1. \(R\) is reflexive, because \(1 R 1,2 R 2,\), and \(3 R 3\).
2. \(R\) is symmetric, because, for each \((a, b) \in R\), the reversal \((b, a)\) is also in \(R\).
3. \(R\) is not transitive, because \(1 R 2\) and \(2 R 3\), but \(1 \not R 3\).

Exercise \(7.1.12\).

Find binary relations on \(\{1, 2, 3\}\) that are:

1. symmetric, but neither reflexive nor transitive.
2. reflexive, but neither symmetric nor transitive.
3. transitive and symmetric, but not reflexive.
4. neither reflexive, nor symmetric, nor transitive.

(Express each relation as a set of ordered pairs, draw the corresponding digraph, and briefly justify your answers.)