7.1: Introduction to the Laplace Transform

Definition of the Laplace Transform

To define the Laplace transform, we first recall the definition of an improper integral. If \(g\) is integrable over the interval \([a,T]\) for every \(T>a\), then the improper integral of \(g\) over \([a,\infty)\) is defined as

\[\label{eq:8.1.1} \int^\infty_a g(t)\,dt=\lim_{T\to\infty}\int^T_a g(t)\,dt.\]

We say that the improper integral converges if the limit in Equation \ref{eq:8.1.1} exists; otherwise, we say that the improper integral diverges or does not exist. Here’s the definition of the Laplace transform of a function \(f\).

Defintion 7.1.1 : Laplace transform

Let \(f\) be defined for \(t\ge0\) and let \(s\) be a real number. Then the Laplace transform of \(f\) is the function \(F\) defined by

\[\label{eq:8.1.2} F(s)=\int_0^\infty e^{-st} f(t)\,dt,\]

for those values of \(s\) for which the improper integral converges.

It is important to keep in mind that the variable of integration in Equation \ref{eq:8.1.2} is \(t\), while \(s\) is a parameter independent of \(t\). We use \(t\) as the independent variable for \(f\) because in applications the Laplace transform is usually applied to functions of time.

The Laplace transform can be viewed as an operator \({\cal L}\) that transforms the function \(f=f(t)\) into the function \(F=F(s)\). Thus, Equation \ref{eq:8.1.2} can be expressed as

\[F={\cal L}(f).\nonumber \]

The functions \(f\) and \(F\) form a transform pair, which we’ll sometimes denote by

\[f(t)\leftrightarrow F(s).\nonumber\]

It can be shown that if \(F(s)\) is defined for \(s=s_0\) then it is defined for all \(s>s_0\) (Exercise 8.1.14b).

Computation of Some Simple Laplace Transforms

Example 7.1.1

Find the Laplace transform of \(f(t)=1\).

Solution

From Equation \ref{eq:8.1.2} with \(f(t)=1\),

\[F(s)=\int_0^\infty e^{-st}\,dt=\lim_{T\to\infty}\int_0^T e^{-st}\, dt.\nonumber\]

If \(s\ne 0\) then

\[\label{eq:8.1.3} \int_0^T e^{-st}dt=-{1\over s}e^{-st}\Big|_0^T={1-e^{-sT}\over s}.\]

Therefore

\[\label{eq:8.1.4} \lim_{T\to\infty}\int_0^T e^{-st}dt=\left\{\begin{array}{rr} {1\over s}, & s>0,\\ \infty, & s<0. \end{array}\right.\]

If \(s=0\) the integrand reduces to the constant \(1\), and

\[\lim_{T\to\infty}\int_0^T 1\,dt=\lim_{T\to\infty}\int_0^T 1\,dt= \lim_{T\to\infty}T=\infty.\nonumber\]

Therefore \(F(0)\) is undefined, and

\[F(s)=\int_0^\infty e^{-st}dt={1\over s},\quad s>0.\nonumber\]

This result can be written in operator notation as

\[{\cal L}(1)={1\over s},\quad s>0,\nonumber\]

or as the transform pair

\[1\leftrightarrow{1\over s},\quad s>0.\nonumber\]

Note

It is convenient to combine the steps of integrating from \(0\) to \(T\) and letting \(T → ∞\). Therefore, instead of writing Equation \ref{eq:8.1.3} and \ref{eq:8.1.4} as separate steps we write

\[\int_{0}^{\infty} e^{-s t} d t=-\left.\frac{1}{s} e^{-s t}\right|_{0} ^{\infty}=\left\{\begin{array}{cl}{\frac{1}{s},} & {s>0} \\ {\infty,} & {s<0}\end{array}\right. \nonumber\]

We'll follow this practice throughout this chapter.

Example 7.1.2

Find the Laplace transform of \(f(t)=t\).

From Equation \ref{eq:8.1.2} with \(f(t)=t\),

\[\label{eq:8.1.5} F(s)=\int_0^\infty e^{-st}t\,dt.\]

If \(s\ne0\), integrating by parts yields

\[\begin{align*} \int_0^\infty e^{-st}t\,dt&=-{te^{-st}\over s}\bigg|_0^\infty +{1\over s}\int_0^\infty e^{-st}\,dt =-\left[{t\over s}+{1\over s^2}\right]e^{-st}\bigg|_0^\infty \\&=\left\{\begin{array}{rr} {1\over s^2},\quad s>0,\\ \infty,\,s<0.\end{array}\right.\end{align*}\nonumber\]

If \(s=0\), the integral in Equation \ref{eq:8.1.5} becomes

\[\int_0^\infty t\,dt={t^2\over2}\bigg|_0^\infty=\infty.\nonumber\]

Therefore \(F(0)\) is undefined and

\[F(s)={1\over s^2},\quad s>0.\nonumber\]

This result can also be written as

\[{\cal L}(t)={1\over s^2},\quad s>0,\nonumber\]

or as the transform pair

\[t\leftrightarrow{1\over s^2},\quad s>0.\nonumber\]

Example 7.1.3 :

Find the Laplace transform of \(f(t)=e^{at}\), where \(a\) is a constant.

From Equation \ref{eq:8.1.2} with \(f(t)=e^{at}\),

\[F(s)=\int_0^\infty e^{-st}e^{at}\,dt.\nonumber\]

Combining the exponentials yields

\[F(s)=\int_0^\infty e^{-(s-a)t}\,dt.\nonumber\]

However, we know from Example 7.1.1 that

\[\int_0^\infty e^{-st}\,dt={1\over s},\quad s>0.\nonumber\]

Replacing \(s\) by \(s-a\) here shows that

\[F(s)={1\over s-a},\quad s>a.\nonumber\]

This can also be written as

\[{\cal L}(e^{at})={1\over s-a},\quad s>a, \text{ or } e^{at}\leftrightarrow{1\over s-a},\quad s>a.\nonumber\]

Example 7.1.4

[Find the Laplace transforms of \(f(t)=\sin\omega t\) and \(g(t)=\cos\omega t\), where \(\omega\) is a constant.

Define

\[\label{eq:8.1.6} F(s)=\int_0^\infty e^{-st}\sin\omega t\,dt\]

and

\[\label{eq:8.1.7} G(s)=\int_0^\infty e^{-st}\cos\omega t\,dt.\]

If \(s>0\), integrating Equation \ref{eq:8.1.6} by parts yields

\[F(s)=-{e^{-st}\over s}\sin\omega t\Big|_0^\infty+{\omega\over s} \int_0^\infty e^{-st}\cos\omega t\,dt,\nonumber\]

so

\[\label{eq:8.1.8} F(s)={\omega\over s}G(s).\]

If \(s>0\), integrating Equation \ref{eq:8.1.7} by parts yields

\[G(s)=-{e^{-st}\cos\omega t\over s}\Big|_0^\infty - {\omega\over s} \int_0^\infty e^{-st}\sin\omega t\,dt,\nonumber\]

so

\[G(s)={1\over s} - {\omega\over s} F(s).\nonumber\]

Now substitute from Equation \ref{eq:8.1.8} into this to obtain

\[G(s)={1\over s} - {\omega^2\over s^2} G(s).\nonumber\]

Solving this for \(G(s)\) yields

\[G(s)={s\over s^2+\omega^2},\quad s>0.\nonumber\]

This and Equation \ref{eq:8.1.8} imply that

\[F(s)={\omega\over s^2+\omega^2},\quad s>0.\nonumber\]

Tables of Laplace Transforms

Extensive tables of Laplace transforms have been compiled and are commonly used in applications. The brief table of Laplace transforms in the Appendix will be adequate for our purposes.

Example 7.1.5

Use the table of Laplace transforms to find \({\cal L}(t^3e^{4t})\).

The table includes the transform pair

\[t^ne^{at}\leftrightarrow {n!\over(s-a)^{n+1}}.\nonumber\]

Setting \(n=3\) and \(a=4\) here yields

\[\cal L (t^3e^{4t})={3!\over(s-4)^4}={6\over(s-4)^4}.\nonumber\]

We’ll sometimes write Laplace transforms of specific functions without explicitly stating how they are obtained. In such cases you should refer to the table of Laplace transforms.

Linearity of the Laplace Transform

The next theorem presents an important property of the Laplace transform.

Theorem 7.1.2 Linearity Property

Suppose \({\cal L}(f_i)\) is defined for \(s>s_i,\) \(1\le i\le n).\) Let \(s_0\) be the largest of the numbers \(s_1\), \(s_{2},\) …,\(s_n,\) and let \(c_1\), \(c_2\),…, \(c_n\) be constants. Then

\[{\cal L}(c_1f_1+c_2f_2+\cdots+c_nf_n)=c_1{\cal L}(f_1)+c_2{\cal L}(f_2) +\cdots+c_n{\cal L}(f_n)\mbox{ for } s>s_0.\nonumber\]

Proof

We give the proof for the case where \(n=2\). If \(s>s_0\) then

\[\begin{aligned} {\cal L}(c_1f_1+c_2f_2)&= \int_0^\infty e^{-st}\left(c_1f_1(t)+c_2f_2(t))\right)\,dt\\ &= c_1\int_0^\infty e^{-st}f_1(t)\,dt+c_2\int_0^\infty e^{-st}f_2(t)\,dt\\ &= c_1{\cal L}(f_1)+c_2{\cal L}(f_2).\end{aligned}\nonumber\]

Example 7.1.6

Use Theorem 7.1.2 and the known Laplace transform

\[{\cal L}(e^{at})={1\over s-a} \nonumber\]

to find \({\cal L}(\cosh bt)\,(b\ne0)\).

Solution

By definition,

\[\cosh bt={e^{bt}+e^{-bt}\over 2}. \nonumber\]

Therefore

\[\label{eq:8.1.9} \begin{array}{ccl} {\cal L}(\cosh bt)&=& {\cal L}\left( {1\over 2} e^{bt}+ {1\over 2}e^{-bt}\right)\\[4pt] &=& {1\over 2} {\cal L}(e^{bt}) + {1\over 2} {\cal L}(e^{-bt}) \qquad \hbox{(linearity property)}\\[4pt] &=& {1\over 2}\, {1\over s-b} + {1\over 2}\, {1\over s+b}, \end{array}\]

where the first transform on the right is defined for \(s>b\) and the second for \(s>-b\); hence, both are defined for \(s>|b|\). Simplifying the last expression in Equation \ref{eq:8.1.9} yields

\[{\cal L}(\cosh bt)={s\over s^2-b^2},\quad s>|b|.\nonumber\]

The next theorem enables us to start with known transform pairs and derive others. (For other results of this kind, see Exercises 8.1.6 and 8.1.13.)

Theorem 7.1.3 First Shifting Theorem

If

\[\label{eq:8.1.10} F(s)=\int_0^\infty e^{-st} f(t)\,dt\]

is the Laplace transform of \(f(t)\) for \(s>s_0\), then \(F(s-a)\) is the Laplace transform of \(e^{at}f(t)\) for \(s >s_0+a\).

Proof

Replacing \(s\) by \(s-a\) in Equation \ref{eq:8.1.10} yields

\[\label{eq:8.1.11} F(s-a)=\int_0^\infty e^{-(s-a)t}f(t)\,dt\]

if \(s-a>s_0\); that is, if \(s>s_0+a\). However, Equation \ref{eq:8.1.11} can be rewritten as

\[F(s-a)=\int_0^\infty e^{-st}\left(e^{at}f(t)\right)\,dt,\nonumber\]

which implies the conclusion.

Example 7.1.7

Use Theorem 7.1.3 and the known Laplace transforms of \(1\), \(t\), \(\cos\omega t\), and \(\sin\omega t\) to find

\[{\cal L}(e^{at}),\quad {\cal L}(te^{at}),\quad {\cal L}(e^{\lambda t}\sin \omega t),\mbox{and } {\cal L}(e^{\lambda t}\cos\omega t).\nonumber\]

Solution

In the following table the known transform pairs are listed on the left and the required transform pairs listed on the right are obtained by applying Theorem 7.1.3 .

Table 7.1.1

\(f(t)\leftrightarrow F(s)\)	\(e^{at}f(t)\leftrightarrow F(s-a)\)
\(1\leftrightarrow {1\over s},\quad s>0\)	\(e^{at}\leftrightarrow {1\over(s-a)},\quad s>a\)
\(t\leftrightarrow \frac{1}{s^{2}},\quad s>0\)	\(te^{at}\leftrightarrow \frac{1}{(s-a)^{2}},\quad s>a\)
\(\sin\omega t\leftrightarrow \frac{\omega }{s^{2}+\omega ^{2}},\quad s>0\)	\(e^{\lambda t}\sin\omega t\leftrightarrow \frac{\omega}{(s-\lambda)^{2}+\omega ^{2}},\quad s>\lambda\)
\(\cos\omega t\leftrightarrow \frac{s}{s^{2}+\omega ^{2}},\quad s>0\)	\(e^{\lambda t}\sin\omega t\leftrightarrow \frac{s-\lambda }{(s-\lambda )^{2}+\omega ^{2}},\quad s>\lambda\)

Existence of Laplace Transforms

Not every function has a Laplace transform. For example, it can be shown (Exercise 8.1.3) that

\[\int_0^\infty e^{-st}e^{t^2} dt=\infty\nonumber\]

for every real number \(s\). Hence, the function \(f(t)=e^{t^2}\) does not have a Laplace transform.

Our next objective is to establish conditions that ensure the existence of the Laplace transform of a function. We first review some relevant definitions from calculus.

Recall that a limit

\[\lim_{t\to t_0} f(t)\nonumber\]

exists if and only if the one-sided limits

\[\lim_{t\to t_0-}f(t)\quad \text{and} \quad \lim_{t\to t_0+}f(t)\nonumber\]

both exist and are equal; in this case,

\[\lim_{t\to t_0}f(t)=\lim_{t\to t_0-}f(t)=\lim_{t\to t_0+}f(t) .\nonumber\]

Recall also that \(f\) is continuous at a point \(t_0\) in an open interval \((a,b)\) if and only if

\[\lim_{t\to t_0}f(t)=f(t_0),\nonumber\]

which is equivalent to

\[\label{eq:8.1.12} \lim_{t\to t_0+}f(t)=\lim_{t\to t_0-}f(t)=f(t_0).\]

For simplicity, we define

\[f(t_0+)=\lim_{t\to t_0+}f(t)\quad\hbox{and }\quad f(t_0-)=\lim_{t\to t_0-}f(t),\nonumber\]

so Equation \ref{eq:8.1.12} can be expressed as

\[f(t_0+)=f(t_0-)=f(t_0).\nonumber\]

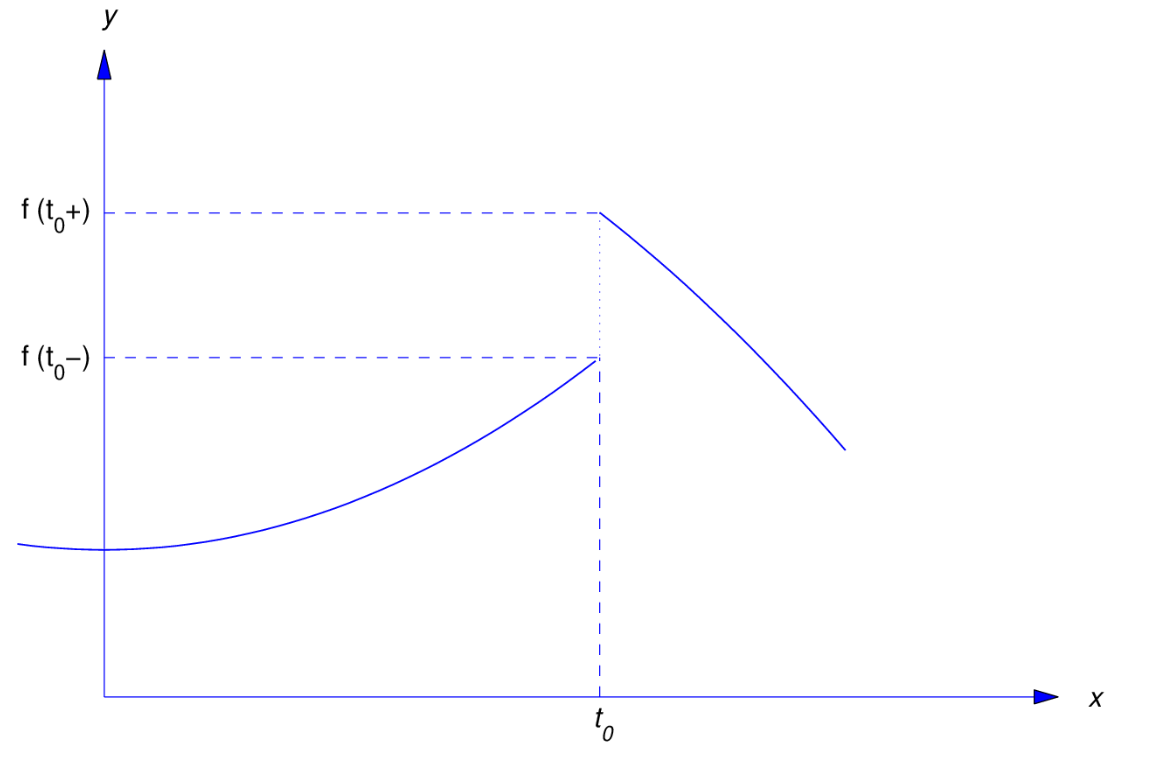
If \(f(t_0+)\) and \(f(t_0-)\) have finite but distinct values, we say that \(f\) has a jump discontinuity at \(t_0\), and

\[f(t_0+)-f(t_0-)\nonumber\]

is called the jump in \(f\) at \(t_0\) (Figure 7.1.1 ).

Figure 7.1.1 : A jump discontinuity.

If \(f(t_0+)\) and \(f(t_0-)\) are finite and equal, but either \(f\) isn’t defined at \(t_0\) or it is defined but

\[f(t_0)\ne f(t_0+)=f(t_0-),\nonumber\]

we say that \(f\) has a removable discontinuity at \(t_0\) (Figure 7.1.2 ). This terminolgy is appropriate since a function \(f\) with a removable discontinuity at \(t_0\) can be made continuous at \(t_0\) by defining (or redefining)

\[f(t_0)=f(t_0+)=f(t_0-).\nonumber\]

Note

We know from calculus that a definite integral isn’t affected by changing the values of its integrand at isolated points. Therefore, redefining a function f to make it continuous at removable discontinuities does not change \(\cal{L}(f)\).

Theorem 7.1.4 Piecewise Continuous

• A function \(f\) is said to be piecewise continuous on a finite closed interval \([0,T]\) if \(f(0+)\) and \(f(T-)\) are finite and \(f\) is continuous on the open interval \((0,T)\) except possibly at finitely many points, where \(f\) may have jump discontinuities or removable discontinuities.
• A function \(f\) is said to be piecewise continuous on the infinite interval \([0,\infty)\) if it is piecewise continuous on \([0,T]\) for every \(T>0\).

Figure 7.1.3 shows the graph of a typical piecewise continuous function.

It is shown in calculus that if a function is piecewise continuous on a finite closed interval then it is integrable on that interval. But if \(f\) is piecewise continuous on \([0,\infty)\), then so is \(e^{-st}f (t)\), and therefore

\[\int_0^T e^{-st}f(t)\,dt \nonumber\]

Figure 7.1.2

Figure 7.1.3

exists for every \(T>0\). However, piecewise continuity alone does not guarantee that the improper integral

\[\label{eq:8.1.13} \int_0^\infty e^{-st}f(t)\,dt=\lim_{T\to\infty}\int_0^T e^{-st}f(t)\, dt\]

converges for \(s\) in some interval \((s_0,\infty)\). For example, we noted earlier that Equation \ref{eq:8.1.13} diverges for all \(s\) if \(f(t)=e^{t^2}\). Stated informally, this occurs because \(e^{t^2}\) increases too rapidly as \(t\to\infty\). The next definition provides a constraint on the growth of a function that guarantees convergence of its Laplace transform for \(s\) in some interval \((s_0,\infty)\).

Theorem 7.1.5 : of exponential order

A function \(f\) is said to be of exponential order \(s_0\) if there are constants \(M\) and \(t_0\) such that

\[\label{eq:8.1.14} |f(t)|\le Me^{s_0t},\quad t\ge t_0.\]

In situations where the specific value of \(s_0\) is irrelevant we say simply that \(f\) is of exponential order.

The next theorem gives useful sufficient conditions for a function \(f\) to have a Laplace transform. The proof is sketched in Exercise 8.1.10.

Theorem 7.1.6

If \(f\) is piecewise continuous on \([0,\infty)\) and of exponential order \(s_0,\) then \({\cal L}(f)\) is defined for \(s>s_0\).

Note

We emphasize that the conditions of Theorem 7.1.6 are sufficient, but not necessary, for \(f\) to have a Laplace transform. For example, Exercise 8.1.14(c) shows that \(f\) may have a Laplace transform even though \(f\) isn’t of exponential order

Example 7.1.8

If \(f\) is bounded on some interval \([t_0,\infty)\), say

\[|f(t)|\le M,\quad t\ge t_0,\nonumber\]

then Equation \ref{eq:8.1.14} holds with \(s_0=0\), so \(f\) is of exponential order zero. Thus, for example, \(\sin\omega t\) and \(\cos \omega t\) are of exponential order zero, and Theorem 7.1.6 implies that \({\cal L}(\sin\omega t)\) and \({\cal L}(\cos \omega t)\) exist for \(s>0\). This is consistent with the conclusion of Example 7.1.4 .

Example 7.1.9

It can be shown that if \(\lim_{t\to\infty}e^{-s_0t}f(t)\) exists and is finite then \(f\) is of exponential order \(s_0\) (Exercise 8.1.9). If \(\alpha\) is any real number and \(s_0>0\) then \(f(t)=t^\alpha\) is of exponential order \(s_0\), since

\[\lim_{t\to\infty}e^{-s_0t}t^\alpha=0,\nonumber\]

by L’Hôpital’s rule. If \(\alpha\ge 0\), \(f\) is also continuous on \([0,\infty)\). Therefore Exercise 8.1.9 and Theorem 7.1.6 imply that \({\cal L}(t^\alpha)\) exists for \(s\ge s_0\). However, since \(s_0\) is an arbitrary positive number, this really implies that \({\cal L}(t^\alpha)\) exists for all \(s>0\). This is consistent with the results of Example 7.1.2 and Exercises 8.1.6 and 8.1.8.

Example 7.1.10

Find the Laplace transform of the piecewise continuous function

\[f(t)=\left\{\begin{array}{cl} 1,&0\le t<1,\\ -3e^{-t},&t\ge 1.\end{array}\right.\nonumber\]

Solution

Since \(f\) is defined by different formulas on \([0,1)\) and \([1,\infty)\), we write

\[F(s)=\int_0^\infty e^{-st} f(t)\,dt =\int_0^1e^{-st}(1)\,dt+\int_1^\infty e^{-st}(-3e^{-t})\,dt.\nonumber\]

Since

\[\int_{0}^{1}e^{-st}dt = \left\{\begin{array}{cl} {\frac{1-e^{-s}}{s}}&{s\neq 0} \\ {1}&{s=0} \end{array} \right. \nonumber \]

and

\[\int_1^\infty e^{-st}(-3e^{-t})\,dt=-3\int_1^\infty e^{-(s+1)t}\,dt=-{3e^{-(s+1)}\over s+1},\quad s>-1,\nonumber\]

it follows that

\[F(s) = \left\{\begin{array}{rl}{\frac{1-e^{-s}}{s}-3\frac{e^{-(s+1)}}{s+1}}&{s>-1, s\neq 0} \\ {1-\frac{3}{e}}&{s=0} \end{array} \right. \nonumber \]

This is consistent with Theorem 7.1.6 , since

\[|f(t)|\le 3e^{-t},\quad t\ge 1,\nonumber\]

and therefore \(f\) is of exponential order \(s_0=-1\).

Note

In Section 8.4 we’ll develop a more efficient method for finding Laplace transforms of piecewise continuous functions.

Example 7.1.11

We stated earlier that

\[\int_0^\infty e^{-st} e^{t^2} dt=\infty \nonumber\]

for all \(s\), so Theorem 7.1.6 implies that \(f(t)=e^{t^2}\) is not of exponential order, since

\[\lim_{t\to\infty} {e^{t^2}\over Me^{s_0t}}=\lim_{t\to\infty} {1\over M} e^{t^2-s_0t}=\infty, \nonumber\]

so

\[e^{t^2}>Me^{s_0t} \nonumber\]

for sufficiently large values of \(t\), for any choice of \(M\) and \(s_{0}\) (Exercise 8.1.3).