3. 10: Derivatives of Inverse Trig Functions
- Last updated
- Jun 6, 2019
- Save as PDF
- Page ID
- 20623
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section we explore the relationship between the derivative of a function and the derivative of its inverse. For functions whose derivatives we already know, we can use this relationship to find derivatives of inverses without having to use the limit definition of the derivative. In particular, we will apply the formula for derivatives of inverse functions to trigonometric functions. This formula may also be used to extend the power rule to rational exponents.
The Derivative of an Inverse Function
Note: The Inverse Function Theorem is an "extra" for our course, but can be very useful. There are other methods to derive (prove) the derivatives of the inverse Trigonmetric functions. Be sure to see the Table of Derivatives of Inverse Trigonometric Functions.
We begin by considering a function and its inverse. If f(x) is both invertible and differentiable, it seems reasonable that the inverse of f(x) is also differentiable. Figure shows the relationship between a function f(x) and its inverse f−1(x). Look at the point (a,f−1(a)) on the graph of f−1(x) having a tangent line with a slope of
(f−1)′(a)=pq.
This point corresponds to a point (f−1(a),a) on the graph of f(x) having a tangent line with a slope of
f′(f−1(a))=qp.
Thus, if f−1(x) is differentiable at a, then it must be the case that
(f−1)′(a)=1f′(f−1(a)).
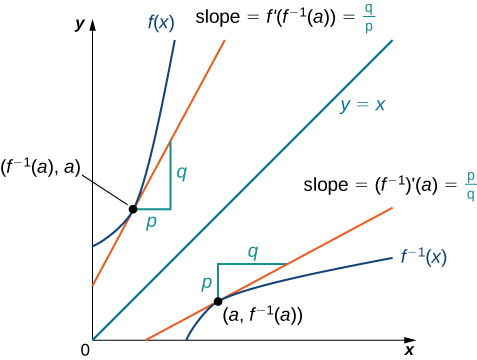
Figure 3.10.1:The tangent lines of a function and its inverse are related; so, too, are the derivatives of these functions.
We may also derive the formula for the derivative of the inverse by first recalling that x=f(f−1(x)). Then by differentiating both sides of this equation (using the chain rule on the right), we obtain
1=f′(f−1(x))(f−1)′(x)).
Solving for (f−1)′(x), we obtain
(f−1)′(x)=1f′(f−1(x)).
We summarize this result in the following theorem.
Inverse Function Theorem
Let f(x) be a function that is both invertible and differentiable. Let y=f−1(x) be the inverse of f(x). For all x satisfying f′(f−1(x))≠0,
dydx=ddx(f−1(x))=(f−1)′(x)=1f′(f−1(x)).
Alternatively, if y=g(x) is the inverse of f(x), then
g(x)=1f′(g(x)).
Example 3.10.1: Applying the Inverse Function Theorem
Use the inverse function theorem to find the derivative of g(x)=x+2x. Compare the resulting derivative to that obtained by differentiating the function directly.
Solution
The inverse of g(x)=x+2x is f(x)=2x−1.
Since g′(x)=1f′(g(x)),
begin by finding f′(x). Thus,
f′(x)=−2(x−1)2 and f′(g(x))=−2(g(x)−1)2=−2(x+2x−1)2=−x22.
Finally,
g′(x)=1f′(g(x))=−2x2.
We can verify that this is the correct derivative by applying the quotient rule to g(x) to obtain
g′(x)=−2x2.
![]() Exercise 3.10.1
Exercise 3.10.1
Use the inverse function theorem to find the derivative of g(x)=1x+2. Compare the result obtained by differentiating g(x) directly.
- Hint
-
Use the preceding example as a guide.
- Answer
-
g′(x)=−1(x+2)2
Example 3.10.2: Applying the Inverse Function Theorem
Use the inverse function theorem to find the derivative of g(x)=3√x.
Solution
The function g(x)=3√x is the inverse of the function f(x)=x3. Since g′(x)=1f′(g(x)), begin by finding f′(x). Thus,
f′(x)=3x3
and
f′(g(x))=3(3√x)2=3x2/3
Finally,
g′(x)=13x2/3=13x−2/3.
![]() Exercise 3.10.2
Exercise 3.10.2
Find the derivative of g(x)=5√x by applying the inverse function theorem.
- Hint
-
g(x) is the inverse of f(x)=x5.
- Answer
-
g(x)=15x−4/5
From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form 1n, where n is a positive integer. This extension will ultimately allow us to differentiate xq, where q is any rational number.
Extending the Power Rule to Rational Exponents
The power rule may be extended to rational exponents. That is, if n is a positive integer, then
ddx(x1/n)=1nx(1/n)−1.
Also, if n is a positive integer and m is an arbitrary integer, then
ddx(xm/n)=mnx(m/n)−1.
Proof
The function g(x)=x1/n is the inverse of the function f(x)=xn. Since g′(x)=1f′(g(x)), begin by finding f′(x). Thus,
f′(x)=nxn−1 and f′(g(x))=n(x1/n)n−1=nx(n−1)/n.
Finally,
g′(x)=1nx(n−1)/n=1nx(1−n)/n=1nx(1/n)−1.
To differentiate xm/n we must rewrite it as (x1/n)m and apply the chain rule. Thus,
ddx(xm/n)=ddx((x1/n)m)=m(x1/n)m−1⋅1nx(1/n)−1=mnx(m/n)−1.
□
Example 3.10.3: Applying the Power Rule to a Rational Power
Find the equation of the line tangent to the graph of y=x2/3 at x=8.
Solution
First find dydx and evaluate it at x=8. Since
dydx=23x−1/3 and dydx∣x=8=13
the slope of the tangent line to the graph at x=8 is 13.
Substituting x=8 into the original function, we obtain y=4. Thus, the tangent line passes through the point (8,4). Substituting into the point-slope formula for a line, we obtain the tangent line
y=13x+43.
![]() Exercise 3.10.3
Exercise 3.10.3
Find the derivative of s(t)=√2t+1.
- Hint
-
Use the chain rule.
- Answer
-
s′(t)=(2t+1)−1/2
Derivatives of Inverse Trigonometric Functions
We now turn our attention to finding derivatives of inverse trigonometric functions. These derivatives will prove invaluable in the study of integration later in this text. The derivatives of inverse trigonometric functions are quite surprising in that their derivatives are actually algebraic functions. Previously, derivatives of algebraic functions have proven to be algebraic functions and derivatives of trigonometric functions have been shown to be trigonometric functions. Here, for the first time, we see that the derivative of a function need not be of the same type as the original function.
Example 3.10.4: Derivative of the Inverse Sine Function
Use the inverse function theorem to find the derivative of g(x)=sin−1x.
Solution
Since for x in the interval [−π2,π2],f(x)=sinx is the inverse of g(x)=sin−1x, begin by finding f′(x). Since
f′(x)=cosx and f′(g(x))=cos(sin−1x)=√1−x2,
we see that
g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Analysis
To see that cos(sin−1x)=√1−x2, consider the following argument. Set sin−1x=θ. In this case, sinθ=x where −π2≤θ≤π2. We begin by considering the case where 0<θ<π2. Since θ is an acute angle, we may construct a right triangle having acute angle θ, a hypotenuse of length 1 and the side opposite angle θ having length x. From the Pythagorean theorem, the side adjacent to angle θ has length √1−x2. This triangle is shown in Figure. Using the triangle, we see that cos(sin−1x)=cosθ=√1−x2.
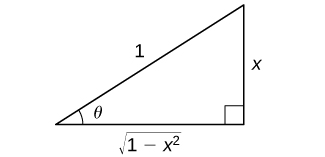
Figure 3.10.2: Using a right triangle having acute angle θ, a hypotenuse of length 1, and the side opposite angle θ having length x, we can see that cos(sin−1x)=cosθ=√1−x2.
In the case where −π2<θ<0, we make the observation that 0<−θ<π2 and hence
cos(sin−1x)=cosθ=cos(−θ)=√1−x2.
Now if θ=π2 or θ=−π2,x=1 or x=−1, and since in either case cosθ=0 and √1−x2=0, we have
cos(sin−1x)=cosθ=√1−x2.
Consequently, in all cases, cos(sin−1x)=√1−x2.
Example 3.10.5: Applying the Chain Rule to the Inverse Sine Function
Apply the chain rule to the formula derived in Example to find the derivative of h(x)=sin−1(g(x)) and use this result to find the derivative of h(x)=sin−1(2x3).
Solution
Applying the chain rule to h(x)=sin−1(g(x)), we have
h′(x)=1√1−(g(x))2g′(x).
Now let g(x)=2x3, so g′(x)=6x. Substituting into the previous result, we obtain
h′(x)=1√1−4x6⋅6x=6x√1−4x6
![]() Exercise 3.10.4
Exercise 3.10.4
Use the inverse function theorem to find the "derive" the derivative of g(x)=tan−1x.
- Hint
-
The inverse of g(x) is f(x)=tanx. Use Example 3.10.5 as a guide.
- Answer
-
g′(x)=11+x2
The derivatives of the remaining inverse trigonometric functions may also be found by using the inverse function theorem. These formulas are provided in the following theorem.
Table of Derivatives of Inverse Trigonometric Functions
ddxsin−1x=1√1−(x)2
ddxcos−1x=−1√1−(x)2
ddxtan−1x=11+(x)2
ddxcot−1x=−11+(x)2
ddxsec−1x=1|x|√(x)2−1
ddxcsc−1x=−1|x|√(x)2−1
Example 3.10.6: Applying Differentiation Formulas to an Inverse Tangent Function
Find the derivative of f(x)=tan−1(x2).
Solution
Letg(x)=x2, so g′(x)=2x. Substituting into Equation, we obtain
f′(x)=11+(x2)2⋅(2x).
Simplifying, we have
f′(x)=2x1+x4.
Example 3.10.7: Applying Differentiation Formulas to an Inverse Sine Function
Find the derivative of h(x)=x2sin−1x.
Solution
By applying the product rule, we have
h′(x)=2xsin−1x+1√1−x2⋅x2
![]() Exercise 3.10.5
Exercise 3.10.5
Find the derivative of h(x)=cos−1(3x−1).
- Hint
-
Use Equation. with g(x)=3x−1
- Answer
-
h′(x)=−3√6x−9x2
Example 3.10.8: Applying the Inverse Tangent Function
The position of a particle at time t is given by s(t)=tan−1(1t) for t≥12. Find the velocity of the particle at time t=1.
Solution
Begin by differentiating s(t) in order to find v(t).Thus,
v(t)=s′(t)=11+(1t)2⋅−1t2.
Simplifying, we have
v(t)=−1t2+1.
Thus, v(1)=−12.
![]() Exercise 3.10.6
Exercise 3.10.6
Find the equation of the line tangent to the graph of f(x)=sin−1x at x=0.
- Hint
-
f′(0) is the slope of the tangent line.
- Answer
-
y=x
Key Concepts
- The inverse function theorem allows us to compute derivatives of inverse functions without using the limit definition of the derivative.
- We can use the inverse function theorem to develop differentiation formulas for the inverse trigonometric functions.
Key Equations
- Inverse function theorem
(f−1)′(x)=1f′(f−1(x)) whenever f′(f−1(x))≠0 and f(x) is differentiable.
- Power rule with rational exponents
ddx(xm/n)=mnx(m/n)−1.
- Derivative of inverse sine function
ddxsin−1x=1√1−(x)2
- Derivative of inverse cosine function
ddxcos−1x=−1√1−(x)2
Derivative of inverse tangent function
ddxtan−1x=11+(x)2
Derivative of inverse cotangent function
ddxcot−1x=−11+(x)2
Derivative of inverse secant function
ddxsec−1x=1√|x|(x)2−1
Derivative of inverse cosecant function
ddxcsc−1x=−1|x|√(x)2−1
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

