10.7: Predicting the Shapes of Molecules
- Page ID
- 25815
- Determine the shape of simple molecules.
Molecules have shapes. There is an abundance of experimental evidence to that effect—from their physical properties to their chemical reactivity. Small molecules—molecules with a single central atom—have shapes that can be easily predicted. The basic idea in molecular shapes is called valence shell electron pair repulsion (VSEPR). VSEPR says that electron pairs, being composed of negatively charged particles, repel each other to get as far away from one another as possible. VSEPR makes a distinction between electron group geometry, which expresses how electron groups (bonds and nonbonding electron pairs) are arranged, and molecular geometry, which expresses how the atoms in a molecule are arranged. However, the two geometries are related.
There are two types of electron groups: any type of bond—single, double, or triple—and lone electron pairs. When applying VSEPR to simple molecules, the first thing to do is to count the number of electron groups around the central atom. Remember that a multiple bond counts as only one electron group.
Any molecule with only two atoms is linear. A molecule whose central atom contains only two electron groups orients those two groups as far apart from each other as possible—180° apart. When the two electron groups are 180° apart, the atoms attached to those electron groups are also 180° apart, so the overall molecular shape is linear. Examples include BeH2 and CO2:
 Figure \(\PageIndex{1}\): Beryllium hydride and carbon dioxide bonding.
Figure \(\PageIndex{1}\): Beryllium hydride and carbon dioxide bonding.
The two molecules, shown in the figure below in a "ball and stick" model.
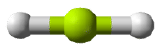
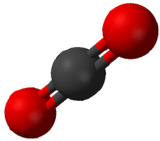 Figure \(\PageIndex{2}\): Beryllium hydride and carbon dioxide models. (CK12 Licence)
Figure \(\PageIndex{2}\): Beryllium hydride and carbon dioxide models. (CK12 Licence)
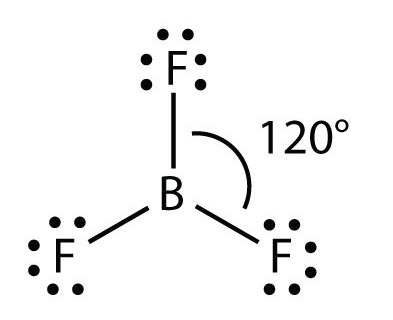
A molecule with three electron groups orients the three groups as far apart as possible. They adopt the positions of an equilateral triangle—120° apart and in a plane. The shape of such molecules is trigonal planar. An example is BF3:
Some substances have a trigonal planar electron group distribution but have atoms bonded to only two of the three electron groups. An example is GeF2:
 Figure \(\PageIndex{4}\): Germanium difluoride bonding.
Figure \(\PageIndex{4}\): Germanium difluoride bonding.
From an electron group geometry perspective, GeF2 has a trigonal planar shape, but its real shape is dictated by the positions of the atoms. This shape is called bent or angular.
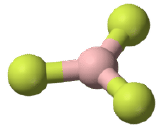
A molecule with four electron groups about the central atom orients the four groups in the direction of a tetrahedron, as shown in Figure \(\PageIndex{1}\) Tetrahedral Geometry. If there are four atoms attached to these electron groups, then the molecular shape is also tetrahedral. Methane (CH4) is an example.
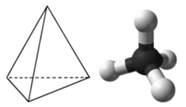 Figure \(\PageIndex{5}\): Tetrahedral structure of methane. (CK12 Licence)
Figure \(\PageIndex{5}\): Tetrahedral structure of methane. (CK12 Licence)
This diagram of CH4 illustrates the standard convention of displaying a three-dimensional molecule on a two-dimensional surface. The straight lines are in the plane of the page, the solid wedged line is coming out of the plane toward the reader, and the dashed wedged line is going out of the plane away from the reader.
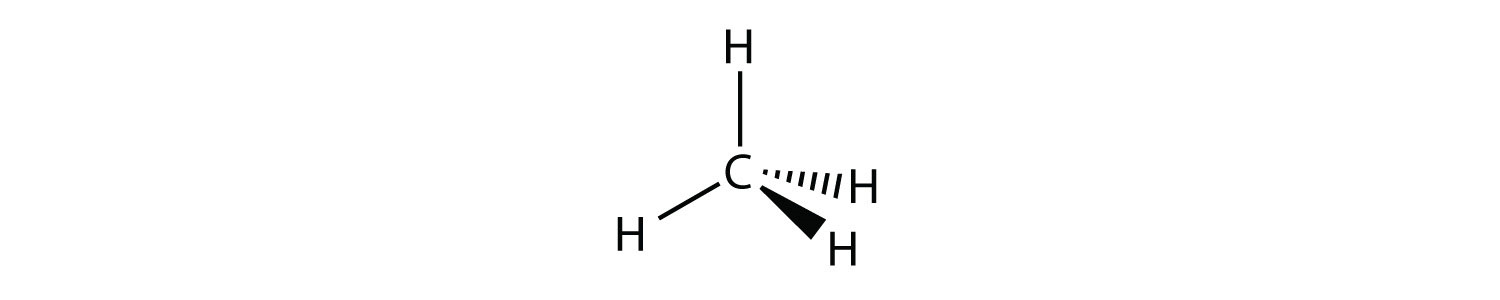 Figure \(\PageIndex{6}\): Methane bonding. (CK12 Licence)
Figure \(\PageIndex{6}\): Methane bonding. (CK12 Licence)
NH3 is an example of a molecule whose central atom has four electron groups, but only three of them are bonded to surrounding atoms.
 Figure \(\PageIndex{7}\): Ammonia bonding. (CK12 Licence)
Figure \(\PageIndex{7}\): Ammonia bonding. (CK12 Licence)
Although the electron groups are oriented in the shape of a tetrahedron, from a molecular geometry perspective, the shape of NH3 is trigonal pyramidal.
H2O is an example of a molecule whose central atom has four electron groups, but only two of them are bonded to surrounding atoms.
 Figure \(\PageIndex{8}\): Water bonding.
Figure \(\PageIndex{8}\): Water bonding.
Although the electron groups are oriented in the shape of a tetrahedron, the shape of the molecule is bent or angular. A molecule with four electron groups about the central atom, but only one electron group bonded to another atom, is linear because there are only two atoms in the molecule.
Double or triple bonds count as a single electron group. The Lewis electron dot diagram of formaldehyde (CH2O) is shown in Figure \(\PageIndex{9}\).
 Figure \(\PageIndex{9}\): Lewis Electron Dot Diagram of Formaldehyde.
Figure \(\PageIndex{9}\): Lewis Electron Dot Diagram of Formaldehyde.
The central C atom has three electron groups around it because the double bond counts as one electron group. The three electron groups repel each other to adopt a trigonal planar shape.
 Figure \(\PageIndex{10}\): Formaldehyde bonding.
Figure \(\PageIndex{10}\): Formaldehyde bonding.
(The lone electron pairs on the O atom are omitted for clarity.) The molecule will not be a perfect equilateral triangle because the C–O double bond is different from the two C–H bonds, but both planar and triangular describe the appropriate approximate shape of this molecule.
Table \(\PageIndex{1}\) summarizes the shapes of molecules based on the number of electron groups and surrounding atoms.
| Number of Electron Groups on Central Atom | Number of Bonding Groups | Number of Lone Pairs | Electron Geometry | Molecular Shape |
|---|---|---|---|---|
| 2 | 2 | 0 | linear | linear |
| 3 | 3 | 0 | trigonal planar | trigonal planar |
| 3 | 2 | 1 | trigonal planar | bent |
| 4 | 4 | 0 | tetrahedral | tetrahedral |
| 4 | 3 | 1 | tetrahedral | trigonal pyramidal |
| 4 | 2 | 2 | tetrahedral | bent |
What is the approximate shape of each molecule?
- PCl3
- NOF
Solution
The first step is to draw the Lewis structure of the molecule.
For \(\ce{PCl3}\), the electron dot diagram is as follows:
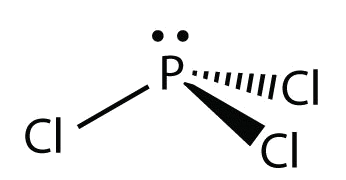
The lone electron pairs on the Cl atoms are omitted for clarity. The P atom has four electron groups with three of them bonded to surrounding atoms, so the molecular shape is trigonal pyramidal.
The electron dot diagram for \(\ce{NOF}\) is as follows:
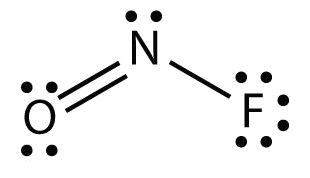
The N atom has three electron groups on it, two of which are bonded to other atoms. The molecular shape is bent.
What is the approximate molecular shape of \(\ce{CH2Cl2}\)?
- Answer
-
Tetrahedral
Ethylene (\(\ce{C2H4}\)) has two central atoms. Determine the geometry around each central atom and the shape of the overall molecule. (Hint: hydrogen is a terminal atom.)
- Answer
-
Trigonal planar about both central C atoms.
Summary
The approximate shape of a molecule can be predicted from the number of electron groups and the number of surrounding atoms.

