12.2E: Exercises for Section 12.2
- Last updated
- Jan 6, 2020
- Save as PDF
- Page ID
- 30610
( \newcommand{\kernel}{\mathrm{null}\,}\)
Taking Derivatives of Vector-Valued Functions
In questions 1 - 10, compute the derivative of each vector-valued function.
1) ⇀r(t)=t3ˆi+3t2ˆj+t36ˆk
- Answer
- ⇀r′(t)=3t2ˆi+6tˆj+12t2ˆk
2) ⇀r(t)=sin(t)ˆi+cos(t)ˆj+etˆk
3) ⇀r(t)=e−tˆi+sin(3t)ˆj+10√tˆk. A sketch of the graph is shown here. Notice the varying periodic nature of the graph.
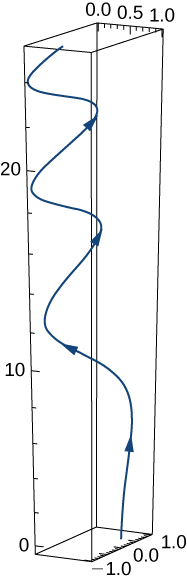
- Answer
- ⇀r′(t)=−e−tˆi+3cos(3t)ˆj+5√tˆk
4) ⇀r(t)=etˆi+2etˆj+ˆk
5) ⇀r(t)=ˆi+ˆj+ˆk
- Answer
- ⇀r′(t)=⟨0,0,0⟩=⇀0
6) ⇀r(t)=tetˆi+tln(t)ˆj+sin(3t)ˆk
7) ⇀r(t)=⟨1t+1,arctan(t),lnt3⟩
- Answer
- ⇀r′(t)=⟨−1(t+1)2,11+t2,3t⟩
8) ⇀r(t)=⟨tan2t,sec2t,sin2t⟩
9) ⇀r(t)=⟨3,4sin(3t),tcos(t)⟩
- Answer
- ⇀r′(t)=⟨0,12cos(3t),cost−tsint⟩
10) ⇀r(t)=t2ˆi+te−2tˆj−5e−4tˆk
11) a. Describe and sketch the curve represented by the vector-valued function ⇀r(t)=⟨6t,6t−t2⟩.
b. Locate the highest point on the curve ⇀r(t)=⟨6t,6t−t2⟩ and give the value of the function at this point.
- Answer
- b. ⇀r(t)=⟨18,9⟩ at t=3
12) Find the parametric equations of the tangent line to the curve ⇀r(t)=⟨t,t2,t⟩ at t=2.
13) Find the parametric equations of the tangent line to the curve ⇀r(t)=⟨et,e−t,0⟩ at t=0.
- Answer
- x=1+t,y=1−t,z=0
14) Compute the first, second, and third derivatives of ⇀r(t)=3tˆi+6ln(t)ˆj+5e−3tˆk.
Describing Motion with Vector-Valued Functions
In questions 15 - 17, find the velocity and acceleration at the given times, plot the graph of the position function, and draw in the velocity and acceleration vectors at the corresponding locations on the curve.
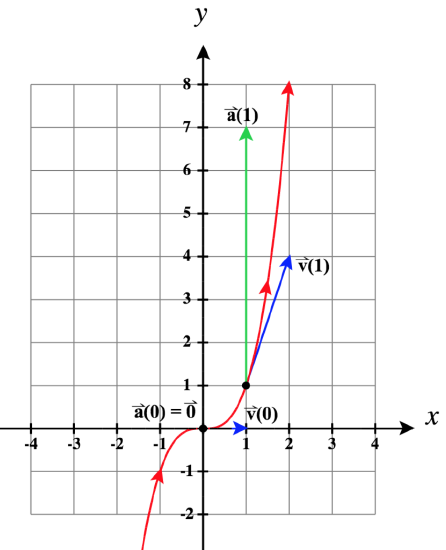
15) ⇀r(t)=tˆi+t3ˆj, at t=0 and at t=1
- Answer
- t=0:t=1:⇀r(t)=tˆi+t3ˆj,⇀r(0)=⇀0,⇀r(1)=ˆi+ˆj⇀v(t)=ˆi+3t2ˆj,⇀v(0)=ˆi,⇀v(1)=ˆi+3ˆj⇀a(t)=6tˆj,⇀a(0)=⇀0,⇀a(1)=6ˆj
16) ⇀r(t)=costˆi+sin3tˆj, at t=0, at t=π4, and at t=π2
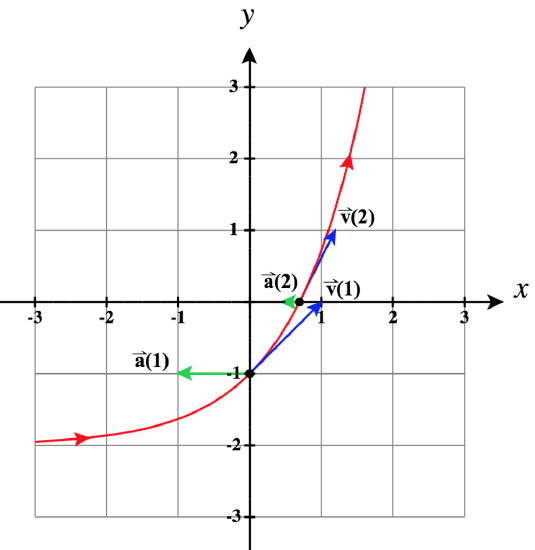
17) ⇀r(t)=lntˆi+(t−2)ˆj, at t=1 and at t=2
- Answer
- t=1:t=2:⇀r(t)=(lnt)ˆi+(t−2)ˆj,⇀r(1)=−ˆj,⇀r(2)=(ln2)ˆi⇀v(t)=1tˆi+ˆj,⇀v(1)=ˆi+ˆj,⇀v(2)=12ˆi+ˆj⇀a(t)=−1t2ˆi,⇀a(1)=−ˆi,⇀a(2)=−14ˆi
In questions 18 - 24, find the velocity, speed, and acceleration of a particle with the given position function. Remember that the speed is the magnitude of the velocity represented by ‖⇀v(t)‖ or ‖⇀r′(t)‖.
18) ⇀r(t)=e2tˆi+sintˆj
19) ⇀r(t)=cost3ˆi+sint3ˆj
- Answer
- ⇀v(t)=−3t2sint3ˆi+3t2cost3ˆj,speed(t)=‖⇀v(t)‖=3t2,⇀a(t)=(−6tsint3−9t4cost3)ˆi+(6tcost3−9t4sint3)ˆj
20) ⇀r(t)=⟨et,e−t,0⟩
21) ⇀r(t)=⟨t+cost,t−sint⟩
- Answer
- ⇀v(t)=⟨1−sint,1−cost⟩,speed(t)=‖⇀v(t)‖=√3−2(sint+cost),⇀a(t)=⟨−cost,sint⟩
22) ⇀r(t)=2t−12t+1ˆi+ln(1−4t2)ˆj
23) ⇀r(t)=cos3tˆi+sin3tˆj+0.5tˆk
- Answer
- ⇀v(t)=−3sin3tˆi+3cos3tˆj+0.5ˆk,speed(t)=‖⇀v(t)‖=√9.25 units/sec,⇀a(t)=−9cos3tˆi−9sin3tˆj
24) ⇀r(t)=e−tˆi+(lnt)ˆj+(sin7t)ˆk
25) Consider the position vector for a particle to be ⇀r(t)=tˆi+t2ˆj+t3ˆk. The graph is shown here:
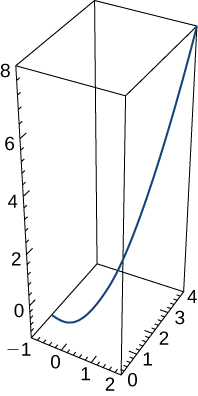
a. Find the velocity vector at any time.
b. Find the speed of the particle at time t=2 sec.
c. Find the acceleration at time t=2 sec.
- Answer
- a. ⇀v(t)=ˆi+2tˆj+3t2ˆk
b. √161 units/sec
Note that speed(t)=‖⇀v(t)‖=√12+(2t)2+(3t2)2=√1+4t2+9t4.
Hence, speed(2)=√1+16+9(16)=√161 units/sec.
c. Since ⇀a(t)=2ˆj+6tˆk, ⇀a(2)=2ˆj+12ˆk
26) A particle travels along the path of an ellipse with the equation ⇀r(t)=costˆi+2sintˆj+0ˆk. Find the following:
a. Velocity of the particle
- Answer
- ⇀v(t)=⟨−sint,2cost,0⟩
b. Speed of the particle at t=π4
c. Acceleration of the particle at t=π4
- Answer
- ⇀a(t)=⟨−√22,−√2,0⟩
27) Show that if the speed of a particle traveling along a curve represented by a vector-valued function is constant, then the velocity function is always perpendicular to the acceleration function.
- Answer
- ‖⇀v(t)‖=k⇀v(t)·⇀v(t)=k2ddt(⇀v(t)·⇀v(t))=ddt(k2)=0⇀v(t)·⇀v′(t)+⇀v′(t)·⇀v(t)=02⇀v(t)·⇀v′(t)=0⇀v(t)·⇀v′(t)=0
The last statement implies that the velocity and acceleration are perpendicular or orthogonal.
28) Given the vector-valued function ⇀r(t)=⟨tant,sect,0⟩ (graph is shown here), find the following:
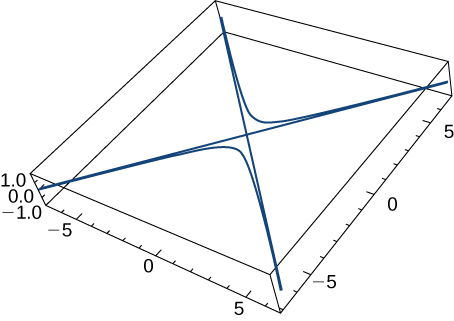
a. Velocity
- Answer
- ⇀v(t)=⟨sec2t,secttant⟩
b. Speed
- Answer
- ‖⇀v(t)‖=√sec4t+sec2ttan2t=√(sec2t)(sec2t+tan2t)
c. Acceleration
- Answer
- ⇀a(t)=⟨2sec2ttant,secttan2t+sec3t⟩
29) Find the minimum speed of a particle traveling along the curve ⇀r(t)=⟨t+cost,t−sint⟩, where t∈[0,2π). Then also find its maximum speed on this interval.
- Answer
- Min. speed is √3−2√2≈0.41421 when t=π4.
Max. speed is √3+2√2≈2.41421 when t=5π4.
For questions 30 - 31, consider a particle that moves on a circular path of radius b according to the function ⇀r(t)=bcos(ωt)ˆi+bsin(ωt)ˆj, where ω is the angular velocity, dθdt.
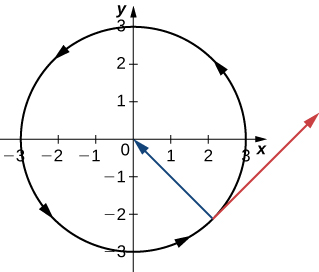
30) Show that the speed of the particle is proportional to the angular velocity.
31) Find the velocity function and show that ⇀v(t) is always orthogonal to ⇀r(t).
- Answer
- ⇀r′(t)=−bωsin(ωt)ˆi+bωcos(ωt)ˆj. To show orthogonality, note that ⇀r′(t)⋅⇀r(t)=0.
Smoothness of Vector-Valued Functions
For questions 32 - 40,
a. Determine any values of t at which ⇀r is not smooth.
b. Determine the open intervals on which ⇀r is smooth.
c. Graph the vector-valued function and describe its behavior at the points where it is not smooth.
32) ⇀r(t)=⟨3t,5t2−1⟩
33) ⇀r(t)=t3ˆi+5t2ˆj
- Answer
- a. ⇀r is not smooth at t=0, since ⇀r′(0)=⇀0.
b. ⇀r is smooth on the open intervals (−∞,0) and (0,∞).
c. There is a cusp when t=0.
34) ⇀r(t)=⟨5,2sin(t),cos(t)⟩
35) ⇀r(t)=⟨t3−3t2,7⟩
- Answer
- a. ⇀r is not smooth at t=0 and t=2, since ⇀r′(0)=⇀0 and ⇀r′(2)=⇀0.
b. ⇀r is smooth on the open intervals (−∞,0), (0,2), and (2,∞).
c. The motion on the curve reverses along the same path at both t=0 and t=2.
36) ⇀r(t)=t2ˆi+t3ˆj−5e−4tˆk
37) ⇀r(t)=⟨ln(t2+4t+5),t33−4t,5⟩
- Answer
- a. ⇀r is not smooth at t=−2, since ⇀r′(−2)=⇀0.
Since the domain of ⇀r is (−∞,∞), this is all we have to remove.
b. ⇀r is smooth on the open intervals (−∞,−2) and (−2,∞).
c. There is a cusp when t=−2.
38) ⇀r(t)=(5cost−cos5t)ˆi+(5sint−sin5t)ˆj, for 0≤t≤2π
39) ⇀r(t)=√t3+9t2ˆi+(t2+12t)ˆj+7ˆk
- Answer
- a. The domain of ⇀r is [−9,∞).
And ⇀r is not smooth at t=−6, since ⇀r′(−6)=⇀0.
The domain of ⇀r′ is (−9,∞), since ⇀r′ is undefined at t=−9.
b. ⇀r is smooth on the open intervals (−9,−6) and (−6,∞).
c. There is a cusp when t=−6.
40) ⇀r(t)=cos3tˆi+sintˆj, for 0≤t≤2π
- Answer
- a. The domain of ⇀r is (−∞,∞).
⇀r′(t)=−3(cos2t)(sint)ˆi+costˆj. It's domain is also (−∞,∞).
But note that both components have a factor of cost, so both components will be 0 when cost=0.
Therefore, ⇀r is not smooth at t=π2 and at t=3π2, since ⇀r′(π2)=⇀0 and ⇀r′(3π2)=⇀0. Note then that ⇀r is not smooth for any odd multiple of π2, that is for t=(2n+1)π2, for any integer value n.
b. ⇀r is smooth on the open intervals ((2n−1)π2,(2n+1)π2), for any integer value n.
c. There is a cusp when t=(2n+1)π2, for any integer value n.
Properties of the Derivative
For questions, 41 - 43, evaluate each expression given that ⇀r(t)=tˆi+t2ˆj−t4ˆk and ⇀s(t)=sin(t)ˆi+etˆj+cos(t)ˆk
41) ddt[⇀r(t2)]
- Answer
- ddt[⇀r(t2)]=⟨2t,4t3,−8t7⟩
42) ddt[t2⋅⇀s(t)]
43) ddt[⇀r(t)⋅⇀s(t)]
- Answer
- ddt[⇀r(t)⋅⇀s(t)]=sint+2tet−4t3cost+tcost+t2et+t4sint
44) Find ⇀r′(t)⋅⇀r″(t)for⇀r(t)=−3t5ˆi+5tˆj+2t2ˆk.
- Answer
- ⇀r′(t)⋅⇀r″(t)=900t7+16t
45) Given ⇀r(t)=tˆi+3tˆj+t2ˆk and ⇀u(t)=4tˆi+t2ˆj+t3ˆk, find ddt(⇀r(t)×⇀u(t)).
46) Evaluate ddt[⇀u(t)×⇀u′(t)] given ⇀u(t)=t2ˆi−2tˆj+ˆk.
- Answer
- ddt[⇀u(t)×⇀u′(t)]=0ˆi+2ˆj+4tˆk
47) Given ⇀r(t)=tˆi+2sintˆj+2costˆk and ⇀u(t)=1tˆi+2sintˆj+2costˆk, find the following:
a. ⇀r(t)×⇀u(t)
- Answer
- ⇀r(t)×⇀u(t)=⟨0,2(cost)(1t−t),2(sint)(t−1t)⟩
b. ddt(⇀r(t)×⇀u(t))
- Answer
- ddt(⇀r(t)×⇀u(t))=⟨0,2(sint)(t−1t)−2(cost)(1+1t2),2(sint)(1+1t2)+2(cost)(t−1t)⟩
c. Now, use the product rule for the derivative of the cross product of two vectors and show this result is the same as the answer for the preceding problem.
Unit Tangent Vectors
For questions 48 - 51, find a unit tangent vector at the indicated value of t.
48) ⇀r(t)=3t3ˆi+2t2ˆj+1tˆk;t=1
49) ⇀r(t)=tˆi+sin(2t)ˆj+cos(3t)ˆk;t=π3
- Answer
- ⇀r′(π3)=⟨1,−1,0⟩ is a tangent vector, so a unit tangent vector would be:
1√2⟨1,−1,0⟩=⟨√22,−√22,0⟩
50) ⇀r(t)=cos(2t)ˆi+2sintˆj+t2ˆk;t=π2
51) ⇀r(t)=3etˆi+2e−3tˆj+4e2tˆk;t=ln(2)
- Answer
- ⇀r′(ln(2))=⟨6,−34,32⟩ is a tangent vector, so a unit tangent vector would be:
1√1060.5625⟨6,−34,32⟩=⟨24√1696916969,−12√1696967876,128√1696916969⟩
For questions 52 - 58, find the unit tangent vector ⇀T(t) for the following parameterized curves.
52) ⇀r(t)=tˆi+3tˆj+t2ˆk
53) ⇀r(t)=6ˆi+cos(3t)ˆj+3sin(4t)ˆk,0≤t<2π
- Answer
- ⇀T(t)=1√9sin2(3t)+144cos2(4t)⟨0,−3sin(3t),12cos(4t)⟩
54) ⇀r(t)=⟨tcost,tsint⟩
55) ⇀r(t)=⟨t+1,2t+1,2t+2⟩
- Answer
- ⇀T(t)=13⟨1,2,2⟩
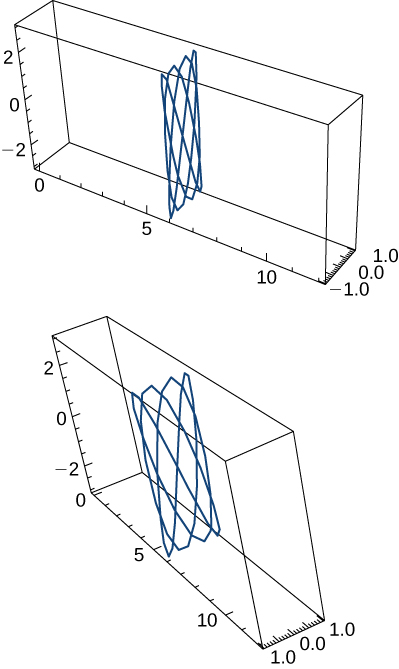
56) ⇀r(t)=costˆi+sintˆj+sintˆk,0≤t<2π. Two views of this curve are presented here:
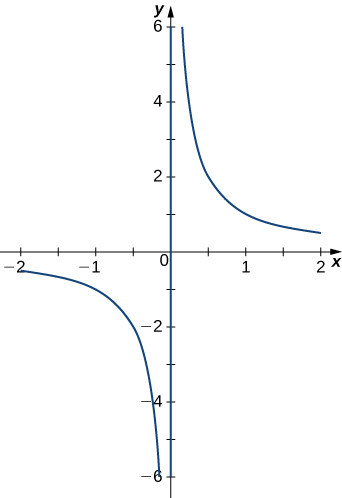
57) ⇀r(t)=⟨t,1t⟩. The graph is shown here:
- Answer
- ⇀T(t)=⟨t2√t4+1,−1√t4+1⟩
58) ⇀r(t)=3cos(4t)ˆi+3sin(4t)ˆj+5tˆk,1≤t≤2
- Answer
- ⇀T(t)=−1213sin(4t)ˆi+1213cos(4t)ˆj+513ˆk
59) A particle travels along the path of a helix with the equation ⇀r(t)=cos(t)ˆi+sin(t)ˆj+tˆk. See the graph presented here:
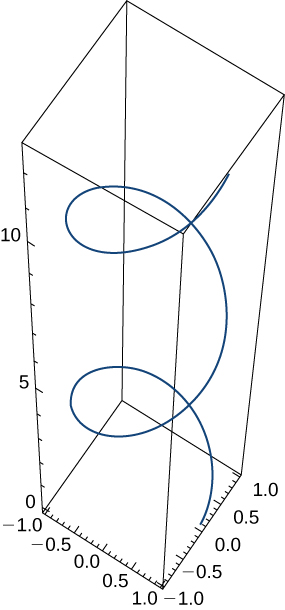
Find the following:
a. Velocity of the particle at any time
- Answer
- ⇀v(t)=⟨−sint,cost,1⟩
b. Speed of the particle at any time
c. Acceleration of the particle at any time
- Answer
- ⇀a(t)=−costˆi−sintˆj+0ˆk
d. Find the unit tangent vector for the helix.
Integration of Vector-Valued Functions
Evaluate the following integrals:
60) ∫(etˆi+sintˆj+12t−1ˆk)dt
61) ∫10⇀r(t)dt, where ⇀r(t)=⟨3√t,1t+1,e−t⟩
- Answer
- 34ˆi+ln(2)ˆj+(1−1e)ˆk
62) Evaluate ∫30‖tˆi+t2ˆj‖dt.
- Answer
- 13(1032−1)
63) The acceleration function, initial velocity, and initial position of a particle are
⇀a(t)=−5costˆi−5sintˆj,⇀v(0)=9ˆi+2ˆj,and⇀r(0)=5ˆi
Find ⇀v(t) and ⇀r(t).
- Answer
- ⇀v(t)=(9−5sint)ˆi+(−3+5cost)ˆj
⇀r(t)=(9t+5cost)ˆi+(−3t+5sint)ˆj
64) Find the antiderivative of ⇀r′(t)=cos(2t)ˆi−2sintˆj+11+t2ˆk that satisfies the initial condition ⇀r(0)=3ˆi−2ˆj+ˆk.
65) An object starts from rest at point P(1,2,0) and moves with an acceleration of ⇀a(t)=ˆj+2ˆk, where ‖⇀a(t)‖ is measured in feet per second per second. Find the location of the object after t=2 sec.
Contributors:
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Paul Seeburger (Monroe Community College) created questions 11 - 19.

