2.3E: Exercises
- Page ID
- 30365
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Solve Equations with Constants on Both Sides
In the following exercises, solve the following equations with constants on both sides.
Exercise 2.3E.1
9x−3=60
Exercise 2.3E.2
12x−8=64
- Answer
-
x=6
Exercise 2.3E.3
14w+5=117
Exercise 2.3E.4
15y+7=97
- Answer
-
y=6
Exercise 2.3E.5
2a+8=−28
Exercise 2.3E.6
3m+9=−15
- Answer
-
m=−8
Exercise 2.3E.7
−62=8n−6
Exercise 2.3E.8
−77=9b−5
- Answer
-
b=−8
Exercise 2.3E.9
35=−13y+9
Exercise 2.3E.10
60=−21x−24
- Answer
-
x=−4
Exercise 2.3E.11
−12p−9=9
Exercise 2.3E.12
−14q−2=16
- Answer
-
q=−97
Solve Equations with Variables on Both Sides
In the following exercises, solve the following equations with variables on both sides.
Exercise 2.3E.13
19z=18z−7
Exercise 2.3E.14
21k=20k−11
- Answer
-
k=−11
Exercise 2.3E.15
9x+36=15x
Exercise 2.3E.16
8x+27=11x
- Answer
-
x=9
Exercise 2.3E.17
c=−3c−20
Exercise 2.3E.18
b=−4b−15
- Answer
-
b=−3
Exercise 2.3E.19
9q=44−2q
Exercise 2.3E.20
5z=39−8z
- Answer
-
z=3
Exercise 2.3E.21
6y+12=5y
Exercise 2.3E.22
4x+34=3x
- Answer
-
x=−34
Exercise 2.3E.23
−18a−8=−22a
Exercise 2.3E.24
−11r−8=−7r
- Answer
-
r=−2
Solve Equations with Variables and Constants on Both Sides
In the following exercises, solve the following equations with variables and constants on both sides.
Exercise 2.3E.25
8x−15=7x+3
Exercise 2.3E.26
6x−17=5x+2
- Answer
-
x=19
Exercise 2.3E.27
26+13d=14d+11
Exercise 2.3E.28
21+18f=19f+14
- Answer
-
f=7
Exercise 2.3E.29
2p−1=4p−33
Exercise 2.3E.30
12q−5=9q−20
- Answer
-
q=−5
Exercise 2.3E.31
4a+5=−a−40
Exercise 2.3E.32
8c+7=−3c−37
- Answer
-
c=−4
Exercise 2.3E.33
5y−30=−5y+30
Exercise 2.3E.34
7x−17=−8x+13
- Answer
-
x=2
Exercise 2.3E.35
7s+12=5+4s
Exercise 2.3E.36
9p+14=6+4p
- Answer
-
p=−85
Exercise 2.3E.37
2z−6=23−z
Exercise 2.3E.38
3y−4=12−y
- Answer
-
y=4
Exercise 2.3E.39
53c−3=23c−16
Exercise 2.3E.40
74m−7=34m−13
- Answer
-
m=−6
Exercise 2.3E.41
8−25q=35q+6
Exercise 2.3E.42
11−15a=45a+4
- Answer
-
a=7
Exercise 2.3E.43
43n+9=13n−9
Exercise 2.3E.44
54a+15=34a−5
- Answer
-
a=−40
Exercise 2.3E.45
14y+7=34y−3
Exercise 2.3E.46
35p+2=45p−1
- Answer
-
p=15
Exercise 2.3E.47
14n+8.25=9n+19.60
Exercise 2.3E.48
13z+6.45=8z+23.75
- Answer
-
z=3.46
Exercise 2.3E.49
2.4w−100=0.8w+28
Exercise 2.3E.50
2.7w−80=1.2w+10
- Answer
-
w=60
Exercise 2.3E.51
5.6r+13.1=3.5r+57.2
Exercise 2.3E.52
6.6x−18.9=3.4x+54.7
- Answer
-
x=23
Everyday Math
Exercise 2.3E.53
Concert tickets At a school concert the total value of tickets sold was $1506. Student tickets sold for $6 and adult tickets sold for $9. The number of adult tickets sold was 5 less than 3 times the number of student tickets. Find the number of student tickets sold, s, by solving the equation 6s+27s−45=1506. Add exercises text here.
Exercise 2.3E.54
Making a fence Jovani has 150 feet of fencing to make a rectangular garden in his backyard. He wants the length to be 15
feet more than the width. Find the width, w, by solving the equation 150=2w+30+2w.
- Answer
-
30 feet
Writing Exercises
Exercise 2.3E.55
Solve the equation 65y−8=15y+7 explaining all the steps of your solution as in the examples in this section.
Exercise 2.3E.56
Solve the equation 10x+14=−2x+38 explaining all the steps of your solution as in this section.
- Answer
-
x=2 Justifications will vary.
Exercise 2.3E.57
When solving an equation with variables on both sides, why is it usually better to choose the side with the larger coefficient
of x to be the "variable" side?
Exercise 2.3E.58
Is x=−2 a solution to the equation 5−2x=−4x+1? How do you know?
- Answer
-
Yes. Justifications will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
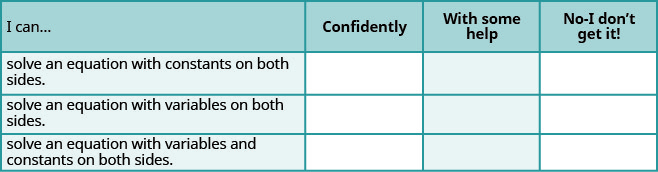
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

